Карачун В.В.,
Мельник В.М., Кривець О.О.,
Чередниченко
Д.А., Ковальчук В.В.
Національний
технічний університет України «КПІ»
ОБЧИСЛЕННЯ ПЕРЕДАТОЧНОЇ ФУНКЦІЇ ДРОТЯНОГО
ПІДВІСУ У ВИГЛЯДІ ДИСКРЕТНО НЕПЕРЕРВНОЇ МОДЕЛІ
Математична модель струнного підвісу ряду навігаційних приладів може бути
представлена у вигляді хвильового рівняння (як перше наближення) і більш повно
у вигляді рівняння динаміки важкої нитки, навантаженої одним (на вільному
кінці) або кількома вантажами.
Ці
два рівняння можуть бути зведені в одне
. (1)
Тут x,t - лінійний розмір та час, y - відхилення
точки підвісу від її положення рівноваги,
m(x), R(x) та T(x) - відповідно
маса, коефіцієнт опору рухові та натягання нитки.
Для
струни (хвильове рівняння) натягання вважається константою, а для нитки натягання
в кожній точці дорівнює сумі мас, розташованих під даною точкою, помноженій на g - прискорення земного тяжіння. 
- зовнішня
(поперечна) сила, що діє на підвіс.
Аналітичні (точні) розв’язки даної
задачі відомі, але вони надзвичайно громіздкі, щоб їх можна було
використовувати в інженерних розрахунках динаміки приладів, а, тим більше,
більш складних технічних систем. Тому представляє інтерес пошук наближеної
моделі, наприклад, у вигляді дробово-раціональної передаточної функції окремого
каналу, чи, можливо, ряду каналів в подібному об’єкті.
Для
цього динамічну модель доцільно уявляти як сукупність зосереджених мас
з’єднаних між собою невагомими нерозтяжними нитками. Відстань h між сусідніми масами
є сталою h=l/m, де l -довжина струни, m - кількість відрізків, на стиках яких розміщуються бусинки. Масу нитки
рівномірно розподіляємо між бусинками (mz=mстр/m, 1<=z<=m-1). Тут mz - маса z-ї бусинки, mстр - маса усієї струни. Бусинкам на
кінцях струни надаємо маси m0=mm=mz/2. За такої
умови сумарна маса струни буде дорівнювати сумі зосереджених мас. Якщо на
струні фіксується довільна кількість зосереджених мас будь-якої величини, то вони
додаються до відповідних мас. Остаточний розподіл мас між бусинками фіксується
масивом Mb:Coef (type Coef=array[-1..30] of real).
|
|
-1 |
0 |
1 |
2 |
3 |
... |
m |
... |
30 |
|
Mb |
m |
m0 |
m1 |
m2 |
m3 |
... |
mm |
|
|
Сили опору рухові
відтворюються масивом Mr такої ж структури як і масив Mb. На z -у бусинку діє
сила, яка дорівнює силі опору, прикладеній до відрізка підвісу довжиною h. Якщо ж на підвісі фіксовані маси з ненульовими
розмірами, то опір, викликаний наявністю цих мас, відображається відповідним
збільшенням елементів масиву Mr.
Масив T:Coef заповнюється значеннями натягання (константа для моделі струни, або як
згадувалось вище - для моделі нитки).
Дискретна модель
підвісу набуває вигляду
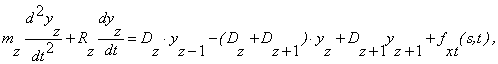(2)
.
Тут 
(далі
користуватимемось масивом D:Coef).
Граничні
умови будемо розглядати трьох родів (Ngl=1,2,3 для x=0; Ngr=1,2,3 для x=l).
Для
лівого кінця (x=0)
, (3)
де 
- переміщення
точки підвісу x=0.
, (4)
тут 
- сила, прикладена
в точці x=0.
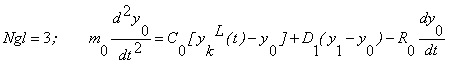, (5)
де С0 - коефіцієнт жорсткості
пружини, один кінець якої приєднано до підвісу в точці x=0, а інший переміщується на
величину 
.
Для
правого кінця (x=
)
, (6)
де 
- переміщення
точки підвісу x=l.
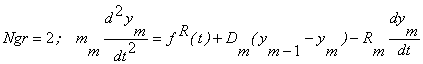, (7)
де 
- сила, що діє на
точку x=l.
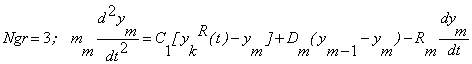, (8)
де С1 - жорсткість пружини, один
кінець якої приєднано до підвісу в точці x=l, а інший зміщується на величину 
.
Оскільки математична модель формується нами для визначення передаточної
функції будь-якого каналу, то в залежності від вибраного каналу відповідний
збурюючий чинник (вхідний сигнал) вважається присутнім. Усі ж інші приймаються
рівними нулю.
Щоб формалізувати задання вхідної
точки цікавлячої нас групи каналів, домовимось нумерувати вхідні сигнали наступним
чином:
Виконуємо
над (2) перетворення Лапласа при нульових початкових умовах та ділимо кожен
член на зображення вхідного сигналу
,
(9)
де 
,
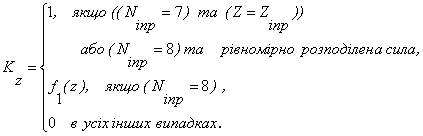
- передаточна
функція каналу «вхід з номером 
- вихід 
».
Відомо,
що в динамічних об’єктах передаточні функції усіх каналів можуть бути
представлені у вигляді
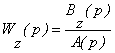, (10)
де 
- спільний для усіх передаточних функцій даного об’єкта
знаменник (характеристичний поліном об’єкта).
Множимо
(9) на A(p) і одержуємо -
(11)
Система
(11) є тридіагональною. Для її розв’язання скористаємось методом прогонки,
особливістю якого буде те, що оперувати доведеться не з числами, а з поліномами
від 
. В процесі виконання прямого ходу будемо приводити z-е рівняння до вигляду
-
. (12)
Тоді
(z-1)-е рівняння матиме вигляд
. (13)
Множимо
(11) на 
, а (13) на 
, після чого додаємо ці рівняння:
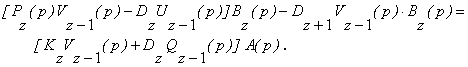(14)
Порівнюючи
(12) з (14), доходимо до висновку, що
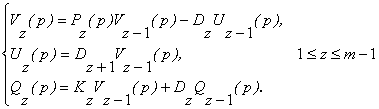. (15)
Формули
(15) можна розглядати як рекурентні. Але для того, щоб вони «запрацювали»,
необхідно з лівої граничної умови визначити
Розглянемо,
як це можна зробити. Якщо над (3) (Ngl=1) - виконати
перетворення Лапласа, поділити на зображення вхідного сигналу і помножити на A(p), то одержимо -
звідки,
порівнюючи останній вираз з (12) при z=0, можемо
прийняти
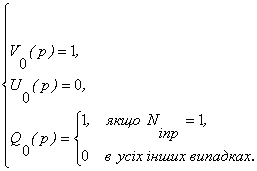(16)
Для Ngl=2 з (4) аналогічно одержуємо
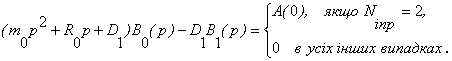
Порівнюючи
останній вираз з (12) при z=0 , приходимо
до висновку, що
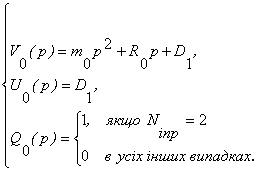(17)
При
Ngl=3 з (5) маємо
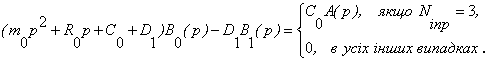
Порівнюємо
останній вираз з (12) при z=0.
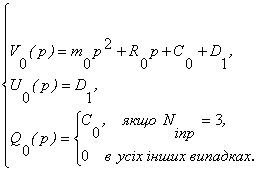(18)
Тепер
прямий хід може бути виконаний за формулами (15). При z=m-1 матимемо з (12)
. (19)
Щоб
знайти 
, доповнимо рівняння (19) граничною умовою при x=l
Ngr=1. Згідно з (6) маємо
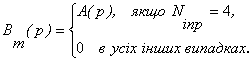(20)
Підставимо
з останнього
виразу в (19) і розв’яжемо останнє відносно 
.
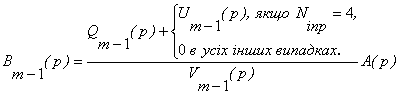Отже,
можемо прийняти, що
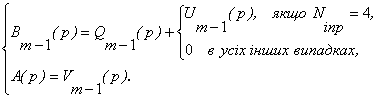(21)
Ngr=2. Згідно
з (7) одержимо
Якщо
визначити 
з останнього
виразу та підставити його в (19), то одержимо -
.
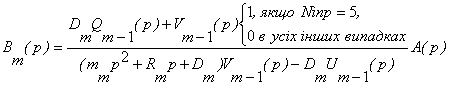Отже,
можна прийняти, що
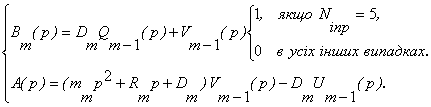(22)
Гранична
умова Ngr=3. Згідно з (8)
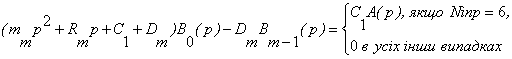
Підставляємо
з останнього
виразу в (19), звідки
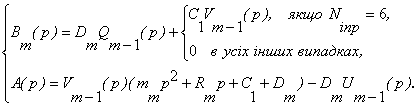
На цьому прямий хід в методі прогонки
завершується.
Зворотний хід реалізується з
використанням формули (12), яка приводиться до вигляду
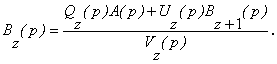
z
перебирається, починаючи з (m-2), якщо Ninp=4, або з (m-1) - в інших випадках,
завершується ж на z=0.
Оформляємо
описаний алгоритм у вигляді підпрограми WpStrNit.
Procedure WpStrNit(Mb,Mr,D:Coef;
Ninp:integer; var A:Coef; var B:Coef);
var
s,z,Zn:integer; U,V,Q,K,F,P:Coef;
begin
U[0,-1]:=0;
Q[0,-1]:=0; Q[0,0]:=0;
case Ngl of
1:begin
V[0,-1]:=0; V[0,0]:=1; U[0,0]:=0;
if Ninp=1 then Q[0,0]:=1
end;
2: begin
V[0,-1]:=2; V[0,0]:=D[1]; U[0,0]:=D[1];
V[0,1]:=Mr[0]; V[0,2]:=Mb[0];
if Ninp=2 then Q[0,0]:=1
end;
3:begin
V[0,-1]:=2; V[0,0]:=C0+D[1];
U[0,0]:=D[1];
if Ninp=3 then Q[0,0]:=C0
end
end;
for z:=1 to m-1 do
begin
P[-1]:=2;
P[0]:=D[z]+D[z+1]; P[1]:=Mr[z];
P[2]:=Mb[z]; UmnPol(P,V[z-1],P); F[-1]:=0;
F[0]:=D[z]; UmnPol(F,U[z-1],F);
AlSumPol(P,F,'-',V[z]); F[-1]:=0;
F[0]:=D[z+1];
UmnPol(F,V[z-1],U[z]);
K[-1]:=0;
K[0]:=0;
if ((Ninp=7) and (Z=Zinp)) or (Ninp=8) then
K[0]:=1;
if Ninp=8 then
K[0]:=F1[z];
F[-1]:=0;
F[0]:=D[z];
UmnPol(K,V[z-1],P); UmnPol(F,Q[z-1],F);
AlSumPol(P,F,'+',Q[z]);
end;
case Ngr of
1: begin
A:=V[m-1]; B[m]:=A; B[m-1]:=Q[m-1];
if Ninp=4 then AlSumPol(B[m-1],U[m-1],'+',B[m-1]);
end;
2:begin
F[1]:=0; F[0]:=D[m]; UmnPol(F,Q[m-1],B[m]);
if Ninp=5 then AlSumPol(B[m],V[m-1],'+',B[m]);
P[-1]:=2; P[0]:=D[m]; P[1]:=Mr[m];P[2]:=Mb[m];
UmnPol(P,V[m-1],P); F[-1]:=0; F[0]:=D[m];
UmnPol(F,U[m-1],F);
AlSumPol(P,F,'-',A)
end;
3:begin
F[-1]:=0;
F[0]:=D[m];
UmnPol(F,Q[m-1],B[m]);
if Ninp=6 then
begin
P[-1]:=0; P[0]:=C1;
UmnPol(P,V[m-1],P);
AlSumPol(B[m],P,'+',B[m])
end;
P[-1]:=2; P[0]:=D[m]+C1;
P[1]:=Mr[m];P[2]:=Mb[m];
UmnPol(P,V[m-1],A);
F[-1]:=0; F[0]:=D[m];
UmnPol(F,U[m-1],F);
AlSumPol(A,F,'-',A)
end;
end;
if
Ninp=4 then Zn:=m-2
else Zn:=m-1;
for z:=Zn downto 0 do
begin
UmnPol(Q[z],A,P);
UmnPol(U[z],B[z+1],F);
AlSumPol(P,F,'+',P); DelPol(P,V[z],B[z],F)
end;
end;
Практика
використання розглянутого алгоритму показує його безвідмовність, високу
швидкодію, зручність у користуванні. Точність апроксимації легко регулюється
величиною m .
Розглянутий
алгоритм наближеного моделювання може легко бути застосований і для інших
динамічних об’єктів з розподіленими параметрами.