Современные информационные технологии / 3. Программное обеспечение

Русакова А.

Національний технічний університет України «Київський політехнічний Інститут», м. Київ, Україна

Автоматизація прокладки шляху водорозподільних систем

Визначення оптимального шляху водопроводу це важлива частина моделювання та оптимізації водорозподільчих систем.

Уже відомі алгоритми для вирішення цієї проблеми зазвичай визначають удінственное рішення, яке в деяких випадках буде не оптимальним. Розроблено алгоритм, який базується на теорії графів які генерують все мінімальні дерева, що містять вузли в яких знаходяться споживачі, з'єднані між собою трубами і реалізований в комп'ютерній програмі для ПК. Таким чином можна визначити всі оптимальні рішення, для цього критерію. Модель оптимізації може бути застосована для розробки водорозподілення в гідроміських і гідромеліоративних системах.

Мережа водорозподілу це істотна частка всіх систем водоподачі і її вартість може досягати більше 60% всієї вартості проекту.

Слід зробити спроби знизити вартість і споживання енергії розподільчої системи за допомогою оптимізації аналізу і розробки. У деяких випадках розподільна система спочатку будується для невеликої території, яка витрачає низький потік води. Зі збільшенням водоспоживання, система збільшується. У цьому випадку спочатку представляється наявність розгалуженої мережі, яка потім трансформується в циклічну мережу зі збільшенням обсягу і безпеки. Отже, ефективна розробка розгалуженої мережі вимагає деяких оптимізаційних процесів, серед яких важливе місце займає оптимізація шляху. Ця проблема виникла і в проектуванні циклічної мережі для визначення незалежної циклічної системи (віртуальна наявність розгалуженої мережі).

Традиційно, вибір оптимального рішення здійснюється через аналітичне навчання двох з трьох версій обраних з можливого безлічі передбачених рішень. Помилки в цих рішеннях обернено пропорційні досвіду проектувальника.

Сучасні математичні дисципліни операційного дослідження дають проектувальнику величезний апарат наукового аналізу в установці оптимальних рішень.

Традиційні алгоритми оптимізації були застосовні для проблеми мінімальної вартості, наприклад в лінійному програмуванні, які вперше представив Лабье для відкритих мереж. Динамічне програмування використовується для оптимізації тимчасових процесів, наприклад в проблемах операційних систем. Стерлін і Коулбек, Коулбек, Шабель і Хельвіг і Ленс і Авумах застосували динамічне програмування для визначення оптимальних насосних операцій для мінімізації вартості в водних системах. Динамічне програмування також використовується для вирішення дерев в формі мережі і можуть бути впроваджені для вирішення циклічних систем. Також Сарбу і Валі застосували теорію графів для встановлення оптимального шляху для забезпечення води.

У напірних трубопровідних мережах спочатку вибираються вузли з водопотребителями і пристрій напору (насосна станція, резервуар), потім мережевий шлях, що з'єднує ці вузли, оптимізують за кілька кроків. Це проблема оптимізації має одне або кілька рішення. Уже відомі алгоритми (Крускала) для вирішення проблеми зазвичай визначають єдине значення з набору певних ситуацій доведених, що вони квазіоптимальні.

Розподілена мережа може бути представлена спрямованим сполученим графом G, що містить кінцеве кількість вершин (труб), з'єднаних один з одним дугами. В кінці кожної вершини є дуги з відомою кількістю енергії (вузли фіксованого класу) або зовнішнє споживання води (з'єднувальні вузли). Вода тече через вершини і може входити в граф через будь-яку дугу.

Головний критерій оптимізації, який може бути використаний:

- Мінімум затрат Σc_ij L_ij → хв

- Мінімальна довжина шляху ΣL_ij → хв

- Мінімальна робота з перевезень, транспортування ΣL_ij Q_ij → хв

- Мінімальні втрати напору Σ R_ijQ²_ij → хв

в яких L_ij, Q_ij - довжина і швидкість потоку в трубі ij (між вузлами I та j); c_ij - це специфічні витрати; R_ij - гідравлічний опір в трубі ij.

Вводиться неорієнтовний зв'язний граф G = (X, U), де X = {1,2, ..., n} представляє безліч дугових індексів і U - безліч вершин. У Кожній вершині U_ij ∈ U є асоціативне значення значення λ (uⁱ_j)> 0 в звичайних одиницях, згідно адаптованому критерієм оптимізації. Цей граф прикріплений до матриці С порядку n, елементами якої є

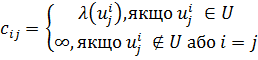
де U_ij вершина U з одним кінцем в дузі i, а іншим в дузі j.

Якщо всі значення для явні, задача має одне рішення. Якщо значення еквівалентні до декілької кількості вершин, задача має кілька рішень.

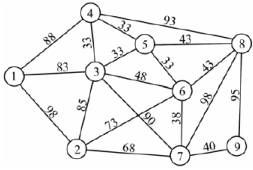
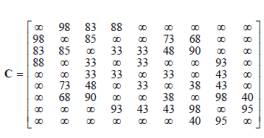
мал 1 мал 2

Для прикладу, на мал.1 зображено граф G, який прикріплено до матриці С, зображеної на мал.2. Використовуючи програму, яка базується на вищенаведеному алгоритмі отримаємо наступні результати:

· Кількість мінімальних дерев n_a = 2

· Матриця М оптимальних дуг та відповідних значень мал 3 мал 3

· Матриця А, рядки якої містять індекси для стопців впорядкованої матриці М. мал 4

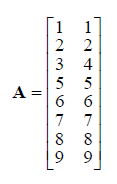
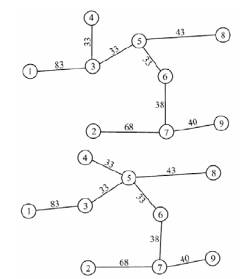
· Граф оптимального шляху, з застосуванням критерія витрат мал 5.

мал. 4

Мал. 5

Література

1. I.Sarbu, E.S.Valea. Optimization of water distribution networks path / I.Sarbu // ARPN Journal of Engineering and Applied Sciences

2. Эгильский И.С. Автоматизированные системы управления процессами подачи и распределения воды. – Л.Стройиздат,1988. – 216с