Є.О.Бойко, Д.В.Чернетченко
Дніпропетровський
національний університет ім.. Олеся Гончара
Алгоритм Дейкстри – алгоритм
на графах, винайдений недирландським вченим Е.Дейкстрой у 1959 році. Знаходить
коротшу відстань від однієї вершини графа до всіх інших. Алгоритм дійсний
тільки для графів у яких ребра не є від’ємними. Оскільки в багатьох задачах ця
умова виконується, таке обмеження не знижує популярності алгоритму Дейкстри.
Наприклад його використовує протокол OSPF для видалення кільцевих маршрутів,
також його можна застосовувати при складанні маршрутів транспортної системи як
міст так і цілих країн, тощо.
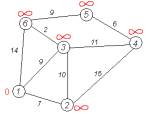
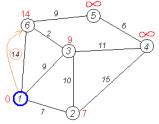
Крок 1
Відстань до
усіх вершин, окрім першої, призначаємо значення нескінченності:
|
|
|
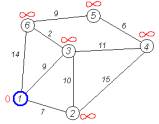
Крок 2 Знаходимо таку
вершину (із ще не оброблених), поточна найкоротша відстань до якої
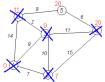
мінімальна. В нашому випадку це вершина 1. Обходимо всіх її сусідів і, якщо
шлях в сусідню вершину через 1 менший за поточний мінімальний шлях в цю
сусідню вершину, то запам'ятовуємо цей новий, коротший шлях як поточний
найкоротший шлях до сусіда. (рис. 3.3) |
Рис.3.3 Крок 2 |
|
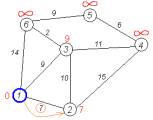
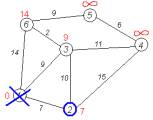
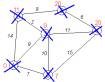
Крок 3 Перший по
порядку сусід 1-ї вершини — 2-а вершина. Шлях до неї через 1-у вершину
дорівнює найкоротшій відстані до 1-ї вершини + довжина дуги між 1-ю та 2-ю
вершиною, тобто 0 + 7 = 7. Це менше поточного найкоротшого шляху до 2-ї
вершини, тому найкоротший шлях до 2-ї вершини дорівнює 7. |
Рис. 2.4 Крок 3 |
|
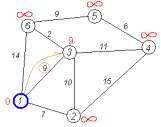
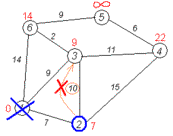
Крок 4 - 5 Аналогічну операцію проробляємо з
двома іншими сусідами 1-ї вершини — 3-ю та 6-ю. (рис. 3.5, 3.6) |
Рис. 3.5
Крок 4 |
Рис. 3.6
Крок 5 |
|
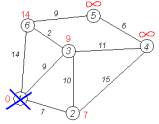
Крок 6 Всі сусіди
вершини 1 перевірені. Поточна мінімальна відстань до вершини 1 вважається
остаточною і обговоренню не підлягає (те, що це дійсно так, вперше
довів Дейкстра). Тому
викреслимо її з графа, щоб відмітити цей факт. (рис.
3.7) |
Рис. 3.7 Крок 6 |
|
|
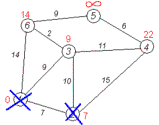
Крок 7 Практично відбувається
повернення до кроку 2. Знову знаходимо «найближчу» необроблену (не
викреслену) вершину. Це вершина 2 з поточною найкоротшою відстанню до неї =
7. І знову намагаємося зменшити відстань до всіх сусідів 2-ої
вершини, намагаючись пройти в них через 2-у. Сусідами 2-ої вершини є 1, 3, 4.
(рис. 3.8) |
Рис. 3.8 Крок 7 |
|
|
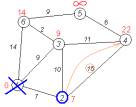
Крок 8 Перший (по порядку) сусід
вершини № 2 — 1-а вершина. Але вона вже оброблена (або
викреслена — див. крок 6). Тому з 1-ою вершиною нічого не робимо. Крок 8 (з іншими вхідними даними) Інший сусід вершини 2 — вершина 4.
Якщо йти в неї через 2-у, то шлях буде = найкоротша відстань до 2-ої +
відстань між 2-ою і 4-ою вершинами = 7 + 15 = 22. Оскільки 22 < ∞,
встановлюємо відстань до вершини № 4 рівним 22. (рис. 3.9) |
Рис. 3.9 Крок 8 |
|||
|
Крок 9 Ще один сусід
вершини 2 — вершина 3. Якщо йти в неї через 2-у, то шлях буде = 7 + 10 = 17.
Але 17 більше за відстань, що вже запам'ятали раніше до вершини № 3 і
дорівнює 9, тому поточну відстань до 3-ої вершини не міняємо. (рис.
3.10) |
Рис. 3.10 Крок 9 |
|||
|
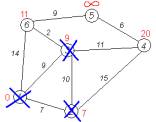
Крок 10 Всі сусіди вершини 2
переглянуті, заморожуємо відстань до неї і викреслюємо її з графа. (рис. 3.11) |
Рис. 3.11 Крок 10 |
|||
|
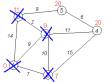
Кроки 11 — 15 По вже «відпрацьованій»
схемі повторюємо кроки 2 — 6. Тепер «найближчою» виявляється вершина № 3.
Після її «обробки» отримаємо такі результати: (рис. 3.12) |
Рис. 3.12 Крок 11-15 |
|||
|
Наступні кроки Проробляємо те саме з вершинами, що залишилися, це
вершини 6, 4 і 5 у відповідному порядку. |
Оброблення вершини 6 |
Оброблення
вершини 4 |
Оброблення вершини 5 |
|
Завершення виконання алгоритму
Алгоритм закінчує роботу, коли
викреслені всі вершини. Результат його роботи видно на останньому малюнку:
найкоротший шлях від 1-ої вершини до 2-ої становить 7, до 3-ої — 9, до
4-ої — 20, до 5-ої — 20, до 6-ої — 11 кілометрів.
Код програми
|
#include <stdio.h> main() { int G[6]; long V[6]; int E[9]; int i,j,k,y,x; printf("Vvedite
rastoyaniya meshdu gorodami\n\n"); for(i=0;i<=8;i++)
scanf("%d",&E[i]); printf("\n"); V[0]=0; for(i=1;i<=5;i++)
V[i]=100500; printf("Optimalnoe
rastoyanie do gorodov\n\n");
for(i=1,j=0;i<=3,j<=2;i++,j++) { if( (V[0]+E[j])<V[i]
) { V[i]=V[0]+E[j]; } } for(i=2,j=3,k=0,x=1;i<=4,j<=4,k<=1,x<=4;x=x+3,i=i+2,j++,k++){
if( (V[1]+E[j])<V[i]
){ V[i]= V[1]+E[j];} else V[i]=V[k]+E[x];}
for(k=0,j=2,i=3,y=5;k<=1,j<=4,i<=4,y<=6;k++,j=j+2,i++,y++){
if(
(V[2]+E[y])<V[i] ){
V[i]=V[2]+E[y];} else
V[i]=V[k]+E[j];} if(
(V[3]+E[7])<(V[4]+E[8]) ){ V[5]=V[3]+E[7];} else
V[5]=V[4]+E[8]; printf("V[2]=%d\n",V[1]);
printf("V[3]=%d\n",V[2]);
printf("V[4]=%d\n",V[4]);
printf("V[5]=%d\n",V[5]);
printf("V[6]=%d\n\n",V[3]);
printf("Optimalniy puty\n\n"); G[1]=E[2]+E[7]; G[2]=E[1]+E[5]+E[7];
G[3]=E[0]+E[3]+E[5]+E[7]; G[4]=E[1]+E[6]+E[8];
G[5]=E[0]+E[3]+E[6]+E[8]; G[6]=E[0]+E[4]+E[8]; if((G[1]<G[2])&&(G[1]<G[3])&&(G[1]<G[4])&&(G[1]<G[5])&&(G[1]<G[6])){
printf("V[1]->V[6]->V[5]\n\n");} else
if((G[2]<G[1])&&(G[2]<G[3])&&(G[2]<G[4])&&(G[2]<G[5])&&(G[2]<G[6])){
printf("V[1]->V[3]->V[6]->V[5]\n\n");} else
if((G[3]<G[2])&&(G[3]<G[1])&&(G[3]<G[4])&&(G[3]<G[5])&&(G[3]<G[6])){
printf("V[1]->V[2]->V[3]->V[6]->V[5]\n\n");} else
if((G[4]<G[2])&&(G[4]<G[3])&&(G[4]<G[1])&&(G[4]<G[5])&&(G[4]<G[6])){
printf("V[1]->V[3]->V[4]->V[5]\n\n");} else
if((G[5]<G[2])&&(G[5]<G[3])&&(G[5]<G[4])&&(G[5]<G[1])&&(G[5]<G[6])){
printf("V[1]->V[2]->V[3]->V[4]->V[5]\n\n");} else
if((G[6]<G[2])&&(G[6]<G[3])&&(G[6]<G[4])&&(G[6]<G[5])&&(G[6]<G[1])){
printf("V[1]->V[2]->V[4]->V[5]\n\n");} printf("Nagmite ENTER
dlya vihoda"); getchar(); getchar(); } |
//Масив усіх можливих
шляхів// //Масив вершин графа// //Масив ребер(дуг) графа// //Заповнення масиву
ребер(дуг) графа// // Присвоєння першій вершині
нульового знчення // //Присвоення всім іншим
вершинам нескінченності// //Знаходження короткої
відстані до вершини "2"// //Знаходження короткої
відстані до вершини "3"// //Знаходження короткої
відстані до вершини "4" та "5"// //Знаходження короткої
відстані до вершини "6"// // Відстані усіх можливих шляхув // // Вивод на екран однієї найкоротшої відстані з вище перелічених // |