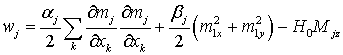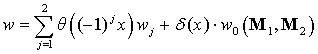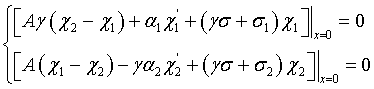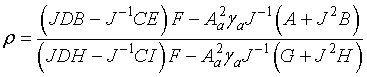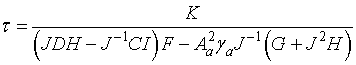Физика/ 1. Теоретическая физика

Doctor of Phys. and Math. Sci. Reshetnyak S.O.

National Technical University of Ukraine «Kyiv Polytechnic Institute»

Reflecting properties of ferromagnetic spin lens with non-ideal boundaries

In the present paper a spin-wave lens is proposed to be constructed on the base of three-layer ferromagnetic material with layers located perpendicularly to x axis. The first and third (along the x axis) parts are semi-infinite homogeneous uniaxial ferromagnets with corresponding parameters of exchange interaction , , uniaxial magnetic anisotropy , , saturation magnetization ,, and between them a uniform layer is located having thickness a and magnetic parameters , , . Easy axis is parallel to the direction of external permanent uniform magnetic field and z axis.

The energy density of such magnetic structure in exchange mode and taking into account the condition looks like

(1)

where M_j = M_0je_z+m_j, m_j are unit vectors describing deviations of magnetization vector from equilibrium state. Equilibrium state of magnetic moment is along z axes.

Boundary conditions. Boundary conditions are proposed for the case of non-ideal interfaces. Suppose, two uniform unbounded ferromagnets contact along yz plane and the system’s energy density can be written as

,

where is Heaviside function, is delta function,

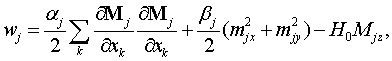
and

.

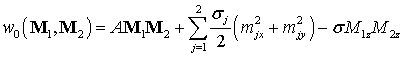A boundary is characterized with a coupling parameter A of interaction between two parts of system, parameters of inhomogeneous magnetic anisotropy of the parts in an interface, , and a parameters of inhomogeneous magnetic anisotropy caused by interaction of lattices of two subsystems in an interface.

Integration of a corresponding equation of magnetization dynamics on a small area in a vicinity of a boundary with subsequent convergence to zero of area’s square results in the following boundary conditions:

.

(1)

where .

Spin wave reflection. Taking into account that we use a model of thin lens, we approximate the distribution of magnetic parameters by the way shown in fig.1 to calculate reflection characteristics of our inhomogeneity that we named “lens”. Obviously, this object carries out the function of lens if only gives a good transmission of spin waves, and we obtain a mirror if not. Therefore, we need estimate a reflecting ability of an inhomogeneity.

Figure 1. The model of the structure to estimate its reflecting ability.

Using boundary conditions (1) for both boundaries, we obtain:

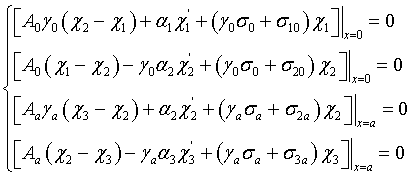(2)

Let’s associate in (2) the following expressions to incident, reflected and transmitted waves:

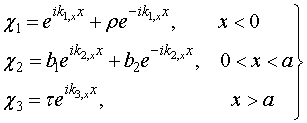(3)

Here ρ is a complex reflection amplitude of a spin wave, τ is a transmission amplitude. Then, taking into account (2), (3), we obtain (parameters in the next expression characterize functional dependencies):

.	(4)
.	(5)

Fig. 2 shows field and frequency dependencies of reflection coefficient.

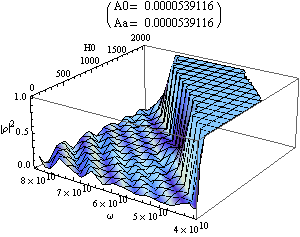
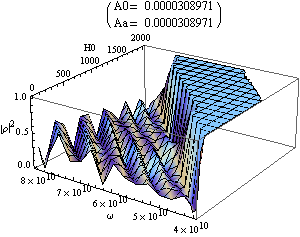Figure 2. Dependence of reflection coefficient on frequency and magnetic field at different values of coupling parameters A₀=A_a.