УДК 681.5.015

 

АВТОМАТИЗАЦІЯ ТЕХНОЛОГІЧНОГО ПРОЦЕСУ ПЕРЕКАЧУВАННЯ ПРИРОДНОГО ГАЗУ НА ЗАСАДАХ МЕТОДІВ ФАЗЗІ-ЛОГІКИ

 

В.С. Борин, О.В. Єфремов, О.В.Олескин

Івано – Франківський національний технічний університет нафти і газу,

76019, Івано-Франківськ, Карпатська, 15, тел.(03422)48003, е-mаil:kafatp@ukr.net

 

Досліджено систему оптимального управління при навантаженні між ГПА компресорного цеху. Елементами рівня цієї системи є технологічні процеси з діючими на них автоматизованими системами управління, а центром – плануючий орган роботи ГПА. В моделі елементів, які можуть мати дуже складну структуру і велику розмірність, входять технологічні керуючі впливи, температура, тиск, вібрація, тощо. Нас цікавлять загальні показники, в частці перекачування газу та оптимальна робота ГПА. Зрозуміло, що при будь-якому розумному критерії центра оптимальним режимом технологічного процесу може бути тільки такий режим, порівняно з яким не можна одночасно збільшити ККД роботи ГПА та знизити витрати на його роботу та обслуговування.
      Розглядаємо вектор   який належить множині Парето та множині ефективних точок задачі векторної оптимізації:

                                                   (1.1)

Вектор   в якості координуючого сигналу, центр якого відповідає його елементам, а процедура координації буде складатися із почергового розв’язку локальних задач оптимізації і координуючої задачі роботи ГПА.

При розв’язку даної задачі локальної оптимізації ГПА виконано відображення:

                                               (1.2)

де  і  – відповідно координуючий сигнал центру, що поступає до і-го елемента на t-му кроці ітераційної процедури і відповідає цьому сигналу вектор показників із множини Парето.

При розв’язку координуючої задачі оптимізації ГПА  виконано  відображення:

                                                      (1.3)

де  – множина ефективних векторів F, отриманих центром від елементів до t-го кроку.

Конструктивні алгоритми розв’язку задач (1.2) і (1.3) при умові, що центр намагається максимізувати цільову функцію , частковим випадком при цьому виступає відома задача розподілу ресурсів, яка набула вигляду:

                                                  (1.4)

                                            (1.5)

                            (1.6)

Розглянуто алгоритм розв’язку нашої задачі в ситуації, коли модель центра є нечіткою з теорії Заде, а прийняті рішення здійснювалися експертом в ході процедури людина-машина. При цьому отримали значення із задачі (1.4) - (1.6).

Сконкретизували вид нечіткості. Умова (1.5) формуються експертом словесно, наприклад : «Допустимо, щоб  було не менше ніж С1 і бажано, щоб не менше, ніж С2».

Цій фразі поставлено у відповідність нечітку множину. Найбільш простий спосіб задання функції належності цієї множини знаходимо за наступною формулою:

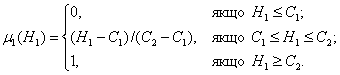                           (1.7)

Відповідно побудували нечітку множину , яка є цільовою функцією . Максимізували нашу функцію належності, яка знаходиться через функцію відповідності   і вектор терезів , де  вказує степінь важливості k-го критерію  або відповідно цьому критерію функції :

                                  (1.8)

Із (1.7) і (1.8) бачимо, що в k-ий критерій центру  входить k-і показники елементів , тому  задає навіть відносну важність показників елементів і є координуючим сигналом, центр якого посилює елементи.

Функції  мають такі форми:

                                   (1.9)

                          (1.10)

Вагові коефіцієнти  знайшли шляхом обробки відповідей експерта на задані йому запитання. Успіх процедури людина-машина в багато чому залежить від того, чи будуть ці запитання достатньо природними для експерта. На наш погляд, цій умові задовольняє процедура, в якій експерту представляють для порівняння два можливих варіанта і просять їх якісно порівняти, використовуючи заданий набір термів. Звідси введемо набір: «еквівалентно», «дещо краще (гірше)», «набагато краще (гірше)», «строго краще (гірше)».

Ці слова являються лінгвістичними мітками нечітких множин, згаданих на базовій множині

,                                   (1.11)

де ,  – допустимі.

Так як , то

Функції належності терма «еквівалентно» і «набагато краще» задаємо формулами відповідно

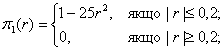                                       (1.12)

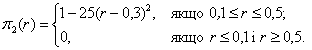                                (1.13)

При порівнянні варіантів  і  експерт вибрав лінгвістичну мітку  [функція відповідності відповідної нечіткої множини ]. Тим самим задаємо нечітку множину якій належить вектор .

Функція відповідності цієї множини

                                                 (1.14)

де                                                

Якщо проводиться L порівнянь, то отримаємо функції належності. Результуючу функцію відповідності знаходимо як перетин функцій:

                                                 (1.15)

Вектор, який має максимальне значення функції належності,

                                                 (1.16)

Цей вектор і є координуючим сигналом, який посилає елементам центр.

     В подальшому ми перейшли до системи наближеної рівності та розглянули нашу задачу як :

                       (1.17)

В свою чергу чітка модель при автоматизації ГПА має вигляд:

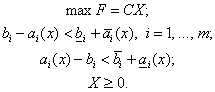                                    (1.18)

ГПА включає багатокритерійне завдання та набуває наступного вигляду:

                    (1.19)

 Де функція належності:

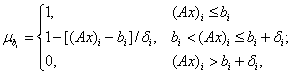                                   (1.20)

       Тоді завдання вирішили стандартними прийомами:

                                                                                               (1.21)

Для нашого завдання використали наступну модель:

                                                 (1.22)

Довели, що існує вектор  такий, що розв’язок задачі

                                   (1.23)

є в той же час розв’язком поставленої задачі. Тут  – міцність множини X.

Приводимо також модель наближеного розподілу ресурсів і багатокритерійну неопуклу модель виробничої програми. Для вирішення останнього використали алгоритм Falk – Soland, який при використанні методу гілок і меж дозволив отримати послідовність допустимих крапок, що є вирішенням ряду необхідних нам підзадач.

Розв’язано задачу планування в нечіткому середовищі, засновану на LR-представленні нечітких множин, але що відрізняється від описаних в літературі.

Ввели наступні визначення.

Нечітке число  менше нечіткого числа  (рис. 1.2), якщо

                                     (1.24)

Нечітке число  більше нечіткого числа , якщо

.                          (1.25)

Рис

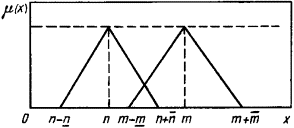
Рисунок 1.2 – Функція приналежності нечіткого числа

 

Нечітке число  рівне нечіткому числу , якщо

              .             (1.26)

На підставі визначень (1.24) – (1.26) перейшли до чіткого аналога системи (5.3):

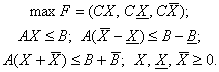                                      (1.27)

Агрегуючи змінні:

                                                   (1.28)

декомпозуємо (1.27) на наступні системи:

                                               (1.29)

                  (1.30)

    .                  (1.31)

У системи (1.30) і (1.31) введені додаткові обмеження, що відображають той факт, що повинна виконуватися нерівність:

                                           (1.32)

де х* – оптимальне вирішення нашої системи (1.29).

Вирішивши системи (1.29) – (1.31), визначили значення х*, х’*, х"*.

Тоді нечітке рішення нашої задачі в RL-зображенні (рис. 1.3) запишемо як

  .                              (1.33)

Рис

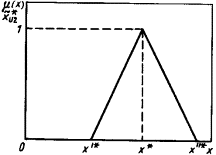
Рисунок 1.3 – Нечітке рішення задачі оптимізації при RL-представленні

Якщо нижнє і верхнє відхилення вектора  пропорційні середньому значенню, то справедлива теорема: якщо для нечіткого числа  виконується умова:

                                   (1.34)

і система (1.29) має рішення х*, тоді (1.30) і (1.31) мають рішення:

.                                  (1.35)

Доводимо: Нехай (1.29) має рішення х*. Розіб’ємо матрицю А на дві підматриці (за умови ): Б – квадратну  і N – розмірністю :

.                                               (1.36)

Розіб’ємо змінні і вектор цін відповідно:

                                            (1.37)

Тоді запишемо:

.                                                 (1.38)

     Звідки:

.                                             (1.39)

Значення функціонала

.                          (1.40)

Як відомо, умова допустимості має вигляд

.                             (1.41)

Враховуючи, що в оптимальному розв’язку небазисні змінні рівні нулю, умова (1.41) буде мати вигляд

.                                              (1.42)

Умову оптимальності запишемо як

.                                          (1.43)

Як видно з (1.42), (1.43), зміна правої частини приведе до зміни лише умови допустимості (1.41).

Запишемо в аналогічному вигляді розв’язок задачі (1.29):

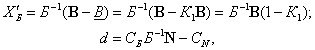                         (1.44)

але  Так як  – допустиме рішення (1.29) і  то  Звідси випливає, що:

Думаючи аналогічно, отримаємо:

                                               (1.45)

що і потрібно було доказати в результаті чого для отримання кінцевого результату тобто, отримання нечіткого розв’язку системи  нас задовольняє  розв’язок системи (1.29), яка в свою чергу є розв’язком систем (1.30) і (1.31) і  розраховується за формулою (1.33).

         Висновком розв’язку даної задачі є те, що вперше застосовано оптимізаційний метод який використовує фаззі-логіку при пошуку оптимальних рішень для розв’язку задачі розподілу навантаження між ГПА компресорного цеху з використанням моделі енергетичного балансу та контролю допустимих меж різності навантаження ГПА. Подальший розвиток моделі і методу оптимізації передбачається виконати для послідовно-рівнобіжної схеми роботи ГПА і розподілу навантаження між агрегатами різної потужності об'єднаних гідравлічним режимом.

Список літературних джерел

1.                      Беллман Р., Заде Л. Принятие решений в расплывчатых условиях. В кн.: Вопросы анализа и процедуры принятия решений. - М.: Мир, 1976. - С. 172-215.

2.                      Заде Л. Понятие лингвистической переменной и ее применение к принятию приближенных решений. - М.: Мир, 1976. - 167 с.

3.                      Митюшкин Ю.И., Мокин Б.И., Ротштейн А.П. Soft-Computing: идентификация закономерностей нечеткими базами знаний. - Винница: УНІВЕРСУМ-Вінниця, 2002. -145 с.

4.                      Ротштейн А.П. Интеллектуальные технологии идентификации: нечеткая логика, генетические алгоритмы, нейронные сети. - Винница: УНІВЕРСУМ-Вінниця, 1999. - 320 с.

5.                      Ротштейн А.П., Штовба С.Д. Проектирование нечетких баз знаний: лабора­торный практикум и курсовое проектирование: Учебное пособие. - Винница: Винницкий государственный технический университет, 1999. - 65 с. (На укр. языке).