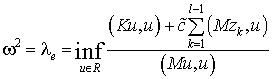Trubachev S.I., Kolodezhnyj V.A.

National technical University of Ukraine “Kiev Polytechnic Institute”

THE VIBRATIONS OF MECHANICAL SYSTEMS WITH ENERGY DISSIPATION

The accounting of energy dissipation in mechanical systems, which based on the hypothesis of Boca-Schlippe-Kolar, was conducted mainly for systems with 1–2 degrees of freedom [2, 3]. This is explained by the fact that the solutions of problems of the system’s oscillations are investigated by analytical methods with a small number of degrees of freedom. It should be emphasized that the study of mechanical systems’ dynamic based on a discrete-continuum models, which are formed on the basis of the variational-grid approach and suggests a spreading of the hypothesis of Boca-Schlippe-Kolar on a system with many degrees of freedom.

The problem of forced oscillations of a system with N degrees of freedom will be considered in the framework of the theory which based on the hypothesis of Boca-Schlippe-Kolar.

The differential equation of the oscillatory system with one degree of freedom, taking into account the frequency-independent energy dissipation is given by [1]:

,

(1)

where are the coefficients of inertia, stiffness and frequency-independent friction; is the correction factor; is the own circular frequency; is an arbitrary exciting force.

The equation (1) is differ from the analogous equation in which the friction is taken into account by the Kelvin-Voigt hypothesis only in the presence of the correction factor .

Therefore, the hypothesis of Boca-Schlippe-Kolar is called "corrected" for the hypothesis of the Kelvin-Voigt. According to the hypothesis of Boca-Schlippe- Kolarthe friction is independent from frequency, which is typical for metallic structures. When using the hypothesis of Kelvin-Voigt, it’s assumed that the friction depends from the frequency, and this hypothesis is a good description for vibrations of structures which made out of polymeric materials.

In solving the problems of oscillations of numerical methods in the process of sampling designs turn to systems with N degrees of freedom.

The set of equations of oscillations of a system with many degrees of freedom can be represented by matrix equations:

,

(2)

in which , , are the matrices of inertia, stiffness and damping; is the matrix correction factors; , are the column vectors of arbitrary generalized coordinates and generalized random forces.

The form of the matrix is generally not known and its presence is a major challenge for solving the matrix equation (2).

The friction that occurs in the system, we’re considering the internal, which is caused by material’s imperfect elasticity. Then, we can be assumed that the friction coefficient is a small part of the stiffness:

,

(3)

where is the coefficient of not-in-phase deviations from Hooke's law.

We generalize the relation (3) in the event of a system with N degrees of freedom, considering the coefficient by the characteristic of the material:

.

(4)

Let’s present a system of equations (2) in the diagonal form with using a linear transformation:

,

(5)

where , are the columns of vectors of an arbitrary and major generalized coordinates; is the matrix of amplitude coefficients of the characteristic vibrations of the system with N degrees of freedom. Each column of this matrix defines its own proper irregular form of the oscillations, in generally.

Natural vibration modes are satisfied the orthogonality conditions and formulas for the reduction of kinetic and potential energy:

, ,

(6)

where and are the diagonal matrix of the main coefficients of inertia and the main stiffness coefficients.

From (5), (6) we can be obtained:

,	(7)
, .	(8)

To find the normalized vibration modes with unit norms on the kinetic energy it’s necessary to divide the elements of each column in non-symmetric matrix on the appropriate energy norm.

We obtain

, ,

(9)

where is the normalized vibration modes. Substituting (4), (5) in (2) and multiplying the result by on the left, taking into account the expression (6), we obtain a system of equations in the main generalized coordinates:

(10)

For the full separation of the variables is need to be taken

(11)

The expression (11) for the matrix of correction factors is the most common. It allows us automatically to take into account the frequency-independent friction in complex structures, which with the help of the discretization into finite elements are modeled by the matrix equations of the form (2).

It should be emphasized, that the using of (11) without the assuming (4), the complete separation of variables will not allow.

Thus, to solve the problem of oscillations of a system with N degrees of freedom, in view of frequency-independent energy dissipation, it’s necessary to determine the spectrum of natural frequencies and vibration modes. If you use numerical methods the infinite-dimensional space of admissible functions is replaced by finite through the discretization of system. The generalized eigenvalues problem is replaced by an approximation

.

(12)

To find the spectrum of natural frequencies and vibration modes we proposed to use the method of increasing stiffness [3], which is based on the minimization of functional of the Rayleigh-type:

.

(13)

Here is the earlier found the eigenmodes; is the coefficient, which is certainly higher than the desired eigenvalue. , are the matrix of stiffness and mass of the system.

The expression (13) shows, that the using of a method of increasing the rigidity does not require the formation of the vector orthogonal to previously found eigenvectors, which saves the computational resource.

Conclusions

In this paper we present the matrix equation taking into account energy dissipation in order to describe the process of forced oscillations for systems with N degrees of freedom that allows this approach to study the dynamics of plate-shell structures of aircraft. We obtain the matrix equations describing the energy dissipation in mechanical systems with N degrees of freedom and based on the hypothesis of Boca-Schlippe-Kolar.

To determine the spectrum of natural frequencies and vibration modes, which are used in the matrix equation, the method of stiffness is used in the work. It is more efficient and economical in terms of computational cost compared with traditional approach, where each last form and frequency determined by minimizing the Rayleigh-type functional on the subspace, which is orthogonal to the previously obtained eigenvectors. This makes it possible to solve the problems of a large dimension with limited memory resources of a PC.

References

1. Василенко Н.В. Теорія коливань і стійкості руху [Текст] / Н. В. Василенко, О. М. Алексейчук // – К.: Вища шк., 2004. – 525 с.

2. Бидерман В. Л. Теория механических колебаний [Текст] / В.Л. Бидерман // – М.: Высш. шк., 1980. – 408 с.

3. Бабенко А. Е. Определение частотного спектра и собственных форм колебаний упругих систем методом повышения жесткостей [Текст] / А. Е. Бабенко, О. А. Боронко, О. Н. Василенко, С. И. Трубачев // Проблемы прочности. – 1990, №2. – С. 122–124.