УДК 621.992.7

Бецко Ю. М., ст. викл., Коростильов В. Ю., студ.

Національний технічний університет України «Київський політехнічний інститут», м. Київ

ЗМЕНШЕННЯ НЕСТАЦІОНАРНОСТІ ПЕРИФЕРІЙНОГО ФРЕЗЕРУВАННЯ

На сьогодні фрезерування є найпродуктивнішим методом лезового оброблення металів, а тому і одним з найпоширеніших при обробленні деталей машин. Фреза – багатолезовий інструмент, застосовуваний для оброблення площин, пазів, тіл обертання, фасонних поверхонь і розрізання заготовок. Високу продуктивність при цьому забезпечує одночасна участь в роботі декількох зубів. Існує дві кінематичні схеми фрезерування – торцеве фрезерування і периферійне, а також їх комбінація – комбіноване фрезерування. При периферійному та комбінованому фрезеруванні (рис. 1) якість поверхні формується зубцями фрези, що знаходяться на циліндричній поверхні, при цьому різальна кромка має велику довжину, яка дорівнює ширині фрезерування .

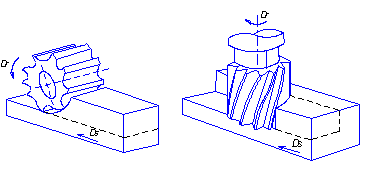
Рис. 1. Кінематичні схеми периферійного та комбінованого фрезерування.

Оскільки процес фрезерування є преривчастим, то різальні кромки вступають в роботу періодично і контактують з поверхнею різання на ділянці кута контакту , але і при цьому зуб працює з змінною товщиною зрізуваного шару, який для миттєвого значення кута контакту визначається

(1)

З зазначеного видно, що процес фрезерування характеризується непостійністю сумарних силових характеристик – окружної сили, крутного моменту, поздовжніх та поперечних сил. Це збурення призводить до появи вібрацій, що негативно впливає на якість обробленої поверхні, стійкість інструменту, роботу приводу верстата. Для більш плавної роботи абсолютна більшість фрез випускають зі спіральним розташуванням зуба, який має кут підйому гвинтової лінії . Але і це не дозволяє забезпечити великого значення рівномірності виникаючих сил.

Рис. 2. Сучасні конструкції фрез з гвинтовим зубом для периферійного та комбінованого фрезерування.

Розглянемо можливість вдосконалення процесу фрезерування, підбираючи оптимальну ширину фрезерування . Крок зубів по торцю фрези визначається:

(2)

Осьовий крок зубців фрези:

(3)

Для фрези з гвинтовим зубом кут повороту зуба буде різним для кожної точки різальної кромки (рис. 3) тому можна вести річ про кут повороту та товщину зрізуваного шару тільки для певної точки C.

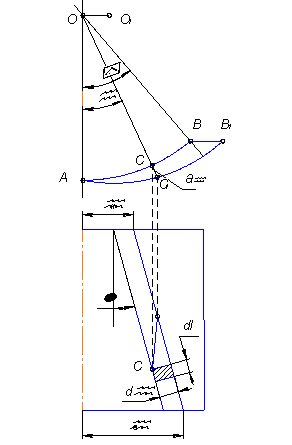
Рис. 3. Визначення перерізу зрізуваного шару фрези з гвинтовим зубом

Розглянемо елемент ширини зрізу в точці C при куті . Площа перерізу буде визначатися:

(4)

(5)

Тоді:

(6)

Сумуючи ці площинки по всій ширині зрізу в межах від (нижня границя кута) до (верхня границя кута) отримуємо:

(7)

або

(8)

Для визначення умови рівномірності спробуємо скласти величини зрізуваних шарів для всіх зубів, що знаходяться в зоні різання. Таким чином, для зубів, які врізаються, загальною кількістю маємо і тоді:

, (9)

для зубів з повним різанням кількістю – =1, і

, (10)

для зубів, що виходять з зони різання в кількості :

(11)

Якщо ширина фрезерування буде кратна осьовому кроку, то отримуємо:

(12)

тому

(13)

або

(14)

Отже маємо значення сумарної товщини зрізуваного шару по всім працюючим зубам фрези:

(15)

а, оскільки при глибині різання :

(16)

то

(17)

Тепер можна стверджувати, що умова рівномірності фрезерування виглядає так:

(18)

Це можна проілюструвати графіком на рис 4.

Таким чином, при виконанні даної умови, кожний зуб, що виходить з зони різання, дає стружку, переріз зрізу якої в сумі з перерізом зрізу зуба, що входить, має постійну величину. Ця величина дорівнює максимальному перерізу, який є на зубі, що повністю знаходиться в зоні контакту з заготовкою. Це означає, що теоретично, величини окружної сили, крутного моменту і потужності повинні залишатися постійними.

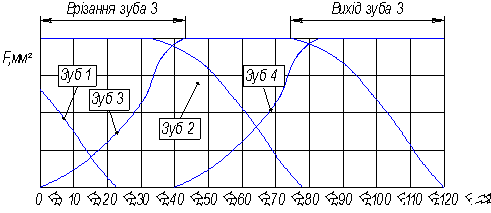
Рис. 4. Графік зміни миттєвої величини перерізу зрізуваного шару гвинтовими зубами фрези при периферійному фрезеруванні.

Використавши вищезазначені висновки було розроблено прикладну програму, за допомогою якої можна розрахувати оптимальну ширину фрезерування та сумарну площу зрізуваного шару (рис. 5).

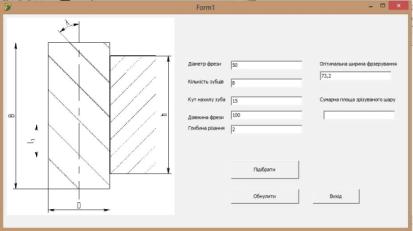
Рис. 5. Інтерфейс прикладної програми.

Література:

1. Рудник С. С. Основи теории фрезерования. Часть 1. Силовые зависимости при фрезеровании. Конспект лекций // Киев КПІ. – 1962. – 80 с.:іл.

2. Мазур М. П. Основи теорії різання матеріалів: підручник. – Львів: Новий світ–2000, 2010. – 422 с.

3. Ящерицын П.И. Теория резания: учеб./ П.И. Ящерицын, Е.Э. Фельдштейн, М.А. Корниевич.- Мн.: Новое знание, 2005.-512с.