К.т.н. Твердоступ Н.И.

Днепропетровский национальный университет им. Олеся Гончара

ИЗМЕРИТЕЛЬНЫЙ ГЕНЕРАТОР НА ОСНОВЕ

КОМБИНИРОВАННОЙ ОПЕРАЦИОННОЙ СХЕМЫ

 

В устройствах измерения и контроля широко используют метод F-метра, позволяющий преобразовывать реактанс датчика в частоту гармонических колебаний [1]. Недостатком метода является его ограниченная чувствительность к изменению контролируемого параметра.

Целью работы является разработка F-метра с повышенной чувствительностью к изменению индуктивности параметрического датчика.

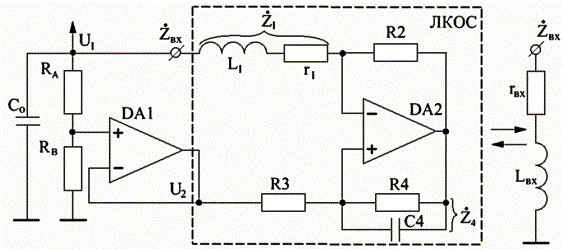
Измерительный генератор (рис. 1) на основе линейной комбинированной операционной схемы (ЛКОС) в цепи отрицательной обратной связи усилителя DA2 содержит индуктивный датчик. Из [2] следует, что входной импеданс ЛКОС равен

 = (                                    (1)                                            

где – комплексный импеданс индуктивности L1 с активным

 

                                               а)                                                   б)

Рис. 1 – Измерительный генератор на основе ЛКОС (а);

эквивалентное представление ЛКОС (б)

сопротивлением r1;  R2, R3  – сопротивления цепи комбинированной обратной связи усилителя DA2;  – импеданс параллельно соединенных сопротивления   и емкости ; n = U2 / U1, U1 и U2 –напряжения сигналов возбуждения. Повторитель на усилителе DA1 с делителем RА, RВ представляет собой источник напряжения возбуждения U2 , синфазного напряжению U1. Отношение n напряжений возбуждения можно представить  в виде

                                              (2)

тогда входной импеданс , выраженный через параметры схемы, будет                             

                   (3)

 = rвх + Lвх ,                                                      (4)

где rвх, Lвх – входные активное сопротивление и индуктивность. Из (3) и (4) следуют выражения активной и индуктивной составляющих входного импеданса

                                 (5)

                                  (6)                               

показывающие, что в настоящей схеме L1 и r1 преобразуются в Lвх и rвх с коэффициентом умножения равным  Из (5) также следует, что со-                                                                                         

противление r1 компенсируется отрицательной активной составляющей входного импеданса ЛКОС равной

.                                            (7)

Из (6) видно, что умножение индуктивности L1 на коэффициент m происходит одновременно с уменьшением ее начального значения на величину , которую будем называть компенсирующей индуктивностью Lк. Выражение (6) представим в виде

 .                                               (8)

Допустим, что под воздействием контролируемого параметра индуктивность L1 изменяется на величину ΔL1, тогда входная индуктивность ЛКОС становится

 .                            (9)

Из (8), (9) следует, что абсолютное и относительное приращения входной индуктивности равны

                                                   (10)

                                        (11)

причем, при Из (10), (11) следует, что в ЛКОС возможно масштабирование индуктивности датчика с управлением величины чувствительности к контролируемому параметру.

К входу ЛКОС подключена емкость, которая с входной индуктивностью   образует колебательный контур с резонансной частотой

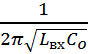  .                                                  (12)

Из (5 ) следует, что при выполнении условия

r1< 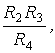                                                       (13)

в контуре присутствует отрицательное активное сопротивление, обеспечивающее стационарные гармонические колебания на резонансной частоте (12), которая с учетом (8) имеет вид

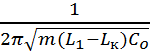  .                                         (14)

При изменении индуктивности датчика  приращение частоты можно определить в виде

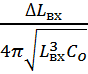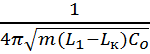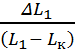   =     =    · .   (15)

Из (15) видно, что приращение частоты существенно увеличивается при   Именно это указывает на возможность повышения чувствительности F-метра на основе ЛКОС к изменению индуктивности L1 параметрического датчика.

        Экспериментальная проверка выражения (15) была проведена на измерительном генераторе (рис.1), собранном на операционных усилителях ICL7650 с индуктивностью L1 = 21 мГн, емкостью  = 1,106 мкФ и начальной частотой колебаний 460 Гц. Результаты эксперимента (рис. 2) показывают, что зависимости  линейны; без компенсирующей индуктивности    (зависимость 5)

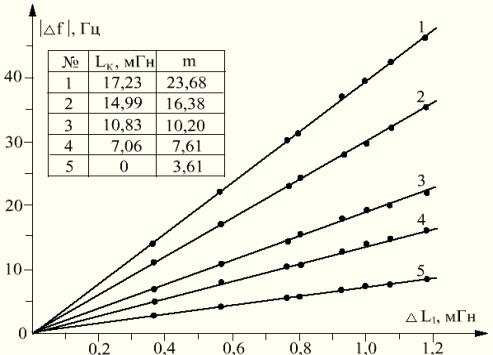
Рис. 2 – Приращение частоты  генератора как функция индуктивности        датчика  L1 для разных значений компенсирующей индуктивности Lк

 

чувствительность к  минимальная и составляет 7,5 Гц/мГн, при индуктивности   17,23 мГн (зависимость 1) чувствительность возрастает в пять раз до 39,2 Гц/мГн. Отличие экспериментальных и расчетных по (15) данных не превышает 5%.

         Вывод. Компенсация начальной индуктивности датчика с умножением ее приращения позволяют увеличить приращение частоты измерительного генератора на основе линейной комбинированной операционной схемы.

 

         Литература:

1.   Измерения в электронике: Справочник / В.А. Кузнецов, В.А. Долгов, В.М. Коневских и др.; Под ред. В.А. Кузнецова. – М.: Энергоатомиздат, 1987. – 512 с.

2.     Твердоступ Н.И. Обобщенная модель преобразователей импеданса // Вісник Дніпропетр. ун-ту. Фізика. Радіоелектроніка. – 2010. – Вип. 17, №2. – С. 103 - 108.