Экономические науки/8 математические методы в экономике

Дмитренко И. С. , к.ф-м.н.Колесников С. А.

Донбасская государственная машиностроительная академия, Украина

Кафедра высшей математики

Многоцелевое программирование в курсе исследования операций.

Применение экономико-математических моделей в учебном процессе является актуальным при изучении дисциплин экономического профиля. Отметим, что постановка экономической проблемы должна быть интересна студенческой аудитории. В то же время, ее реализация в виде математической модели должна иметь достаточно простое решение, и понятную экономическую интерпретацию. Подбор экономико-математических моделей является кропотливым делом, которому преподаватель должен уделять постоянное внимание. Отметим, что в последнее время значительно увеличилось количество литературы, помогающей в подготовке к занятиям, что позволяет совершенствоваться преподавателю. Современное производство и сфера обслуживания требует подготовки специалистов нового уровня и новых специальностей. Поэтому агрегированные науки являются настоящим подспорьем специалистам будущих специальностей. Развивать и совершенствовать аппарат математических моделей при изучении дисциплины исследование операций является одной из основных задач математики высшей школы.

В нашей работе пойдет речь о некоторых математических аспектах молодого и интересного направления исследования операций – многоцелевого программирования. Данное направление более естественно считать обобщением линейного программирования, где линейная целевая функция всего одна для простоты проблемы. На самом деле, экономисту важно найти решение проблемы не просто для того, чтобы максимизировать прибыль предприятия. К другим требованиям, например, относятся минимизация расходов всех видов материала и окончательной себестоимости продукции. Это ведет к увеличению количества целевых функций. При постановке задачи такие функции в совокупности часто бывают противоречивыми по своей сути, и тогда приходится находить компромиссное решение. Постановка и изучение экономико-математических моделей со многими целевыми функциями является актуальным для современного производства. Мы считаем, что специалисты, обладающие подобными знаниями и навыками, будут иметь большую уверенность на рынке труда, поэтому ввели в курс классического исследования операций раздел многоцелевое программирование. Не смотря на своевременность и важность изучения экономико-математических моделей со многими целевыми функциями, данной проблеме в учебной литературе уделяется недостаточное внимание. Трудоемкость решения конкретных задач заставляет подбирать и находить только те модели, которые могут быть внедрены в учебный процесс.

Среди известных методов решения отметим следующие:

· Метод последовательных уступок;

· Построение единого показателя эффективности посредством суммирования произведений имеющихся показателей на «весовые» коэффициенты (коэффициенты важности показателей);

· Превращение всех целевых функций, кроме одной, в ограничения;

· Метод идеальной точки.

Нами разработан набор экономико-математических моделей для курса исследования операций со следующей постановкой задачи: две целевые функции зависят от двух переменных, ограничения являются линейными. Для их решения применяется метод идеальной точки, использующий геометрическую интерпретацию и понятие о множестве Парето. В период преподавания курса исследования операций было отмечено, что наиболее наглядными и запоминающимися методами являются именно геометрические методы.

Далее рассмотрим экономическую проблему, иллюстрирующую данный метод.

Фирма выпускает два вида изделий по цене 2 ден.ед. и 3 ден.ед. соответственно. По результатам маркетинговых исследований спрос на изделия обоих видов не менее 5 тыс.ед. в год. Для производства изделий используются материалы вида А и В, запасы которых на фирме составляют 4 и 13 т соответственно. Для изготовления 1 тыс. изделий норма расхода материала А не используется, а для изделий 2-го вида-1т. Для изготовления 1 тыс. изделий материала В расходуется: для изделий 1-го вида – 3т, для изделий 2-го вида – 1т. Себестоимость изделий 1-го вида – 1 ден.ед., а 2-го вида – 2 ден.ед.

Найти оптимальное решение по производству изделий 1-го и 2-го видов, чтобы прибыль была максимальной, а себестоимость минимальной.

Обозначим x – количество изделий 1-го вида, тыс.ед.; y – количество изделий 2-го вида, тыс.ед.

Математическая модель задачи будет иметь вид: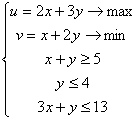

Выполним замену , тогда задача примет вид:

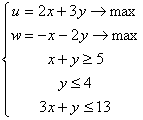
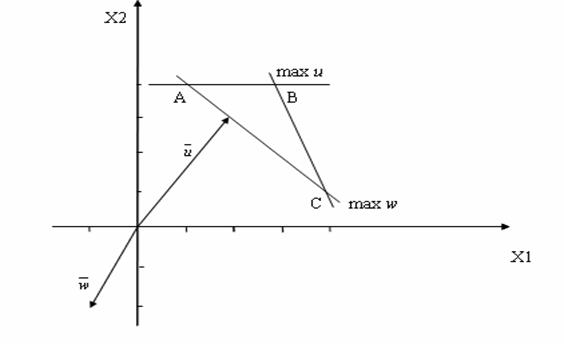
Построим множество решений на плоскости . В данном примере это множество представляет собой треугольник АВС, вершины которого имеют координаты: А(1,4), В(3,4), С(4,1).

Так как критерии являются линейными, то треугольник АВС переходит в треугольник А₁ В₁ С₁ , координаты вершин которого можно вычислить с помощью преобразования .Построим треугольник А₁ В₁ С₁, координаты вершин которого: А₁(14,-9), В₁(18,-11), С₁(11,-6).

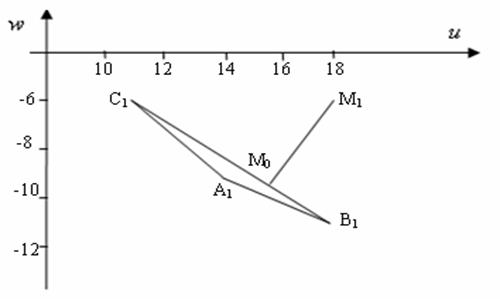
Найдем границу Парето полученного отображением множества. Это отрезок С₁ В₁. Точка утопии М₁ (18,-6) ,ее координаты- это наибольшие значения функций на множестве решений . Требуется найти на множестве Парето точку, ближайшую к точке М₁. Данная задача является типичной задачей аналитической геометрии и ее решение не представляет большого труда. Итак, ближайшая к точке М₁ на границе Парето - точка М₀(15,63;-9,31). Найдем координаты полученной идеальной точки М на множестве плоскости путем решения соответствующей системы:

.

В итоге получим: М₀(15,63;-9,31)- идеальная точка, а М(3,34;2,99)- решение поставленной задачи.

Итак, фирме необходимо выпускать 3,34 тыс.ед. изделий 1-го вида и 2,99 тыс.ед. изделий 2-го вида. При этом, максимальная прибыль составит 15,63 ден.ед., а минимальная себестоимость – 9,31 ден.ед.

Литература:

1. Красс М.С. Основы математики и ее приложения в экономическом образовании: Учебник-М.: Дело,2002.-459-365с.

2. Таха, Хэмди А. Введение в исследование операций.-М.:Изд.дом «Вильямс», 2001.354-369с.

3. Трояновский В.М. Математическое моделирование в менеджменте. Учебное пособие. –М.:Издательство РДЛ.2002.107-110с.

4. Шикин Е.В., Чхартишвили А.Г. Математические методы и модели в управлении:Учеб.пособие.-М.:Дело,2002.158-170с.