Рыкова О.В.
Белорусский Государственный Аграрно-технический университет,
Беларусь
О гипотезе Спринджука для нормированных многочленов
третьей степени в декартовом произведении полей комплексных и поле р-адических чисел.
Рассматриваемая задача относится к
метрической теории диофантовых приближений зависимых величин.
Хотя мы постоянно работаем с
понятиями теории меры и теории вероятностей, они являются лишь удобной формой
для выражения получаемых теоретико-числовых закономерностей. С точки зрения
теории вероятностей все доказанные теоремы являются утверждениями типа «закона
нуля-единицы» с тем существенным дополнением, что мы всегда указываем, в каком
случае будет «нуль» и в каком «единица».
В 
в полях действительных
чисел, комплексных чисел и
р-адических чисел. В 
, где 
,
, 
, а 
простое число. эта
гипотеза была решена в
Мы доказываем гипотезу Спринджука в
поле 
для нормированных
многочленов.
Нормированными (или моническими) называются многочлены со старшим коэффициентом
1. Пусть 
– многочлен с целыми коэффициентами, 
– высота многочлена 
. Эти многочлены привлекают внимание тем, что их корни – целые алгебраические числа, а если в качестве
взять трансцендентное
число, то величина модуля 
(в архимедовой и
р-адической метрике) дает представление о близости числа к алгебраическому
целому. Такие результаты интересны не только в теории диофантовых приближений,
но и в приложениях (см.[1]). Пусть 
– фиксированное простое
число, 
– поле р-адических чисел с р-адической метрикой 
и мерой Хаара 
[2, c. 68-76, 84]. В
поле 
в качестве меры 
берем меру, равную
произведению меры Лебега 
в С и меры Хаара 
в , т.е. 
. Для нормированных многочленов доказана
Т е о р е м а 1. Для
любого 
неравенство
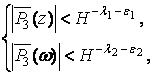(1)
в котором 
, имеет только конечное число решений в нормированных многочленах
для почти всех (в
смысле меры) точек 
.
Для доказательства
теоремы нам понадобятся следующие леммы, в которых 
будут обозначать положительные абсолютные постоянные.
Л е м м а 1. Пусть 
– многочлены с целыми коэффициентами, 
– их высоты 
, 
. Тогда
, где 
.
Доказательство см. в [2, с.26].
Пусть 
– корни фиксированного
многочлена в поле С, а 
– его корни в 
, где – наименьшее поле,
содержащее 
и все алгебраические
над числа. Положим
, 
.
Ясно, что, например, множеству 
принадлежат все комплексные числа z,
удаленные от 
не более чем
от других корней. Следующие леммы 2-6 относятся к многочленам, не имеющим
кратных корней.
Л е м м а 2. Если 
, то
.
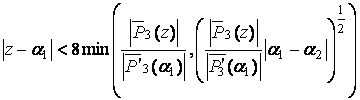Лемма доказывается аналогично лемме 2
[2, с.19], при 
.
Далее будем использовать дискриминант
многочлена , который обозначим через 
. По определению
(3)
и хотя бы один из коэффициентов 
равен 
.
Л е м м а 3. В условиях леммы 2 всегда
,
а если 
– комплексный корень, то верно также
.
Л е м м а 4. При 
и 
справедлива оценка
.
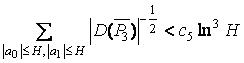Доказательство см. в [3, с.
114-115].
З а м е ч а н и е. Лемма остается справедливой и в двух других случаях,
когда 
или 
, а суммирование производится соответственно по оставшимся
коэффициентам , не превосходящим величину Н.
Л е м м а 5. Пусть 
и 
. Тогда
.
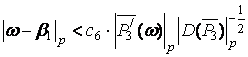Лемма доказывается
аналогично лемме 6 [2, с.87], при .
Л е м м а 6. Пусть 
и 
– произвольно малое число. Пусть 
обозначает количество
многочленов 
высоты Н, имеющих
дискриминант 
. Тогда
, где 
и 
– наибольшие целые числа,
квадраты которых входят множителями соответственно в Н и 
, а 
– свободный от
квадратов множитель числа 3.
Доказательство см. в [2, с.
140-141].
Л е м м а 7. (Бореля-Кантелли) Пусть (на прямой или плоскости) дана система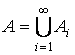 
измеримых множеств 
с условием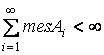 
. Тогда мера множества точек, попадающих в бесконечное число
множеств , равна нулю.
Работа выполнена в рамках
государственной программы фундаментальных исследований Беларуси «Математические
модели».
Литература
1. П т а ш н и к Б.И.
Некоторые задачи для дифференциальных уравнений с частными производными. Киев:
Навуковая думка. 1984.
2. С п р и н д ж у к В.Г. Проблема
Малера. Мн.: Наука и техника. 1967.
3. Ш а м у к о в а Н.В. // Вестнiк МДУ iмя А.А. Куляшова. сер.
Мат.,фiз, экалогiя, бiял. 2005, № 4 (22). С. 112-116.