Ленюк М.П.
Чернівецький факультет НТУ «ХПІ»
Підсумовування функціональних рядів за власними
елементами гібридного диференціального оператора Ейлера – (Конторовича -
Лєбєдєва) на полярній вісі ![]()
Розглянемо
задачу про конструкцію обмеженого на множині ![]() розв’язку сепаратної
системи звичайних диференціальних рівнянь Ейлера й Бесселя з виродженням при
старшій похідній
розв’язку сепаратної
системи звичайних диференціальних рівнянь Ейлера й Бесселя з виродженням при
старшій похідній
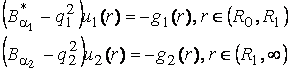 (1)
(1)
з крайовими умовами
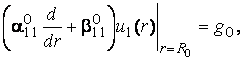
![]() (2)
(2)
та умовами спряження
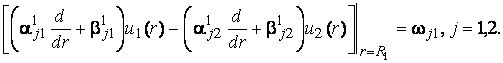 (3)
(3)
У системі (1)
беруть участь диференціальні оператори Ейлера 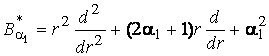 [1] та Бесселя
[1] та Бесселя 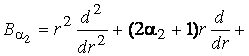
![]() [2], де
[2], де ![]()
![]() Вважаємо, що виконані
умови на коефіцієнти:
Вважаємо, що виконані
умови на коефіцієнти: ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Фундаментальну
систему розв’язків для диференціального рівняння Ейлера ![]() утворюють функції
утворюють функції ![]() та
та ![]() [1]; фундаментальну систему розв’язків для диференціального
рівняння Бесселя
[1]; фундаментальну систему розв’язків для диференціального
рівняння Бесселя ![]() утворюють модифіковані
функції Бесселя
утворюють модифіковані
функції Бесселя ![]() та
та ![]() [2].
[2].
Наявність
фундаментальної системи розв’язків дозволяє будувати розв’язок крайової задачі (1)- (3) методом функцій Коші
[1,3]:
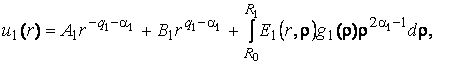
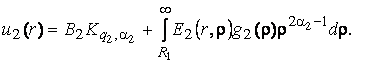 (4)
(4)
У рівностях
(4) беруть участь функції Коші [1,3]:
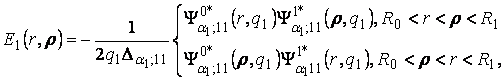 (5)
(5)
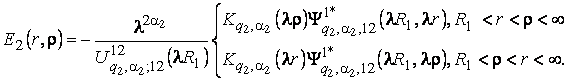 (6)
(6)
У рівностях
(5), (6) беруть участь функції:
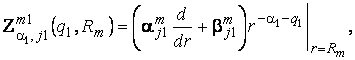
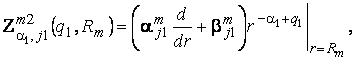
![]()
![]()
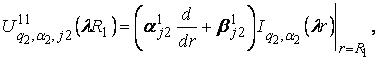
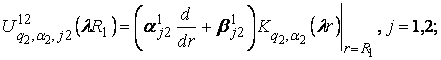
![]()
Крайова умова
в точці ![]() й умови спряження в
точці
й умови спряження в
точці ![]() для визначення величин
для визначення величин
![]() дають алгебраїчну
систему з трьох рівнянь:
дають алгебраїчну
систему з трьох рівнянь:
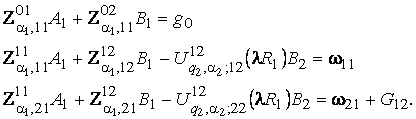 (7)
(7)
У системі (7)
бере участь функція
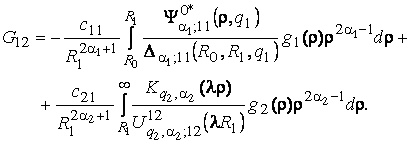
Припустимо,
що виконана умова однозначної розв’язності даної крайової задачі: для
будь-якого ненульового вектора ![]() визначник алгебраїчної
системи (7)
визначник алгебраїчної
системи (7)
![]() (8)
(8)
Визначимо
головні розв’язки крайової задачі (1)-(3):
1) породжені неоднорідністю
крайової умови в точці ![]() функції Гріна
функції Гріна
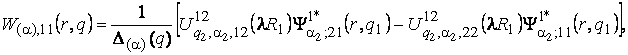
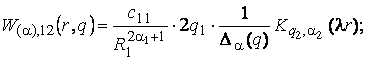 (9)
(9)
2) породжені
неоднорідністю умов спряження функції Гріна
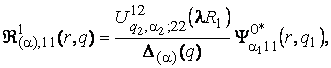
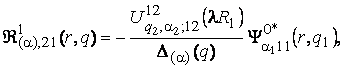 (10)
(10)
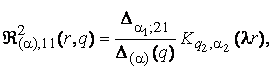
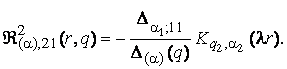
3) породжені
неоднорідністю системи (1) функції впливу
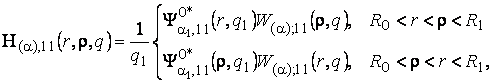
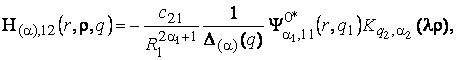
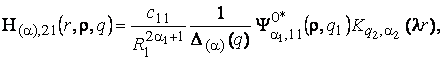 (11)
(11)
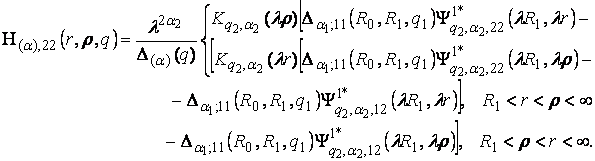
У результаті
однозначної розв’язності алгебраїчної системи (7), підстановки одержаних
значень ![]() у формули (4) маємо
єдиний розв’язок крайової задачі (1)- (3) :
у формули (4) маємо
єдиний розв’язок крайової задачі (1)- (3) :
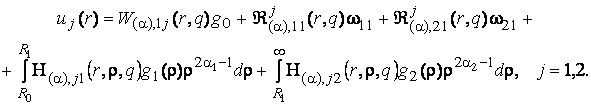 (12)
(12)
Побудуємо тепер
розв’язок крайової задачі (1)-(3) методом гібридного інтегрального
перетворення, породженого на множені ![]() гібридним
диференціальним оператором (ГДО)
гібридним
диференціальним оператором (ГДО)
![]() (13)
(13)
![]() - одинична функція
Гевісайда [3].
- одинична функція
Гевісайда [3].
ГДО ![]() самоспряжений й немає на
множені
самоспряжений й немає на
множені ![]() особливих точок. Тому
його спектр дійсний та дискретний. Цьому спектру відповідає дійсна дискретна
вектор-функція.
особливих точок. Тому
його спектр дійсний та дискретний. Цьому спектру відповідає дійсна дискретна
вектор-функція.
Власні
елементи ГДО ![]() (спектр та спектральну
функцію) знайдемо як розв’язок спектральної задачі Штурма – Ліувілля:
побудувати обмежений на множині
(спектр та спектральну
функцію) знайдемо як розв’язок спектральної задачі Штурма – Ліувілля:
побудувати обмежений на множині ![]() розв’язок сепаратної системи диференціальних рівнянь
Ейлера та Бесселя
розв’язок сепаратної системи диференціальних рівнянь
Ейлера та Бесселя
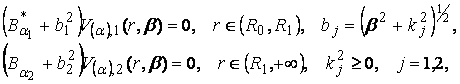 (14)
(14)
за однорідними крайовими умовами
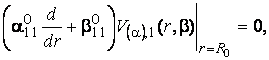
![]() (15)
(15)
та однорідними умовами спряження
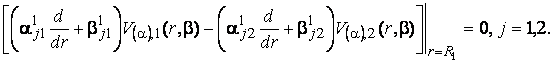 (16)
(16)
Фундаментальну
систему розв’язків для рівняння Ейлера ![]() утворюють функції
утворюють функції ![]() та
та ![]() [1]; фундаментальну
систему розв’язків для рівняння Бесселя
[1]; фундаментальну
систему розв’язків для рівняння Бесселя ![]() утворюють функції
утворюють функції ![]() та
та ![]() [2].
[2].
Якщо покласти
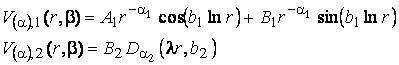 (17)
(17)
то для визначення ![]() крайова умова в точці
крайова умова в точці ![]() й умова спряження (16)
дають однорідну алгебраїчну систему з трьох рівнянь:
й умова спряження (16)
дають однорідну алгебраїчну систему з трьох рівнянь:
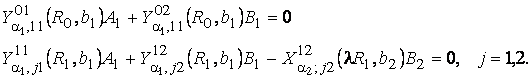 (18)
(18)
Алгебраїчна
система (18) має ненульові розв’язки тоді і тільки тоді, коли її визначник рівний
нулю [4]:
![]() (19)
(19)
Корені ![]() трансцендентного
рівняння (19) утворюють дискретний спектр [5].
Власному
числу
трансцендентного
рівняння (19) утворюють дискретний спектр [5].
Власному
числу ![]() відповідає власна
вектор функція
відповідає власна
вектор функція
![]() (20)
(20)
У рівності
(20) беруть участь функції
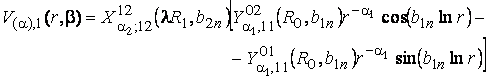
![]() (20)
(20)
Наявність
вагової функції
![]()
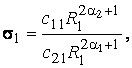
![]() та спектральної вектор-функції
та спектральної вектор-функції
![]() з квадратом норми
з квадратом норми
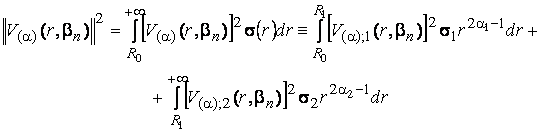
Дозволяє визначити пряме ![]() та обернене
та обернене ![]() скінченне гібридне інтегральне
перетворення [5]:
скінченне гібридне інтегральне
перетворення [5]:
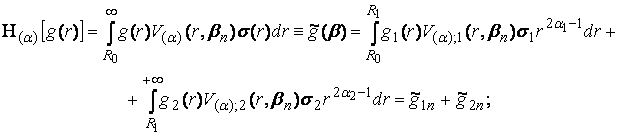 (21)
(21)
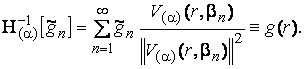 (22)
(22)
Єдиний розв’язок
крайової задачі (1)-(3), побудований за відомою логічною схемою [5], має вигляд:
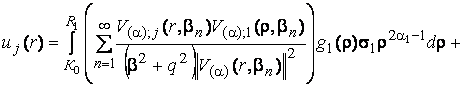
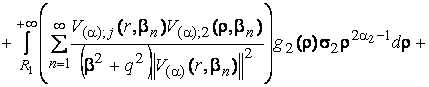 (23)
(23)
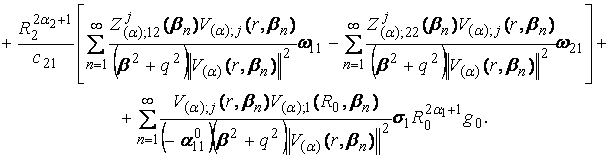
![]()
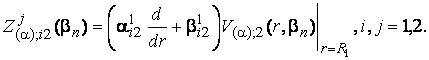
При цьому ![]()
![]() при
при ![]() та
та ![]()
![]() при
при ![]()
Порівнюючи
розв’язки (12) та (23) в силу єдиності, одержуємо наступні формули підсумовування
поліпараметричних функціональних рядів:
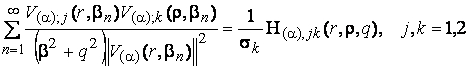 (24)
(24)
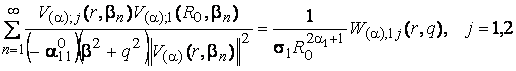 (25)
(25)
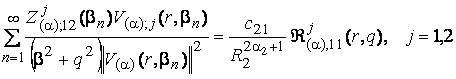 (26)
(26)
 (27)
(27)
Підсумком
викладеного вище є твердження.
Теорема. Якщо вектор-функція ![]() неперервна на множинні
неперервна на множинні
![]() , функції
, функції ![]() задовольняють крайові
умови (2) та умови спряження (3) й
виконується умова (8) однозначної розв’язності крайової задачі (1)-(3), то
справджуються формули (24) – (27) підсумовування поліпараметричних функціональних
рядів за власними елементами ГДО
задовольняють крайові
умови (2) та умови спряження (3) й
виконується умова (8) однозначної розв’язності крайової задачі (1)-(3), то
справджуються формули (24) – (27) підсумовування поліпараметричних функціональних
рядів за власними елементами ГДО ![]() .
.
1.
Степанов В.В. Курс дифференциальных уравнений. – М.:
Физматгиз, 1959. – 468 с.
2.
Ленюк М.П., Міхалевська Г.І. Інтегральні перетворення типу
Конторовича - Лєбєдєва. – Чернівці: Прут, 2002. – 280 с.
3.
Шилов Г.Е. Математический анализ. Второй специальный
курс. – М.: Наука, 1965. – 328 с.
4.
Курош А.Г. Курс
высшей алгебры. – М.: Физматгиз, 1963. – 431 с.
5.
Комаров Г.М., Ленюк М.П., Мороз В.В. Скінченні гібридні
інтегральні перетворення, породженні диференціальними рівняннями другого
порядку . – Чернівці: Прут, 2001. – 228 с.