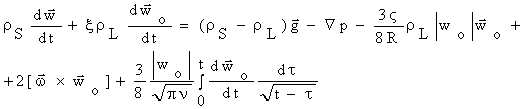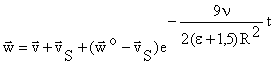ЖУК В.И.

МАТЕМАТИЧЕСКОЕ МОДЕЛИРОВАНИЕ ПРОЦЕССОВ ЗАГРЯЗНЕНИЯ ОКРУЖАЮЩЕЙ СРЕДЫ ПЫЛЕВИДНЫМИ ЧАСТИЦАМИ

Сформулируем следующую гидродинамическую задачу: пусть имеется источник пылевидных частиц, который выбрасывает в окружающую среду частицы определенного размера, формы и плотности и в некоторый момент времени известны скорость и координаты каждой из них. Дальнейшее поведение любой частицы, т.е. зависимость скорости и координат от времени, а также траекторию частицы, можно предсказать на основе анализа независимого движения частицы в несущем потоке. В общем случае на частицу, кроме обычных сил, могут действовать: поле давлений в несущей жидкости (например, при вынужденном течении или механическом перемешивании), силы инерции в неинерциальной системе отсчета (например, при вращении) и другие возможные силы (например, электромагнитные). Уравнение движения одиночной частицы симметричной формы (сферы, протяженного цилиндра, диска) с учетом только гидродинамических сил записывается в виде (1):

(1)

Здесь - скорость движения частицы, - скорость движения частицы относительно несущей среды, - скорость движения несущей среды, - плотность частицы, , n - плотность и вязкость несущей среды, x - коэффициент присоединенной массы (для сферы x=1/2, для поперечно обтекаемого цилиндра x=1, для поперечно обтекаемого диска x=1), R – радиус сферы, цилиндра или диска, - ускорение силы тяжести, Ñp – градиент давления в жидкости, не связанный с действием гравитации, - угловая скорость вращения частицы. Коэффициент гидродинамического сопротивления z выбирается в соответствии с числом Рейнольдса частицы . В уравнении (1) учтены эффект присоединенной массы для сферической частицы, силы тяжести и Архимеда, гидродинамическое сопротивление движению частицы, сила Магнуса, обусловленная эффектом вращения частицы и сила Бассэ, обусловленная нестационарными эффектами и зависящая от предыстории движения частицы. В дальнейшем последними двумя членами в уравнении (1) будем пренебрегать, так как в рамках бесстолкновительной модели вращение отсутствует, а ускорения, испытываемые частицами в обычных условиях, невелики. Последующим этапом решения является определение координат частиц из уравнения (2):

,

(2)

где - радиус-вектор частицы. Для определения вида траектории и скорости движения частицы необходимо задать начальные условия для координат и скорости:

(3)

Решение уравнений (1-3) в общем виде не представляется возможным, так как поле скоростей несущего потока является обычно сложной функцией координат и времени. Теоретический анализ возможен в следующих частных случаях:

1) стационарное течение, когда скорость несущего потока не зависит от времени, и известны профили скорости течения в пространстве. При малых значениях числа Рейнольдса система уравнений может быть проинтегрирована в квадратурах.

2) квазистационарный режим течения, когда изменением скорости несущего потока со временем можно пренебречь.

3) нестационарное течение с однородной в пространстве скоростью. В случае нестационарного потока в среде с пренебрежимо малой вязкостью, когда скорость течения одинакова во всех точках, система допускает решение в аналитическом виде.

В первых двух режимах течения уравнение (1) существенно упрощается и для сферической частицы запишется в виде (4):

(4)

Решение этого уравнения с учетом начальных условий (3) имеет вид (5):

,

(5)

где , - скорость Стокса. Введем понятие времени релаксации, то есть времени, в течение которого скорость можно считать установившейся: . Если время релаксации пренебрежимо мало в сравнении с полным временем движения частицы (t>>t), процесс становится стабильным, при этом скорость движения частицы представляется как результат суперпозиции (наложения) скорости течения и скорости Стокса в виде (6):

(6)

Учитывая, что скорость Стокса направлена к поверхности Земли, расчет траекторий движения частиц в этом случае существенно упрощается. Например, очевидно, что при медленном прохождении вихря над источником загрязнения траектории частиц будут представлять собой спирали, закручивающиеся к поверхности Земли.

В случае нестационарного потока в среде с пренебрежимо малой вязкостью, когда скорость течения одинакова во всех точках, система допускает решение в аналитическом виде.

В более сложных пространственно-временных течениях, например, в случае естественной нестационарной тепловой и концентрационной конвекции в атмосфере, применяются численные методы.

Представленная математическая модель может быть использована для решения численными методами следующих актуальных задач экологии:

прогноз запыленности данной местности с учетом её рельефа, розы ветров, расположения источников загрязнения среды, их параметров и мощности, характера выбросов и других факторов;

анализ распространения радиоактивных частиц в атмосфере вследствие техногенных катастроф, аварий на АЭС и по другим причинам.