ОҚЫТУ ӘДІСТЕМЕСІНДЕ ЕКІНШІ РЕТТІ БЕТТЕРДІ ЗЕРТТЕУ

Тараз мемлекеттік университетінің аға оқытушысы Егемберді Ш.Қ.

Тараз мемлекеттік университетінің М-216 тобының студенті Егенбердиева А.Ә.

Екінші ретті беттерді зерттеу тақырыбы студенттердің осы тақырыпты игеру барысында жоғары ойлау және геометриялық сызбаларды құра білу қабілеттерін талап етеді. Сонымен қатар, геометрия ЖОО – да оқу пәні бойынша дедуктивті, аксиоматикалық негізде білім алу барысында жақсы дамыған теориялық ойлауды талап етеді.

Геометрия оқу пәні ретінде математикадын айырмашылығы тек көлемімен, жүйелілігімен және мағынасының тереңділігімен ғана емес сонымен қатар, қарастырылып отырған сұрақтардың қолданбалы бағытымен ерекшеленеді.

Геометрия әруақытта ғылыммен дамып келе жатқан математика мен математиканың тұрақты өзегі болып табылатын – оқу пәні арасындағы қарама қайшылықты жеңу мақсатында қажетті оқу курсы болып табылады.

Ғылымның дамуы математикалық білімнің мазмұнының үздіксіз дамуын, оқу пәнінің ғылымға жақындауын талап етеді.

Бала жастайынан геометриялық заттармен таныса отырып, көрнекілік ойлау қабілеті мектеп курсына дейін дами бастайды. Оқытушының басты мақсаты геометриялық ойлауды одан ары қарай дамыту болып табылады. Себебі ойлау қабілеті келесі түрдегі күрделі және теңқұқылы процесстерді қамтиды: қабылдау, есте сақтау, танып білу, елестету, тұлғаны толық қанды дамытуға қызмет ететін ойлау қабілеттері.

Геометрияны игерудің басты мақсаты студенттер мен оқушылардың ойлауындағы кеңістіктік елестетуді дамыту болып табылады.

Геометрия курсын тек беттік және кеңістіктік ойлауды қосымша ғана емес, сонымен қатар адамның нақты өмір сүріп жатқан кеңістігінде дағдылану мүмкіндігін дамытатын негізгі функцияларды орындайды. Осы мәселені негізге ала отырып, сабақ үстінде немесе таңдау курстарында білімді тереңдету мақсатында «Екінші ретті беттер» секілді тақырыптарды игеру барысында жүргізілген сабақтар жүйесі ретінде қосымша материалдарды өңдеу пайдалылығы айқын бола бастады.

«Екінші ретті беттер» тақырыбын игеру барысында жүргізілген сабақтар жүйесі келесі мәселелерді шешеді:

- Оқушылар мен студенттердің екінші ретті беттердің теңдеулерін құру және зерттеу бойынша алған білімдерін тереңдету;

- Оқушылардың және студенттердің кеңістіктік ойлауын дамытатын жағдайларды жасау;

- Ақпраттық технологияларды көркемділік үшін және оқушы мен мен студенттердің шығармашылық зерттеуін ұйымдастыру үшін қолдану;

- Оқушыларды және студенттерді компьютерлік математикалық программа Maple-мен жұмыс жасауды үйрету;

- Оқушылар мен студенттерге геометрияға деген қызығушылығын арттыру;

Maple арқылы:

- көптеген функциялардың графигін құру, сонымен қатар әртүрлі типтегі осьтері бар екінші ретті қисықтар мен беттерді (сызықтық және логарифмдік масштабпен);

- декарттық және полярлық координаталар жүйесінде фнкциялардың грфигін құру;

- қолданушының тапсырмасына сай графиктің әртүрлілігі.

Екінші ретті беттерді зерттеу үшін және де олардың графиктерін салу үшін көмектесетін компьтерлік программаларды қарастырайық. Оларға : «MathCAD», «Maple», «Живая геометрия» программалардың математикалық пакеттері, «Advanced Grapher» программалары жатады.

Берілген тақырып кең ауқымды, әрі күрделі болғандықтан, оны игеру қиындыққа соғады. Сондықтан, бұл тақырыпты оқу үшін студенттердің ойлау қабілеті және де геометриялық сызбаларды құру дағдылары жоғары деңгейде болу қажет.

Екінші ретті қисықтар мен беттерді зерттеу қисықтар мен беттердің алгебралық және механикалық теорияларын дамытуға негіз болды. Ол қисықтар: лемнискаталар, конхоидтар, циклоидтар, эпициклойдтар, гипоциклойдтар, кардиоидтар және т.б.

Қисықтар мен беттерді және олардың қасиеттерін зерттеу ғылыми зерттеу жұмыстарына бастау алады.

Екінші ретті беттердің түрін екінші ретті беттердің инварианттары арқылы анықтауға болады. Екінші ретті беттің жалпы теңдеуі түрінде жазылады. Мұндағы тұрақты шамалар параметрлер. Бұл параметрлердің мәндеріне қарай теңдеу әр түрлі бетті және олардың жүйеге қарай әр түрлі орналасуын анықтайды.

Егер жалпы теңдеуді келесі теңдеумен сәйкестендіріп,

және томендегі инварианттарды пайдаланып беттің түрін анықтайық.

, .

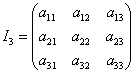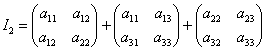
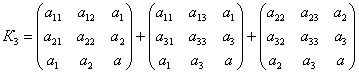, ,(1)

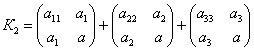
Осындай мақсатпен келесі теңдеумен берілген

екінші ретті беттің түрін анықтап, түзу сызықты жасаушыға перпендикуляр жазықтықпен бетті қиғандағы қимасының параметрін және жасаушыға параллель симметрия жазықтығының теңдеуін жазып, Маple-да зерттейік.

Екінші ретті беттердің канондық түрін анықтау үшін жоғарыдағы формулаларды пайдаланып,

(1) формуланы пайдаланып, келесі канондық теңдеуді аламыз:

яғни

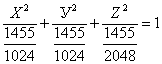(2)

(2) теңдеу жарты осьтері болатын элипсоид болады.

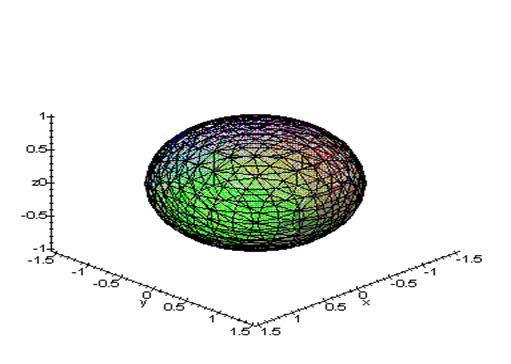
Екінші ретті беттің түрін анықтап болған соң, табылған эллипсоидтың графигін координата жүйесінде салайық:

Әдебиеттер

1. Бескоровайная Л. С., Перекатьева О. В. Методика современного открытого урока математики. – Ростов-на-Дону, 2003.

2. Бурменская Г. В., Карабанова О. А., Лидерс А. Г. Возрастно-психологическое консультирование: Проблемы психического развития детей. – М., 1990.

3. Метельский Н. В. Пути современного обучения математики. – Мн., 1989.

4.А.Д. Александров, Н.Ю. Нецветаев, Геометрия. «Наука» Физматлит, 1990., 32-53

5. Новосельцева З.И. Развернутые планы лекций и учебные задания для студентов по курсу "Теоретические основы обучения математике"/ С.-Петербург, Изд-во "Образование", РГПУ, 1997

6. Методика преподавания математики в средней школе : Общая методика; Учебное пособие для студентов физико-математического факультета педагогических институтов / В.А. Оганесян, Ю.М. Колягин, Г.Л. Луканкин, В.Я. Саннинский, -2-е издание переработано и дополнено / М., Просвещение ,1980.

7. Ильин В. А., Позняк Г. Аналитическая геометрия. – М.: Наука, 1974

8. Ефимов А. В., Демидович Б. П. Сборник задач по математике для ВТУЗов (4 части). – М.: Наука, 1993