К.т.н. Лавренко Я.І., Яковлєва С.І.

Національний технічний університет України

«Київський політехнічний інститут», Київ, Україна

ДОСЛІДЖЕННЯ ЗАЛЕЖНОСТІ ПРОГИНІВ ТРИШАРОВИХ ПЛАСТИНИ ПРИ РІЗНИХ МОДУЛЯХ ПРУЖНОСТІ

В наш час відбувається стрімкий розвиток відновлюваних джерел енергії. Серед них одною з найбільш розповсюджених є сонячна енергія. Сонячні батареї зазвичай підлягають значним навантаженням внаслідок зміни погодних умов. Це можуть бути як навантаження внаслідок вітру чи опадів, так і циклічні денні чи сезонні зміни температури. Це може призводити до порушення герметичності між шарами, утворенню тріщин в крихких матеріалах і, як наслідок, до зниження ефективності. Тому чисельне моделювання та дослідження поведінки окремих шарів, як і всієї пластини, є необхідним та дуже актуальним питанням сьогодення [1, 2]. Сонячні модулі, як правило, мають наступну будову: зовнішні шари зі скла та внутрішні – м’яких полімерних шарів, які виконують захисну функцію для дуже тонких та крихких кремнієвих сонячних панелей.

Чисельне моделювання було проведено за допомогою програмного пакету ABAQUS в інституті механіки Отто-фон-Геріке Університету Магдебурга (Німеччина). В даній задачі припускається, що всі шари композиту можуть довільно провертатись та переміщуватись в площині.

Розрахунки показали, що збільшення чи зменшення максимального прогину для різних сіток залежить від модуля пружності середнього шару. Тобто при більшому модулі пружності прогин балки зростає зі згущенням сітки. На рисунку 1 показані результати дослідження збіжності при різних модулях пружності середнього шару.

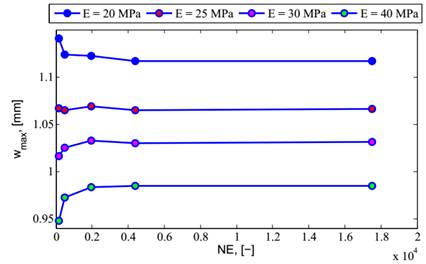
Рис. 1. Збіжність пригонів пластини

при різних модулях пружності середнього шару

На графіках (рис.2) зображені повздовжні переміщення в центрі пластини u₁ та u₂ для всіх трьох шарів при температурах +23, +80 та -40 °С.

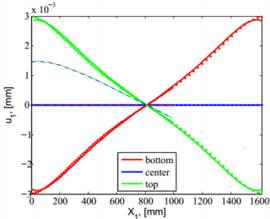
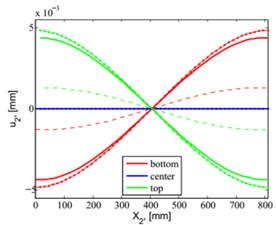
Рис. 2. Повздовжні переміщення u₁(зліва) та u₂ (справа) при Т = +23 °С (суцільна лінія), Т = +80 °С (пунктирна лінія) та Т = -40 °С (штрих-пунктир)

Порівнюючи з наявними результатами на основі extended layerwise theory (рис.3), видно, що значення переміщень, розрахованих continuum shell elements, в десять раз перевищують наявні.

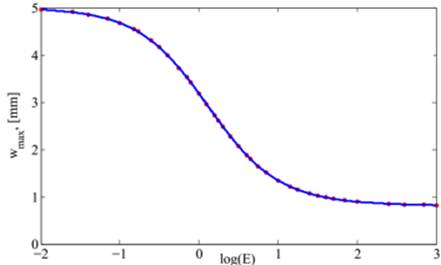
Рис. 3. Залежність максимального прогину балки від модуля пружності середнього шару

На графіку зображена логарифмічна залежність максимального прогину пластини від модуля пружності середнього шару. Ця залежність відображає реальну поведінку сонячного модуля за різних температур. При цьому різні значення модуля пружності відповідають різним температурам навколишнього середовища. При низьких температурах модуль пружності збільшується, тобто середній шар стає більш жорстким, а вся пластина більш однорідною. Відповідно, прогин в даному випадку зменшується. При меншому модулі пружності, тобто за високих температур, навпаки, прогин збільшується.

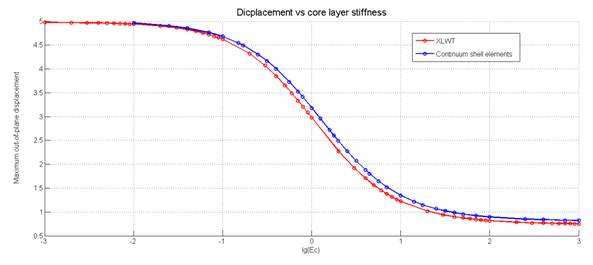
Рис. 4. Порівняння результатів

З рисунку 4 видно, що збіжність результатів обох теорій досить висока. Це значить, що використана в даній задачі модель адекватно описує поведінку сонячних батарей.

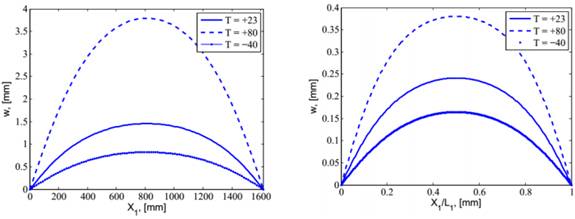
Рис. 5. Прогини пластини за різних температур при використанні continuum shell elements (зліва) та extended layerwise theory (справа)

Розподіл прогинів в обох випадках симетричний (Рис.5), має місце однакова тенденція (прогин зростає зі збільшенням температури). З одного боку, це говорить про правильність розрахунків. Проте варто відмітити, що значення прогинів при застосуванні просторових оболонкових елементів в 10 раз перевищують значення прогинів XLWT.

Висновки

В подальшому в роботі планується провести дослідження використаного скінченного елемента. Необхідно також з’ясувати, яка теорія механіки закладена в даному елементі та чи є вона коректною для описання поведінки анти-сендвіча. Крім того, необхідно з'ясувати причини великої різниці в результатах обох розрахунків та неправильної збіжності.

Список використаних джерел:

1. K. Naumenko und V. A. Eremeyev, „A layer-wise theory for laminated glass and photovoltaic panels―, Compos. Struct., Bd. 112, Nr. 1, S. 283–291, 2014.

2. S.-H. Schulze, M. Pander, K. Naumenko, und H. Altenbach, „Analysis of laminated glass beams for photovoltaic applications―, Int. J. Solids Struct., Bd. 49, Nr. 15–16, S. 2027–2036, 2012.