Юрій Борисович Прібилєв
(докторант кафедри)
Національний університет оборони України імені Івана
Черняховського, м. Київ, Україна
УДОСКОНАЛЕНИЙ МЕТОД ЗАБЕЗПЕЧЕННЯ МЕТРОЛОГІЧНОЇ НАДІЙНОСТІ
ВИМІРЮВАЛЬНИХ КАНАЛІВ КОНТРОЛЬНО-ВИПРОБУВАЛЬНИХ СТАНЦІЙ
У статті описаний удосконалений метод забезпечення
метрологічної надійності вимірювальних каналів контрольно-випробувальних
станцій, що ґрунтується на алгоритмі, який дозволяє здійснити оптимальний вибір
параметрів радіоелементів.
Ключові
слова: метрологічна надійність, контрольно-випробувальна станція, метод
Хука-Дживса.
Найбільш
кардинальним шляхом розвитку Збройних Сил України є прийняття на озброєння
нових зразків озброєнь та військової техніки (ОВТ). Однак, у цьому випадку при
обмеженому фінансуванні військово-промислового комплексу України темпи
оновлення ОВТ можуть відставати від їх темпів старіння. Особливо це стосується
високотехнологічних та високовартісних видів озброєнь, до яких відносяться
засоби протиповітряної оборони (ППО). Тому у короткостроковій перспективі є доцільним і практично
застосовується інший шлях підвищення технічної готовності ОВТ ППО – це
проведення ремонту та модернізація існуючих зенітно-ракетних комплексів (ЗРК)
[1].
Для
підтримання технічної готовності модернізованих ЗРК необхідним є проведення
регламентних та контрольно-випробувальних робіт з ракетним озброєнням (РО). Для
цього призначені штатні контрольно-випробувальні станції (КВС), які є
обов’язковою складовою частиною ЗРК, та які також повинні бути модернізованими
одночасно з ЗРК [2]. Як правило, при модернізації ЗРК відбувається заміна
елементної бази електронного обладнання, контроль параметрів якого вимагає
проведення вимірювань з меншими похибками.
Підвищення
вимог до точності вимірювань параметрів РО має наслідком застосування якісно
нових за фізичними і конструктивно-технологічними ознаками елементів, та
ускладнення КВС. Але ускладнення КВС, як правило, супроводжується зменшенням їх
надійності. Для КВС, в основі роботи яких є вимірювання параметрів РО, важливе
значення має метрологічна надійність (МН), яка характеризує вимірювальні канали
КВС, перш за все – як засоби вимірювань. МН визначає здатність КВС зберігати
встановлені значення метрологічних характеристик (МХ) визначений час при
нормальних умовах експлуатації.
Від якості КВС, зокрема, від їх МН та стабільності характеристик, значною
мірою залежать оперативність, необхідні точність і достовірність інформації про
технічний стан РО, що одержувані з їх допомогою. Тому модернізація КВС та покращення їх якісних характеристик, а саме –
забезпечення заданого рівня МН вимірювальних каналів КВС є актуальною
проблемою. Розробленням та удосконаленням теорії МН займались багато вчених. У
роботах А. Е. Фрідмана [3], Т. І. Чернишової [4],
М. Ю. Яковлева [5, 6, 7] закладено наукову основу,
теоретичні та методологічні передумови подальшого розвитку методів підвищення
МН засобів вимірювальної техніки. Але питання забезпечення заданого рівня МН
при проектуванні КВС з урахуванням їх специфіки у цих роботах не розглядались.
У [8]
запропонований метод підвищення МН, який оснований на виборі оптимальних
параметрів структурних елементів засобів вимірювальної техніки (ЗВТ). Цей метод
прийнятий за базовий при розробці удосконаленого методу забезпечення МН
вимірювальних каналів КВС. Метою статті є розробка удосконаленого методу
забезпечення МН вимірювальних каналів КВС.
Метод, який розроблений у [8], забезпечує необхідні значення показників
МН та ґрунтується на виборі оптимальних параметрів структурних елементів ЗВТ на
етапі проектування. Цей метод дозволяє, не змінюючи структури проектованого
ЗВТ, здійснювати оптимальний вибір параметрів комплектуючих елементів. Розглянемо
основні положення цього методу. Серед показників МН вибраний найбільш придатний
для практичного застосування показник – напрацювання до метрологічної відмови.
Завдання забезпечення максимальної МН ЗВТ сформульовано у вигляді задачі пошуку
максимального напрацювання до метрологічної відмови структурного елемента ЗВТ,
що має найменший рівень МН:
, (1)
де 
, 
– сукупність МХ;
– вектор зовнішніх чинників, що
впливають на ЗВТ;
– область працездатності;
– область значень зовнішніх чинників.
Відповідно, завдання забезпечення необхідного рівня МН ЗВТ представлено у
вигляді завдання забезпечення заданого напрацювання до метрологічної відмови
ЗВТ. З урахуванням того, що дрейф МХ обумовлений змінюванням у часі параметрів
елементної бази ЗВТ, рішенням поставленого вище завдання є деяка сукупність
параметрів комплектуючих елементів. Причиною метрологічних відмов є старіння і
знос елементної бази ЗВТ, тому за характером метрологічні відмови є поступовими.
Оцінювання МХ, які досліджуються, виконується за допомогою методів імітаційного
моделювання (за умови відсутності статистичної інформації) за значеннями
випадкових величин параметрів у різні моменти часу. На підставі отриманих
параметрів у результаті оцінювання МХ, здійснюється прогнозування дрейфу МХ ЗВТ
шляхом екстраполяції побудованих математичних моделей дрейфу на область
прогнозу. Далі шляхом заміни найбільш ненадійних з точки зору МН елементів ЗВТ
здійснюється підвищення їх напрацювання до метрологічної відмови.
Розглянутий метод підвищення МН враховує основну причину, що призводить
до метрологічної відмови – це нестаціонарний випадковий процес зміни у часі
нормованої МХ з математичним очікуванням і дисперсією, які монотонно змінюються
у часі. Головною причиною зміни МХ у часі є процеси старіння елементної бази
ЗВТ, що відбуваються на молекулярному рівні. При цьому домінуючим чинником, що
визначає старіння ЗВТ, є календарний час, що минув з моменту виготовлення ЗВТ,
а не час експлуатації у включеному стані.
Стабільність електрорадіоелементів (ЕРЕ) залежить від швидкості процесів
їх старіння. У запропонованому методі [8] використовується простий та логічний
спосіб підвищення МН ЗВТ – вибір ЕРЕ, які зроблені з матеріалів, що
забезпечують найбільш стабільні характеристики ЕРЕ у часі. Це є головним, але
не єдиним чинником, що визначає рівень МН ЗВТ. У [9] вказано, що на рівень МН
ЗВТ мають вплив схемотехнічні особливості та електричні режими роботи
функціональних блоків, які складають ЗВТ.
Наприклад, вибір типу підсилювача та його схемотехнічне рішення (вибір
номіналів резисторів, що задають режим роботи транзистора у каскаді підсилення)
у складі вимірювального перетворювача також безпосередньо впливають на дрейф
основної нормованої МХ – чутливості вимірювального перетворювача. Для
врахування впливу зазначених чинників на рівень МН розглянутий вище метод
підвищення МН необхідно удосконалити.
Виконання завдання забезпечення необхідного рівня МН вимірювальних
каналів КВС буде вирішено, якщо буде забезпечений необхідний час напрацювання
до метрологічної відмови вимірювального каналу 
, який регламентується замовником в технічних вимогах до КВС:
.
(2)
Це завдання формалізовано виразом (1) та реалізовано у вигляді алгоритму,
який побудований зі застосуванням методу прямого пошуку Хука-Дживса [10]. Цей
метод був розроблений ще у 1961 році, але до сьогодні є дуже поширеним,
оскільки ефективно вирішує завдання пошуку безумовного локального екстремуму
функції багатьох змінних і відноситься до прямих методів, тобто спирається
безпосередньо на значення функції. Метод Хука-Дживса може бути використаний при
вирішенні задачі оптимального вибору номіналів параметрів комплектуючих ЕРЕ,
які найбільше впливають на напрацювання до метрологічної відмови вимірювальних каналів КВС.
Реалізація цього методу при розробці програмного забезпечення не є складною
задачею та дозволить автоматизувати процедуру розрахунку номіналів параметрів
ЕРЕ при проектуванні вимірювальних каналів КВС.
Згідно цього методу, пошук екстремуму цільової функції (напрацювання до
метрологічної відмови) складається з послідовності кроків досліджуючого пошуку
коло базисної точки, за умови успішності якого здійснюється пошук за зразком. Метод Хука-Дживса складається
з двох етапів: пробного пошуку та пошуку за зразком. Задається початкова точка 
, яка відповідає
початковому значенню номіналу параметру ЕРЕ, а також початковий крок зміни 
. Здійснюється
обчислення значення цільової функції 
в стартовий точці. Далі по черзі змінюється
кожна змінна (при фіксованих інших) на обрані значення , та кожен раз
розраховується значення цільової функції. Якщо цільова функція не покращується
(час напрацювання на метрологічну відмову – збільшується), напрямок пошуку
замінюється на протилежний.
Наприклад, 
збільшуємо на 
: 
. Якщо цей крок не збільшує 
, робимо протилежний крок – зменшуємо на : 
. Якщо і цей крок також не збільшує , фіксуємо змінну (номінал параметра
ЕРЕ) та починаємо змінювати наступну змінну: 
змінюємо на 
у двох напрямках по
черзі. Таким чином досліджуємо усі змінні (обрані параметри ЕРЕ).
Після завершення пробного пошуку застосовується стратегія пошуку за зразком, яка продовжує максимізацію цільової функції у напряму, що визначений пробним пошуком.
Успішні варіації змінних у пробному пошуку (тобто ті варіації змінних, які збільшили
цільову функцію) визначають вектор, який вказує локальний напрямок оптимізації.
Проводиться серія кроків уздовж цього вектору, які збільшуються до тих пір,
поки цільова функція зменшується при кожному такому кроці. Довжина кроку пошуку
за зразком зазвичай обирається
пропорційно числу вдалих кроків, що мали місце раніше у цьому координатному
напрямку. Величина кожного наступного кроку задається прискорюючим множником.
Той факт, що даний алгоритм володіє властивістю прискорюватися, сприяє
підвищенню його загальної ефективності. Друга перевага методу Хука-Дживса –
можливість отримання за його допомогою наближеного рішення, якість якого
підвищується на всіх стадіях чисельного рішення.
Розглянутий метод Хука-Дживса використаний для вирішення завдання підвищення
МН за критерієм максимуму напрацювання до метрологічної відмови, та наведений у
вигляді алгоритму на рис. 1.
Алгоритм має наступні кроки.
1. Спочатку водяться номінали ЕРЕ принципової схеми вимірювального каналу КВС.
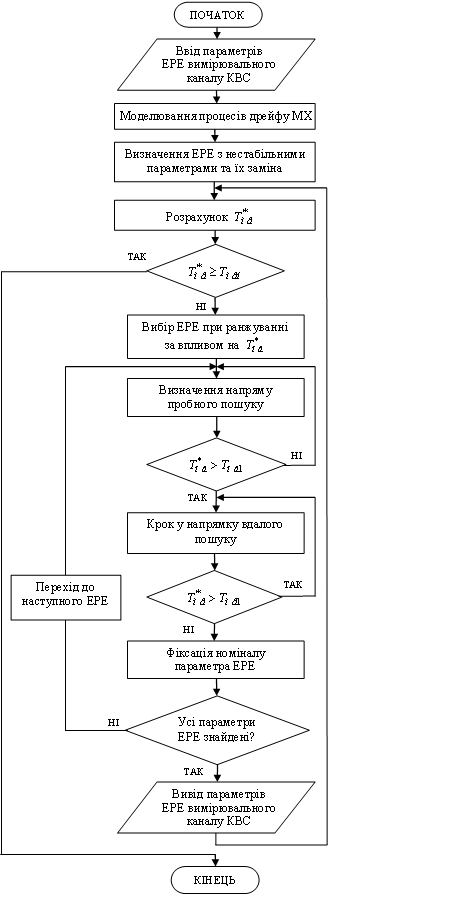
Рис.1. Схема алгоритму забезпечення МН вимірювальних каналів КВС
2. Далі проводиться моделювання процесів дрейфу МХ на основі збору
та аналізу вихідної інформації про вимірювальні
канали КВС: інструкцій з експлуатації,
технічного опису, технічних умов, даних про елементну базу принципових схем і
дрейфу параметрів ЕРЕ. Метрологічні відмови вимірювальних каналів КВС є поступовими внаслідок старіння і зносу
елементної бази, тому значення МХ, що досліджуються, можуть бути визначеними з
використанням інформації про аналоги або за допомогою методів імітаційного
моделювання (при відсутності статистичної інформації) за значеннями випадкових
величин параметрів у різних часових перерізах.
3. Шляхом заміни найбільш ненадійних з точки зору МН ЕРЕ принципових
схем вимірювальних каналів КВС здійснюється підвищення їх напрацювання до метрологічної відмови.
4. На підставі даних, отриманих в результаті моделювання дрейфу МХ вимірювальних каналів КВС,
шляхом екстраполяції побудованих математичних моделей дрейфу МХ на область прогнозу
вирішуються завдання прогнозування МН та проводиться розрахунок показника МН – 
[8].
5. Проводиться перевірка забезпечення необхідного рівня МН вимірювальних каналів КВС. Якщо
необхідний час напрацювання до метрологічної відмови вимірювальних
каналів КВС менше за потрібного, проводиться схемотехнічна оптимізація роботи вимірювального каналу КВС методом знаходження номіналів ЕРЕ принципових схем вимірювального каналу КВС, що впливають на дрейф МХ та на рівень МН.
6. Визначається сукупність ЕРЕ методом ранжування ЕРЕ за їх впливом
на МН вимірювального каналу КВС. Виділяються ЕРЕ в кожному вимірювальному
каналі КВС, збільшення або зменшення
номіналів яких викликає зміну МХ більше визначеного рівня. Обраний критерій
враховує не тільки вплив номіналів ЕРЕ на дрейф МХ вимірювальних каналів КВС, але і враховує вплив їх дисперсії
(відхилення номіналів ЕРЕ від середнього значення).
7. Проводиться вибір напрямку пошуку та здійснюється пробний пошук в
обраному напрямку з визначеним кроком: 
.
8. Математичним моделюванням дрейфу МХ перевіряється успішність
вищезазначеного кроку: 
. При негативному результаті (час напрацювання на
метрологічну відмову зменшився) напрямок пошуку змінюється на протилежний: 
.
9. Робиться цикл кроків у вдалому напрямку.
10. Після кожного кроку перевіряється його
успішність (збільшення більше заданого граничного рівня).
11. Якщо наступний крок не є успішним, цикл завершується та
оптимізація параметра ЕРЕ закінчується – номінал ЕРЕ фіксується.
12. Далі переходять до оптимізаційного циклу (7 – 11 кроки
алгоритму) для іншого ЕРЕ, який був обраним на шостому кроці алгоритму.
13. Після перебору усіх обраних ЕРЕ наприкінці роботи алгоритму
здійснюється вивід їх номіналів, вибір яких при проектуванні зможе забезпечити
необхідний час напрацювання до метрологічної відмови вимірювальних каналів КВС.
Таким чином, у статті розглянутий удосконалений метод забезпечення МН
вимірювальних каналів КВС, що ґрунтується на алгоритмі, який дозволяє здійснити
оптимальний вибір параметрів ЕРЕ. На відміну от існуючого методу [8],
запропонований метод дозволяє зменшити дрейф МХ, що обумовлений як часовою
зміною параметрів елементної бази, так і схемотехнічними рішеннями при
проектуванні вимірювальних каналів КВС, а саме – оптимальним вибором номіналів
ЕРЕ вимірювальних каналів КВС.
Слід зауважити, що підвищення МН за рахунок вибору ЕРЕ, які мають стабільні характеристики
[8], у більшості випадків досягається використанням у їх складі дорогоцінних
металів, що є затратним та не завжди виконує умову обмеження на вартість при
проектуванні. Запропоноване удосконалення методу дозволяє комбінаторним
способом підвищити МН вимірювальних каналів КВС без збільшення їх вартості.
Список
літератури
1. Карпенко Д. В. Стан та перспективи розвитку зенітного
ракетного озброєння Повітряних Сил Збройних Сил України. / Наука і техніка
Повітряних Сил Збройних Сил України, 2017, № 2(27) С.75 - 78.
2. Бурковский С. И.
Сравнительная оценка эффективности зарубежных вариантов модернизации ЗРК
С-125М1 “Печора-М1” при решении задач ПВО важных
государственных объектов Украины. [Текст] / С. И. Бурковский,
П. Ю. Седышев // Системи
озброєння і військова техніка. – 2010. – № 1(21). – С. 36 - 44.
3. Прібилєв Ю. Б.
Підхід до побудови уніфікованої універсальної автоматизованої
контрольно-випробувальної станції ракетного озброєння / Ю.Б.Прібилєв,
Л.В. Сакович. // Наука і оборона. – №1, 2017. – С. 42 - 48.
4. Фридман А. Э.
Метрологическая надежность средств измерений и определение межповерочных
интервалов / Фридман А.Э. // Метрология. – 1991. – № 9 – С. 52 - 61.
5. Чернышова Т. И.
Метрологическая надёжность средств неразрушающего контроля теплофизических
свойств материалов и изделий : дис. ... доктора техн. наук: 05.11.13 /
Чернышова Т. И. – Тамбов, 1995. – 196 с.
6. Яковлев М. Ю.
Метрологическая надёжность средств измерительной техники / М.Ю. Яковлев // Зб.
наук. пр. НТУ “ХПІ”.– 2005. – Вип. 37. – С. 187 - 191.
7 Яковлев М.
Ю. К вопросу об оценке метрологической надёжности средств измерительной техники
авиационных радиотехнических систем / М.Ю. Яковлев, Ю.Б Прибылев,
А.П. Волобуев // Радиоэлектронные и компьютерные системы. – 2006. – Вып. 7
(19). – С. 143 - 146.
8. Яковлев М. Ю.
Розвиток теорії метрологічної надійності засобів вимірювальної техніки
військового призначення: дис. ... доктора техн. наук: 05.01.02 / Яковлев Максим
Юрійович. – Львів, 2011. – 425 с.
9. Кузнецов В. А.
Вопросы обеспечения метрологической надежности средств измерений /
В.А. Кузнецов // Измерительная техника. – 1984. – № 1. – С. 8 - 10.
10. А.В. Аттетков,
С.В. Галкин, B.C. Зарубин. Методы оптимизации: Учеб. для вузов / Под
ред. B.C. Зарубина, А.П. Крищенко. — 2-е изд., стереотип. — М.: Изд-во МГТУ им.
Н.Э. Баумана, 2003. – 440 с.
Прібилєв Юрій Борисович – кандидат технічних наук,
доцент, докторант кафедри застосування космічних систем та геоінформаційного
забезпечення інституту інформаційних технологій Національного університету
оборони України імені Івана Черняховського.
тел. 096-903-10-03