Математика/1. Дифференциальные и интегральные уравнения

Ефремов А.А.

Могилёвский государственный областной

институт развития образования, Беларусь

Решение функциональных уравнений

методом сдвига аргумента

На сегодняшний день тема «Функциональные уравнения» является неотъемлемой частью любого курса по «олимпиадной» математике. Специфика её, на мой взгляд, заключается в следующем.

Во-первых, эта тема по большому счёту «оторвана» от реальной практики. Скорее, это как раз то, что можно назвать «математикой для математики». Функциональные уравнения в своё время использовали, например, Д’Аламбер (для обоснования закона сложения сил) и Лобачевский (для выведения формулы угла параллельности в неевклидовой геометрии).

Во-вторых, тема тесно связана с высшей математикой. Некоторые функциональные уравнения невозможно решить без предельного анализа, знания дифференциальных уравнений и т.п.

В-третьих, здесь в отличие от многих других разделов «олимпиадной» математики есть достаточно чётко очерченный круг применяемых приёмов и методов. Так, в настоящее время для решения функциональных уравнений в элементарной математике широко применяются два метода: замена переменной и метод частных значений.

Ни в одном известном мне источнике не выделяется метод, о котором пойдёт речь в данной статье. В некотором смысле метод «сдвига» аргумента можно считать частным случаем метода замены переменной, однако ему присущи некоторые отличительные особенности.

Метод «сдвига» можно было считать только одним из специфических приёмов решения уравнений с функциями, но он встречается не в одной и не в двух задачах на соревнованиях различного уровня, причём на протяжении всего пути исторического развития математической мысли. Именно поэтому, по моему убеждению, возникает необходимость его выделения и обобщения.

Рассмотрим алгоритм применения описанного метода на конкретных примерах.

Пример 1 (Беларусь, 1994). Докажите, что не существует функции , удовлетворяющей системе уравнений:

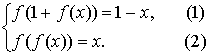
Решение.

Обозначим и сложим уравнения системы. Получим

.

Выполним сдвиг аргумента . Уравнение примет вид

Из (3) и (4) ясно, что .

Воспользуемся соотношением (2). Значения функции при равных значениях аргумента должны совпасть:

– противоречие. Таким образом, функции , удовлетворяющей исходной системе не существует.

Пример 2 (СССР, 1968). Функция , определённая при всех действительных значениях аргумента и принимающая действительные значения, при всех x удовлетворяет условию . Докажите, что функция периодическая и найдите её период.

Решение. Ошибочно было бы начинать решение с определения периодической функции. В таких задачах гораздо эффективнее сначала найти (подобрать) период, а затем уже делать вывод о периодичности. Исходное уравнение равносильно системе

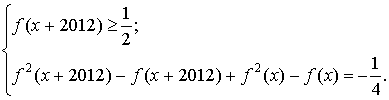
Выполним сдвиг аргумента :

Почленно вычтем из этого уравнения второе уравнение системы. Имеем:

.

Из первого уравнения системы можно сделать вывод, что функция ни при каком аргументе не принимает значений меньше . Поэтому возможен только один случай: . Легко показать, что функция периодическая с периодом 4024.

Пример 3 (США, 2010). Найдите все пары многочленов и с действительными коэффициентами такие, что

. (*)

Решение. Сразу же выполним сдвиг аргумента . Получим:

(**)

Вычитая из равенства (*) равенство (**), получим

Из условия ясно, что, во-первых, многочлены и тождественно не равны нулю, а во-вторых, они не могут иметь общего непостоянного множителя. Поэтому можно заключить, что многочлен делится без остатка на . Так как степени этих многочленов равны, а каждый коэффициент первого вдвое больше соответствующего коэффициента второго, то

.

Последнее выражение можно записать в виде

.

Форма записи подсказывает, что следует ввести функцию . Тогда . Можно утверждать, что может быть только константой. Повторяя аналогичные рассуждения для , в конечном итоге получим, что исходное соотношение имеет место для всех линейных многочленов и . Особо отметим, что коэффициенты этих многочленов должны в обязательном порядке удовлетворять условию .

В заключение постараемся выделить общие черты рассмотренных задач. Предпосылками применения метода сдвига аргумента являются следующие ситуации:

а) в правой части функционального уравнения находится константа, которая никак не изменится при операции сдвига;

б) левая часть представляет собой некоторую комбинацию значений одной и той же функции, только с разными аргументами (которые, в свою очередь, отличаются на постоянную величину);

в) сдвиг осуществляется таким образом, что один из наличествующих аргументов «переходит» в другой.

Хочется верить, что выделение метода сдвига аргумента позволит более глубоко понять теорию функциональных уравнений и поможет эффективно решать научно-практические задачи.

Литература:

1. Морозова, Е.А. Международные математические олимпиады. Задачи, решения, итоги. // Пособие для учащихся. 4-е изд., испр. и доп. М. : Просвещение, 1976. – 288 с.

2. Барабанов, Е.А. Задачи Белорусской математической олимпиады школьников (1994 г.). / Е.А. Барабанов, В.И. Берник, И.И. Воронович, С.А. Мазаник. // Сборник задач. Мн. : АН Беларуси. Институт математики, 1995. – 103 с.