Терновых И.И.
Воронежский
Государственный Университет
Факультет
Прикладной математики, информатики и механики
Кафедра
вычислительной математики и прикладных информационных технологий
Устойчивость решений
нечеткой динамической системы. Плотность нечеткого множества и устойчивость.
Рекомендовано
к публикации профессором Леденевой Т.М.
Введение
В настоящее время практическая значимость
нечетких моделей очень велика, так как они позволяют описывать динамику сложных
процессов, не поддающихся точному количественному анализу и, как следствие,
разрешению их традиционными алгоритмами. Под
динамической системой будем понимать систему, описывающую процесс перехода от
одного состояния в другое. Динамическую систему с дискретным временем назовем
дискретной динамической системой (ДДС). Если состояния системы характеризуются
неопределенностью, имеющей характер нечеткости, то, описывая их с помощью
нечетких подмножеств в пространстве входных переменных, получим нечеткую ДДС.
Для таких систем необходимо учитывать понятие устойчивости, поскольку это позволяет сформировать
необходимые управляющие воздействия. Без исследования устойчивости решений
нечетких дискретных систем анализ нечеткой дискретной модели не может быть
полным. В статье вводится величина, характеризующая плотность нечеткого
множества, которая позволяет определить устойчивость решений нечеткой ДДС на
основе известного понятия устойчивости по Ляпунову.
Нечеткие дискретные динамические системы. Плотность решений
нечеткой дискретной динамической системы
Под
динамической системой будем понимать систему, описывающую процесс перехода из
одного состояния в другое, при условии, что ее начальное состояние известно. В
системах с дискретным временем поведение системы описывается последовательностью состояний.
Нечеткую
дискретную динамическую систему можно описать выражением следующего вида
,
(1)
где «
» – оператор максминной композиции; 
– нечеткие
состояния, которые, по сути, являются нечеткими подмножествами множества 
, т.е. 
; 
, которое задает закон, по которому система переходит из
состояния 
в 
.
Если
множество 
конечно (
, то нечеткое отношение R может
быть представлено матрицей:
, где 
.
С
учетом определения «
» и в случае, если 
(2.1) можно
переписать в виде:
,
где 
– вектор-функции
принадлежности нечетких состояний 
нечеткого множества 
в моменты времени 
соответственно.
В
качестве количественной характеристики нечеткого множества будем рассматривать
его плотность.
Определение 1. Пусть 
- нечеткое
подмножество 
с функцией
принадлежности 
. Тогда плотностью нечеткого множества 
будем называть
величину
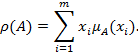
Пусть 
- нечеткие
подмножества универсального множества 
. Тогда плотность 
обладает следующими
свойствами:
1)
Если 
, т.е. 
, тогда 
;
2)
Если 
, т.е. 
, то 
;
3)
Пусть 
- бинарное
отношение на 
, тогда, если 
, то 
, и, следовательно, 
.
Применим
формулу плотности нечеткого множества к системе (1):
(2)
Так
как для дискретной динамической системы
, то из
нижеследующих формул получим следующее:
,
,
.
Тогда
представим (2) следующим образом:
.
(3) Рассмотрим пример. Пусть
нечеткое отношение 
задано матрицей
следующего вида: 
,
В
качестве начальных значений возьмем:
,
.
Для
различных значений 
вычислим 
по формуле (2), а
затем для полученного вектора найдем плотность по формуле (3).
На
рис.1 line1, line2 представляют собой графики плотности для
начальных состояний 
, 
соответственно.
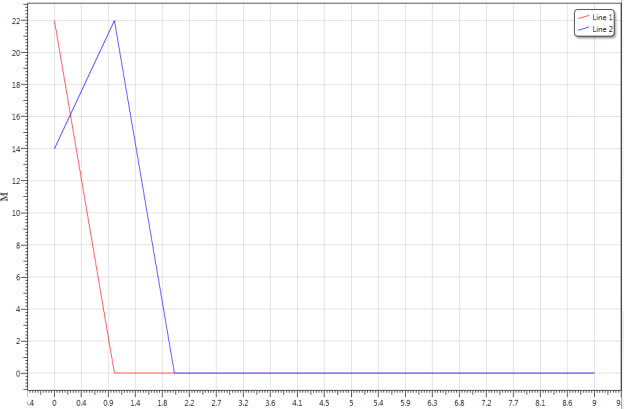
Рисунок 1
Таким
образом, видно, что, начиная с некоторого состояния, система ведет себя
устойчиво.
Обозначим
приращение плотности для следующих друг за другом состояний в виде:
.
Определение 2. Решение
системы (2) устойчиво и не зависит от начального положения, если 
, иначе решение системы (1) является неустойчивым.
Список литературы
1.
Glas M. Theory of fuzzy systems/Glas M.//Fuzzy sets and systems. – 1983.
– 10. – P. 65-77
2.
Е.В. Ивохин, С.О.Волчков. Исследование динамики нечетких дискретных систем/ Е.В. Ивохин, С.О.Волчков//System research & Information
Technologies. – 2005. – 4. – P. 94 – 105
3. Леденева Т.М. Обработка
нечеткой информации. – Воронеж.:ВГУ, 2006. – 233 с.
4. Сборник задач по дифференциальным уравнениям / Под ред.А.Ф.
Филиппова. – М.: Издательство ЛКИ, 2008. – 240 с.