Компьютерное моделирование идеальной модели зубочелюстной системы

Зубочелюстные аномалии отражаются на гармонии лицевого скелета, их следствием могут быть эстетические отклонения и развитие пародонтоза. Перед лечением зубочелюстных аномалий специалист, в зависимости от характера заболеваний строит предварительный прогноз изменения зубных дуг пациента.

Задача состоит в разработке программного обеспечения, которое моделирует трехмерную модель зубочелюстной системы пациента после планируемого лечения. В основе программного обеспечения лежит разработанный автором алгоритм построения «идеальной» параметрической модели зубных дуг пациента. В ходе исследования рассматриваются пациенты европейского типа с зубочелюстными аномалиями, в лечении которых используются брекеты.

В качестве исходных данных используется ширина коронок зубов верхней и нижней челюсти, полученные в ходе ортодонтического диагноза. Используется только 6 зубов на верхней и нижней челюстях, остальные зубы (седьмой и восьмой) не рассматриваются при формировании моделей зубочелюстных дуг пациента.

В основе «идеальной» параметрической модели зубочелюстной системы лежит сплайн (рис. 1), который проводится через семь базовых точек, положение которых определяется из установленных соотношений между зубами на основе ортодонтических методик:

1. Метод Коркхауза. Коркхаус вывел зависимость между суммой ширин верхних резцов и длиной переднего сегмента (рис. 1, a₂) и предложил свою таблицу таких зависимостей.

2. Метод Линден и Харта определяет ширину зубной дуги в области 4-х и 6-х зубов на нижней и верхней челюсти (рис. 1, a₁ и a₄) в зависимости от суммы ширин коронок верхних резцов.

3. Метод Слабковской определяет ширину зубной дуги в области третьих зубов (рис. 1, a₃) на верхней и нижней челюсти в зависимости от суммы ширин нижних резцов.

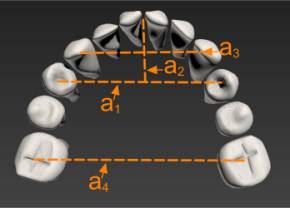
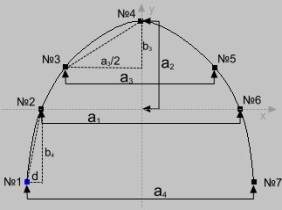
Рис. 1. Алгоритм построения сплайна для верхней и нижней зубной дуги

Алгоритм построения двух сплайнов для верхней и нижней зубной дуги идентичен, поэтому рассмотрим построение сплайна только для верхней зубной дуги.

Установим, что точки №2 и №6 лежат на оси X, а точка №4 – на оси Y. Расстояние между точками №2 и №6 равно величине между четвертыми зубами по методу Линден/Харта (a₁), расстояние от оси X до точки №4 равно величине по методу Коркхауза [1] (a₂) из таблицы «Взаимосвязи» [1] в соответствии с вычисленной суммой ширин первых четырех зубов (sum4). Таким образом, координаты точек №2, №6 и №4 будут равны соответственно (-a₁/2, 0), (a₁/2, 0) и (0, a₂).

Расстояние между точками №3 и №5 равно величине между третьими зубами по методу Слабковской (a₃) в соответствии с сумой sum4 из таблицы «Показатели ширины зубных рядов в области клыков» [2]. Для определения значений координат этих точек по оси Y расстояние между точками №4 и №3 принимаем равным сумме ширин трех резцов (sum3). Из образовавшегося прямоугольного треугольника по данным a₃/2 и sum3 вычисляем значение b_3.Таким образом, координаты точек №3 и №5 равны соответственно (-a₃/2, a₂ -b₃) и (a₃/2, a₂-b₃).

Расстояние между точками №1 и №7 (a₄), расположенными на одной прямой параллельной оси X, вычисляется по методу Линден/Харта из таблицы «Взаимосвязи» [1] в соответствии с величиной sum4. Координат этих точек по оси Y вычисляются из прямоугольного треугольника, создаваемого точками №1, №2 и точкой. В соответствии с положением зубов на зубной дуге гипотенуза этого треугольника равна сумме половины ширины четвертого и шестого зубов и ширины пятого зуба. Длина катета d вычисляется путем разницы расстояний между a₄и a₁. Таким образом, координаты точек №1 и №7 будут равны соответственно (-a₄/2, -b₄), (a₄/2, -b₄).

Через базовые точки проводится сплайн Бизье, повторяющий форму верхней дуги. Аналогичным образом находятся базовые точки для построения сплайна нижней зубной дуги.

Для построения параметрических зубных дуг используются, подготовленных ранее в файле [3], 12 моделей зубов среднестатистических размеров постоянных зубов по В.Л.Устименко [1] на верхней и нижней челюстях.

Программная обеспечение реализовано на языке MaxScript в трехмерном пакете Autodesk 3ds Max. С помощью интерфейса программы специалистом вводится ширина 12 зубов пациента в миллиметрах.

Модели зубов, подготовленные ранее, корректируются в соответствии с шириной зуба пациента. После корректировки размеров каждого зуба, в соответствии с таблицей физических размеров брекетов «McLaughlin-Bennet-Trevist 22 / Assortments» для каждого зуба задается угол наклона относительно саггитальной (локальной оси X) и окклюзионной (локальной оси Z) плоскости.

Так как используются 12 зубов для верхней и нижней челюсти, остальные 12 зубов, симметрично расположенных на зубных дугах, получаем путем дублирования и зеркального отражения по оси Z.

Далее полученные 24 зуба равномерно распределяются вдоль созданных сплайнов с помощью встроенных в язык MaxScript функций. Положение некоторых зубов автоматически корректируется в зависимости от положения семи базовых точек.

В программе предусмотрена возможность изменения параметров и положения каждого зуба.

Таким образом, используя ширину зубов пациента, с помощью разработанного алгоритма была построена «идеальная» трехмерная модель зубочелюстной системы (рис. 2), отражающая положение зубов пациента после планируемого лечения.

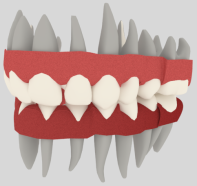
Рис. 2. Построенная трехмерная модель зубочелюстной системы

Литература

1. Антропометрические и графические методы в диагностике зубочелюстных аномалий. Учебно-методическая разработка для иностранных студентов стоматологического факультета. – Мн.: МГМИ, 1998. – 36 с.

2. Инновация в ортодонтии: учеб.-метод. Пособие для элективного курса / И 67 И.В. Токаревич [и др.]. – Минск: БГМУ, 2008. – 44с.

3. Васильева, Ю.Д. Параметрическая трехмерная модель зубочелюстной системы / Ю.Д. Васильева, // Вести Института современных знаний. 2012. – №3 (40). – С. 31 – 36