А.И. Долгарев
ГАЛИЛЕЕВЫ И ЕВКЛИДОВЫ
КРИВИЗНЫ
ЕВКЛИДОВЫХ
КРИВЫХ
Рассматриваются регулярные кривые 3-мерного евклидова пространства. Для них ранее введены галилеева кривизна и галилеево кручение; установлено, что евклидова кривая однозначно определяется галилеевыми натуральными уравнениями. Ниже изучаются свойства галилеевых кривизн евклидовой кривой, их связь евклидовыми кривизнами.
На страницах
177, 195, 199, 263 и других в [1], П.К. Рашевский пишет об изображении объектов
евклидова и псевдоевклидова пространств соответствующими объектами аффинного
пространства. Всякий объект – репер, линия, плоскость и т.д. евклидова и
псевдоевклидова пространств является объектом аффинного пространства, но как
аффинный объект, он не обладает евклидовыми и псевдоевклидовыми свойствами.
Введя в аффинное пространство скалярное произведение его векторов, мы выявляем
метрические свойства рассматриваемых объектов; аффинная геометрия метрических
свойств объектов не выявляет, хотя объект таковыми свойствами обладает. Кривая
аффинного пространства ![]() обладает и
евклидовыми и галилеевыми свойствами. Обнаружить эти свойства позволяет
соответствующее скалярное произведение векторов в линейном пространстве
обладает и
евклидовыми и галилеевыми свойствами. Обнаружить эти свойства позволяет
соответствующее скалярное произведение векторов в линейном пространстве ![]() аффинного пространства
аффинного пространства
![]() .
.
Рассматривается
аффинное пространство ![]() с действительным
линейным пространством
с действительным
линейным пространством ![]() , представляющим собой арифметическое пространство
, представляющим собой арифметическое пространство ![]() без нормы векторов,
т.е. без скалярного произведения векторов. В связи с этим можно говорить о геометрии
многообразия
без нормы векторов,
т.е. без скалярного произведения векторов. В связи с этим можно говорить о геометрии
многообразия ![]() , [2]. Считаем, что на
, [2]. Считаем, что на ![]() построена аффинная
геометрия, т.е. рассматривается пространство
построена аффинная
геометрия, т.е. рассматривается пространство ![]() с линейным пространством
с линейным пространством
![]() . На
. На ![]() определено евклидово
скалярное произведение векторов. Элементы галилеевой геометрии никак не используются,
с ними можно познакомиться в [3]. Определены галилеевы кривизна и кручение
евклидовой кривой, [4]. Основное достоинство использования галилеевых методов в
евклидовой геометрии состоит в том, что галилеевы натуральные уравнения
значительно проще описывают евклидовы кривые, чем их евклидовы натуральные
уравнения.
определено евклидово
скалярное произведение векторов. Элементы галилеевой геометрии никак не используются,
с ними можно познакомиться в [3]. Определены галилеевы кривизна и кручение
евклидовой кривой, [4]. Основное достоинство использования галилеевых методов в
евклидовой геометрии состоит в том, что галилеевы натуральные уравнения
значительно проще описывают евклидовы кривые, чем их евклидовы натуральные
уравнения.
1. Основные галилеевы понятия в евклидовой теории кривых
1.1. Евклидовы кривизны
Линия
аффинного пространства ![]() описывается в
аффинном репере
описывается в
аффинном репере ![]() векторной функцией
векторной функцией
![]() , (1)
, (1)
здесь ![]() действительные
функции действительного переменного. Определяя евклидово скалярное произведение
векторов, превращаем аффинное пространство
действительные
функции действительного переменного. Определяя евклидово скалярное произведение
векторов, превращаем аффинное пространство ![]() в евклидово
пространство
в евклидово
пространство ![]() , аффинный репер заменяем ортонормированным репером
, аффинный репер заменяем ортонормированным репером ![]() . Аффинная кривая (1) в результате становится евклидовой,
т.е. мы получаем средства для изучения евклидовых свойств аффинной линии.
Считаем линию (1) регулярной класса
. Аффинная кривая (1) в результате становится евклидовой,
т.е. мы получаем средства для изучения евклидовых свойств аффинной линии.
Считаем линию (1) регулярной класса ![]() . Покомпонентные функции
. Покомпонентные функции ![]() регулярной кривой (1)
обратимы, пусть
регулярной кривой (1)
обратимы, пусть ![]() обратная функция к
обратная функция к ![]() , в задании (1) кривой заменим параметризацию, считая
, в задании (1) кривой заменим параметризацию, считая ![]() ; получаем:
; получаем:
![]() =
= ![]() ,
,![]() . (2)
. (2)
Это выделенная параметризация евклидовой кривой. Векторы производных функции (2) таковы:
![]() =
= ![]() ,
, ![]() =
= ![]() ,
, ![]() .
.
Функции производных, начиная со второго порядка, имеют одну нулевую компоненту. Вычислительные формулы кривизны и кручения евклидовой кривой, как известно, есть
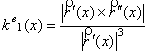 ,
, ![]() . (3)
. (3)
Евклидовы
кривизны евклидовой кривой далее обозначаем ![]() . Ниже используются галилеевы кривизны евклидовой кривой:
. Ниже используются галилеевы кривизны евклидовой кривой: ![]() .
.
Параметризация
(2) евклидовой кривой напоминает естественную параметризацию галилеевой кривой ![]() , см. [3, с. 56].
, см. [3, с. 56].
1.2. Каппа-функция евклидова вектора
Введена каппа-функция евклидова вектора в [3, с. 59 – 61].
1. ЛЕММА. Пусть ![]() евклидов вектор. Производная единичного вектора направления
евклидов вектор. Производная единичного вектора направления ![]() разлагается по векторам
разлагается по векторам ![]() следующим образом
следующим образом
![]() =
= ![]() . (4)
. (4)
Здесь ![]() скалярное
произведение векторов
скалярное
произведение векторов ![]() и
и ![]() .
.
2.
ЛЕММА. В случае двумерного вектора ![]() производная единичного вектора направления
производная единичного вектора направления ![]() равна
равна
![]() =
= ![]() , где
, где ![]() ,
, ![]() .
. ![]() . (5)
. (5)
ОПРЕДЕЛЕНИЕ 1.
Скалярный множитель ![]() разложения (5) называется
разложения (5) называется ![]() функцией
(каппа-функцией) евклидова вектора
функцией
(каппа-функцией) евклидова вектора ![]() ,
, ![]() .
.
Иначе говоря, ![]() функция вектора
функция вектора ![]() есть модуль вектора
есть модуль вектора ![]() , т.е.
, т.е.
![]() =
= ![]() .
.
1.3. Галилеевы кривизны
евклидовой кривой
По аналогии с определением галилеевой кривизны галилеевой кривой в естественной параметризации, [3, с. 58 ], вводим
ОПРЕДЕЛЕНИЕ 2.
Галилеевой кривизной евклидовой кривой (2) в выделенной параметризации ![]() =
= ![]() в ее обыкновенной точке называется величина
в ее обыкновенной точке называется величина
![]() =
= ![]() =
= ![]() ; (6)
; (6)
Вектор ![]() называется вектором
галилеевой кривизны евклидовой кривой, единичный вектор галилеевой кривизны
есть
называется вектором
галилеевой кривизны евклидовой кривой, единичный вектор галилеевой кривизны
есть
![]() =
= ![]() =
= ![]() . (7)
. (7)
По (7), ![]() . По (5) получаем вектор
. По (5) получаем вектор ![]() , считая
, считая ![]() .
.
![]() =
= ![]() ,
, ![]() =
=![]() :
: ![]() ;
; ![]() .
. ![]() . (8)
. (8)
Плоскость ![]() , см. (7), является соприкасающейся для кривой
, см. (7), является соприкасающейся для кривой ![]() . Вектор
. Вектор ![]() характеризует
отклонение кривой
характеризует
отклонение кривой ![]() от соприкасающейся
плоскости.
от соприкасающейся
плоскости.
ОПРЕДЕЛЕНИЕ
3. Галилеевым кручением евклидовой кривой
(2) в выделенной параметризации ![]() =
= ![]() называется величина
называется величина
![]() =
= ![]() =
= ![]() . (9)
. (9)
Вектор ![]() называется вектором
галилеева кручения евклидовой кривой, единичный вектор галилеева кручения
есть
называется вектором
галилеева кручения евклидовой кривой, единичный вектор галилеева кручения
есть ![]() .
.
1.4. Галилеевы натуральные уравнений евклидовой кривой
Согласно теории кривых пространства-времени Галилея, см. [5], галилеева кривая определяется функциями своих кривизн. Для евклидовых кривых в выделенной параметризации справедливо следующее утверждение.
3.
ТЕОРЕМА. Компоненты ![]() кривой (2) в выделенной
параметризации являются решением системы обыкновенных дифференциальных уравнений
кривой (2) в выделенной
параметризации являются решением системы обыкновенных дифференциальных уравнений
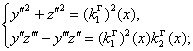 (10)
(10)
где ![]() ,
, ![]() заданные на интервале
заданные на интервале ![]() функции класса
функции класса ![]() галилеевых кривизн.
Единственная кривая (2) определяется начальными условиями
галилеевых кривизн.
Единственная кривая (2) определяется начальными условиями
![]() ,
, ![]() ,
, ![]() .
.
Обозначим:
![]() ,
, ![]() . По определениям (6) и (9) галилеевых кривизн евклидовой
кривой (2) в выделенной параметризации получаем систему обыкновенных
дифференциальных уравнений (10). Ее решением являются компоненты
. По определениям (6) и (9) галилеевых кривизн евклидовой
кривой (2) в выделенной параметризации получаем систему обыкновенных
дифференциальных уравнений (10). Ее решением являются компоненты ![]() задания кривой
задания кривой ![]() =
= ![]() . По виду первого уравнения системы (10), полагаем
. По виду первого уравнения системы (10), полагаем
![]() .
(11)
.
(11)
функции (11) удовлетворяют второму уравнению системы (10), так как:
![]() .
.
Интегрируя
функции (11) дважды по параметру ![]() , получаем компоненты
, получаем компоненты ![]() семейства кривых
семейства кривых ![]() в выделенной
параметризации. Каждая из полученных кривых
в выделенной
параметризации. Каждая из полученных кривых ![]() имеет заданные
галилеевы кривизну и кручение
имеет заданные
галилеевы кривизну и кручение ![]() ,
, ![]() . Указанные начальные условия фиксируют кривую
. Указанные начальные условия фиксируют кривую ![]() в пространстве, которая
проходит через точку
в пространстве, которая
проходит через точку ![]() и имеет в этой точке
вектор касательной
и имеет в этой точке
вектор касательной ![]() .
.
4. ТЕОРЕМА. Функции
![]() =
= ![]() ,
, ![]() =
= ![]()
являются галилеевыми натуральными уравнениями евклидовой кривой.
5. СЛЕДСТВИЕ. Если кривизна и кручение кривой (2) в выделенной параметризации постоянны: ![]()
![]() , то
, то
![]() =
= ![]() (12)
(12)
кривая ![]() является винтовой линией. Проекция кривой
является винтовой линией. Проекция кривой ![]() (12) на плоскость
(12) на плоскость ![]() есть
есть
![]() =
= ![]() .
.
Это
евклидова окружность с центром в начале координат и радиусом ![]() ,
,
![]() .
.
Плоская
кривая постоянной кривизны ![]() в выделенной
параметризации
в выделенной
параметризации ![]() является параболой y =
является параболой y = ![]() x2 + bx + c.
x2 + bx + c.
Регулярная евклидова плоская кривая в каждой своей обыкновенной точке имеет соприкасающуюся окружность и соприкасающуюся параболу, [5, с. 132; 6, с. 74 – 75]. Регулярная плоская евклидова кривая есть совокупность малых дуг окружностей и отрезков прямых, или малых дуг парабол и прямых. Парабола и окружность близки до порядка второй малости ко всякой регулярной кривой с ненулевой кривизной, [6, с. 74 – 75].
2. Свойства линий и ![]() функция вектора
функция вектора
2.1. Сопровождающий репер кривой. Плоскость галилеевых кривизн
Имеем
неортогональный но нормированный сопровождающий репер ![]() кривой (2), [2]. Как
уже отмечено в п. 1.3, плоскость
кривой (2), [2]. Как
уже отмечено в п. 1.3, плоскость ![]() =
= ![]() является соприкасающейся
для кривой (2), ее положение не зависит от параметризации кривой. Плоскость
является соприкасающейся
для кривой (2), ее положение не зависит от параметризации кривой. Плоскость ![]() указанного
сопровождающего репера определяется векторами галилеевой кривизны и галилеева
кручения линии (2), она называется
плоскостью галилеевых кривизн евклидовой линии (2). Плоскость
указанного
сопровождающего репера определяется векторами галилеевой кривизны и галилеева
кручения линии (2), она называется
плоскостью галилеевых кривизн евклидовой линии (2). Плоскость ![]() является соприкасающейся.
Репер
является соприкасающейся.
Репер ![]() называется галилеевым сопровождающим репером евклидовой
кривой.
называется галилеевым сопровождающим репером евклидовой
кривой.
6.
СВОЙСТВО. Разложение вектора ![]() по векторам
по векторам ![]() есть:
есть:
![]() . (13)
. (13)
Вектор
в числителе равенства для ![]() в (13)
в (13)
![]()
рассматривается в [7, с. 32; 8,
с. 102; 5, с. 98 - 102]. Появляется вектор в результате вычисления двойного
векторного произведения ![]() . Но нигде не упоминается и не используется вектор вида
. Но нигде не упоминается и не используется вектор вида ![]() и каппа-функция
евклидова вектора.
и каппа-функция
евклидова вектора.
7. СВОЙСТВО. Для евклидовой кривизны линии (2) выполняется равенство
![]() =
=![]() .
.
8. СВОЙСТВО. Спрямляющая плоскость линии ![]() есть
есть ![]() .
.
Отметим некоторые свойства плоскости галилеевых кривизн евклидовой линии.
9. ТЕОРЕМА. Линия (2) является плоской, если и только если ![]() . Линия (2) является прямой, если и только если
. Линия (2) является прямой, если и только если ![]() ; при этом и
; при этом и ![]() .
.
#
Вектор ![]() характеризует
отклонение кривой от соприкасающейся плоскости, п. 1.3. И
характеризует
отклонение кривой от соприкасающейся плоскости, п. 1.3. И ![]() если и только если
отклонения нет и линия лежит в соприкасающейся плоскости. Линия (2) является
прямой, если и только если
если и только если
отклонения нет и линия лежит в соприкасающейся плоскости. Линия (2) является
прямой, если и только если ![]() . #
. #
10. СВОЙСТВО. Не существует плоскости галилеевых кривизн для плоской евклидовой линии.
#
Плоская линия имеет нулевое галилеево кручение, теорема 9, а один вектор галилеевой
кривизны ![]() плоскости не
определяет. В этом случае плоскость галилеевых кривизн
плоскости не
определяет. В этом случае плоскость галилеевых кривизн ![]() вырождается в прямую
линию. #
вырождается в прямую
линию. #
11.
ТЕОРЕМА. Плоскость галилеевых кривизн
![]() евклидовой линии имеет в евклидовом пространстве неизменное
направление, она движется параллельно сама себе при движении точки
евклидовой линии имеет в евклидовом пространстве неизменное
направление, она движется параллельно сама себе при движении точки ![]() по линии.
по линии.
#
Векторы ![]() и
и ![]() разложены по базису
разложены по базису ![]() евклидовой плоскости
евклидовой плоскости ![]() , см. (7) и (8). При движении обыкновенной точки
, см. (7) и (8). При движении обыкновенной точки ![]() по линии плоскость
по линии плоскость ![]() параллельна плоскости
параллельна плоскости
![]() . #
. #
Направление
плоскости ![]() определяется вектором
ее нормали
определяется вектором
ее нормали ![]() .
.
Это
свойство плоскости галилеевых кривизн евклидовой линии ![]() аналогично свойству
нормальной плоскости галилеевой кривой
аналогично свойству
нормальной плоскости галилеевой кривой ![]() , которая является евклидовой плоскостью пространства Галилея
и потому при движении точки
, которая является евклидовой плоскостью пространства Галилея
и потому при движении точки ![]() по галилеевой кривой
евклидова плоскость движется
параллельно сама себе. Выделенную параметризацию евклидовой линии можно
получить, обращая в (2) вторую компоненту
по галилеевой кривой
евклидова плоскость движется
параллельно сама себе. Выделенную параметризацию евклидовой линии можно
получить, обращая в (2) вторую компоненту ![]() или третью компоненту
или третью компоненту
![]() . Во всех случаях имеем плоскость галилеевых кривизн евклидовой
линии. Такая плоскость у евклидовой линии одна. Она получается независимо от
того, какая функция из
. Во всех случаях имеем плоскость галилеевых кривизн евклидовой
линии. Такая плоскость у евклидовой линии одна. Она получается независимо от
того, какая функция из ![]() обращена; плоскость галилеевых
кривизн определяется с точностью до обозначений (с точностью до движения
евклидова пространства).
обращена; плоскость галилеевых
кривизн определяется с точностью до обозначений (с точностью до движения
евклидова пространства).
Можно
все регулярные кривые (2) евклидова пространства рассматривать в некотором
фиксированном репере ![]() , обращая всегда первую компоненту
, обращая всегда первую компоненту ![]() в векторном задании
линии. Можно считать, что плоскость галилеевых кривизн всех линий определяется
одной и той же нормалью
в векторном задании
линии. Можно считать, что плоскость галилеевых кривизн всех линий определяется
одной и той же нормалью ![]() . Этого можно добиться с помощью движений евклидова пространства.
. Этого можно добиться с помощью движений евклидова пространства.
Таким образом, выделенная параметризация евклидовой линии выделяет в евклидовом пространстве и плоскость галилеевых кривизн евклидовых линий. Например, в пространстве Солнечной системы существует плоскость, в которой лежат орбиты планет – плоскость Эклиптики. Ее положение определяется тремя положениями центра Солнца. В абстрактном евклидовом пространстве не существует геометрических соображений, выделяющих плоскость галилеевых кривизн евклидовых линий; такую плоскость можно получить, разве что, на основе физических свойств пространства. Но существование плоскости галилевых кривизн есть следствие геометрических свойств пространства. Дифференцируемость функций означает их обратимость и влечет выделенную параметризацию линий. Регулярность кривых евклидова пространства выявляет его неоднородность, а однородность является кажущейся. В каждой точке на поверхности Земли можно определить положение плоскости Эклиптики в любой заданный момент времени. Для этого используются три положения Солнца.
2.2. ![]() функция, евклидовы и галилеевы кривизны
функция, евклидовы и галилеевы кривизны
12.
ЛЕММА. ![]() функция вектора
функция вектора
![]() вычисляется и по формуле
вычисляется и по формуле
![]() =
= ![]() . (14)
. (14)
#
Доказываемое равенство получается в результате возведения ![]() функции вектора
функции вектора ![]() , см. определение 1, в квадрат.
, см. определение 1, в квадрат.
![]() =
= 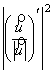 =
= 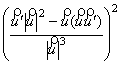 =
=  =
=
= ![]() =
= ![]() .
.
Обозначим : ![]() , тогда
, тогда ![]() . Значит
. Значит
![]() =
= ![]() .
.
Получилось значение квадрата ![]() каппа-функции
каппа-функции ![]() . Таким образом, для
. Таким образом, для ![]() выполняется (14). #
выполняется (14). #
13. ТЕОРЕМА. Каппа-функция вектора касательной ![]() связана с евклидовой кривизной линии соотношением:
связана с евклидовой кривизной линии соотношением:
![]() =
= ![]() .
.
Модуль каппа-функции вектора ![]() есть
есть
![]() =
=![]() . (15)
. (15)
# В
доказательстве свойства 6 отмечено ![]() =
=![]() . По (14) при
. По (14) при ![]() :
: ![]() =
= 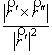 . Поэтому
. Поэтому ![]() =
= 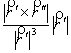 =
= ![]() . Из равенства
. Из равенства ![]() =
= ![]() следует (15). #
следует (15). #
Соединяя
формулы (14), (9) и ![]() в теореме 13, приходим ко второй формуле в (3), записанной в
виде (26) в [9, c. 57].
в теореме 13, приходим ко второй формуле в (3), записанной в
виде (26) в [9, c. 57].
14. ТЕОРЕМА. Модуль галилеева кручения евклидовой кривой (2) вычисляется также по формуле
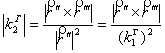 .
.
#
По равенству (13) при ![]() имеем указанную
формулу, используем (8). #
имеем указанную
формулу, используем (8). #
15.
ТЕОРЕМА. ![]() .
.
# Также, как в доказательстве леммы 12, и формулы (13) получаем доказываемое равенство. #
16.
ЛЕММА. В выделенной параметризации: ![]() .
.
# Вычисляем:
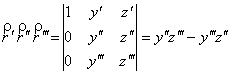 . #
. #
17.
ТЕОРЕМА. Галилеево кручение евклидовой
кривой равно
![]() . (16)
. (16)
# Формула получена по (9). #
18.
ТЕОРЕМА. Евклидовы и галилеевы кривизны
евклидовой кривой связаны соотношением
![]() . (17)
. (17)
#
Воспользуемся первой формулой в (3) вычисления кручения ![]() и добавляя в
числитель и знаменатель равные сомножители в соответствии с формулами (16), (3),
выделяем известные выражения.
и добавляя в
числитель и знаменатель равные сомножители в соответствии с формулами (16), (3),
выделяем известные выражения.
![]() =
=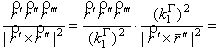 [используется (16)] =
[используется (16)] = ![]() =
=
=![]()
![]() = [используется вторая из (3)] =
= [используется вторая из (3)] = 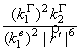 .
.
Исходная величина и конечный результат дают (17). #
Теоремы 15 и 18 связывают между собою евклидовы и галилееы кривизны евклидовой линии. В формулах кроме кривизн линии содержатся и другие величины. Первая из этих теорем связывает евклидову кривизну и галилееву кривизну. Наличие такой связи естественно ввиду существования линий без кручения, т.е. плоских линий. Линия не обладает плоскостью евклидовых кривизн, но обладает плоскостью галилеевых кривизн и она является инвариантом линии: при движении точки по линии направление плоскости галилеевых кривизн не изменяется.
19. СЛЕДСТВИЕ. Знаки евклидова и галилеева кручения евклидовой линии совпадают.
# Такой результат дает формула (17). #
Другими
словами, евклидовы кривизны есть инварианты евклидовой линии и галилеевы
кривизны есть инварианты евклидовой линии. Имеется ввиду линия в многообразии ![]() , она обладает различными наборами инвариантов. Нет оснований
признавать одни наборы определяющих инвариантов и не признавать другие.
, она обладает различными наборами инвариантов. Нет оснований
признавать одни наборы определяющих инвариантов и не признавать другие.
Отметим еще один результат.
20.
СВОЙСТВО. Модули каппа-функций первой и
второй производных функции ![]() таковы:
таковы:
![]() =
=![]() ,
, ![]() =
= ![]() =
= ![]() .
.
#
Первая из формул есть (15). По (15), ![]() , по (7),
, по (7), ![]() ,
, ![]() , и по определению 2,
, и по определению 2, ![]() . Воспользовавшись теоремой 13, находим вторую формулу. #
. Воспользовавшись теоремой 13, находим вторую формулу. #
2.3. Движение плоскости
галилеевых кривизн евклидовой линии
Главное
свойство плоскости галилеевых кривизн ![]() состоит в том, что
придвижении точки
состоит в том, что
придвижении точки ![]() по евклидовой кривой
плоскость
по евклидовой кривой
плоскость ![]() движется параллельно
сама себе, теорема 11. [10], п.4.
движется параллельно
сама себе, теорема 11. [10], п.4.
При
движении точки ![]() по линии
по линии ![]() плоскость галилеевых
кривизн
плоскость галилеевых
кривизн ![]() не может
не может
двигаться, скользя сама по себе,
так как в этом случае она перестает существовать, свойство 10. Плоскость ![]() существует, если она
занимает различные положения в евклидовом пространстве. (Имеется некоторый аналог
с элементами квантовой теории. Например, существует масса покоя электрона,
движущийся электрон есть волна.) Справедлива
существует, если она
занимает различные положения в евклидовом пространстве. (Имеется некоторый аналог
с элементами квантовой теории. Например, существует масса покоя электрона,
движущийся электрон есть волна.) Справедлива
21.ТЕОРЕМА.
Перемещение плоскости галилеевых кривизн
![]() евклидовой кривой происходит под воздействием вектора
евклидовой кривой происходит под воздействием вектора
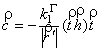 ,
,
который является ненулевой проекцией вектора ![]() на вектор
на вектор ![]() .
.
#
В (13) вектор ![]() разложен по векторам
разложен по векторам ![]() и
и ![]() . Под воздействием составляющей, коллинеарной вектору
. Под воздействием составляющей, коллинеарной вектору ![]() плоскость
плоскость ![]() скользит сама по
себе, а под воздействием составляющей
скользит сама по
себе, а под воздействием составляющей 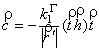 , коллинеарной вектору
, коллинеарной вектору ![]() , плоскость
, плоскость ![]() изменяет свое положение,
перемещаясь параллельно сама себе, теорема 11. Согласно свойству 10,
изменяет свое положение,
перемещаясь параллельно сама себе, теорема 11. Согласно свойству 10, ![]() . # Величина
. # Величина ![]() характеризует
скорость изменения положения плоскости галилеевых кривизн
характеризует
скорость изменения положения плоскости галилеевых кривизн ![]() евклидовой кривой.
евклидовой кривой.
22.
ТЕОРЕМА. Скорость вращения плоскости
галилеевых кривизн ![]() равна
равна ![]() .
.
# Двигаясь,
плоскость ![]() может вращаться
вокруг своих нормалей, других осей вращения плоскость
может вращаться
вокруг своих нормалей, других осей вращения плоскость ![]() не имеет. Согласно
положениям механики, вектор вращения плоскости
не имеет. Согласно
положениям механики, вектор вращения плоскости ![]() есть
есть ![]() , вектор угловой скорости коллинеарен вектору
, вектор угловой скорости коллинеарен вектору ![]() , величина скорости вращения равна
, величина скорости вращения равна
![]() =
= ![]()
![]() =
=![]() =
=![]() ,
,
см. (6) и (14) и далее (8). #
В работе [10] установлено, что евклидово пространство, содержащее регулярные кривые, неоднородно. Оно отличается от евклидова пространства, изучаемого в элементарной геометрии, [10].
Литература
- Рашевский П.К. Риманова геометрия и тензорный анализ. - М.: Наука, 1967. -664с.
2. Долгарев А.И. О геометрии 3-мерного действительного многообразия. – Вестник Татарского государственного гуманитарно-педагогического университета. – Казань, 2011, вып. 1(23). – С. 2 – 15.
- Долгарев А.И. Классические методы в дифференциальной геометрии одулярных пространств. Монография. – Пенза: ИИЦ ПГУ, 2005.- 306с.
4. Долгарев А.И. Натуральные уравнения кривых 3-мерных одулярных галилеевых пространств// Дифференциальная геометрия многообразий фигур. Межвуз. тем. сб. научн. тр. Вып. 36. – Калининград: КГУ, 2005. – С. 31 – 36.
- Выгодский М.Я. Дифференциальная геометрия. – М. – Л.: Гостехиздат, 1949. – 512 с.
- Фиников С.П. Курс дифференциальной геометрии. Изд. 2. – М.: КомКнига, 2006. – 344с.
7. Позняк Э.Г., Шикин Е.В. Дифференциальная геометрия. – М.: Изд-во МГУ, 1990. – 384с.
- Рашевский П.К. Курс дифференциальной геометрии. – М.: Гостехиздат, 1956. 420с.
9. Дубровин Б.А, Новиков С.П., Фоменко А.Т. Современная геометрия. //М.: Наука – 1979, 760с.
- Долгарев А.И. Различные по Ф. Клену евклидовы геометрии: элементарная и диф-
ференциальная.// Materialy IX Miedzynarodowej naukowi-praktycznej konferencji
“Strategiczne pytania swiatowej nauki – 2013” Volume 28. Matematyka. Fizyka.
Nowoczesneinformacyjne technologie.: Przemysl. Nauka i studia – 96 str. C. 3 – 8.