Кобзєв М.С.

ІПСА, Національний технічний університет України «КПІ»

Самоорганізовна інкрементна нейронна мережа

Інкрементна нейронна мережа являє собою двохшарову нейронну структуру. Перший шар використовується для генерації топологічної структури вхідного сигналу. Отримуються деякі вузли для представлення густини імовірності вхідного сигналу, коли закінчено навчання першого шару. Для другого шару, використовуються вузли, ідентифіковані у першому шарі, як вхідні данні.

Однаковий алгоритм використовується для навчання як першого так і другого шару. У другому шарі використовується постійний поріг подібності замість адаптивного порогу, використовуваного в першому шарі.

Умовні позначення, використані у описі алгоритму:

A Набір вузлів, використовується для зберігання вузлів.

N(A) Число вузлів в А.

C Множина ребер

N(C) Число ребер в C.

W_i N-вимірний ваговий вектор вузла і.

E_i Накопичена помилка вузла i

M_i Накопичена кількість сигналів з вузла і

R_i Успадковані радіус помилки вузла і

C_i мітка кластеру

Q число кластерів

T_i Поріг подібності

N_i Множина безпосередніх топологічних сусідів вузла і

L_i Кількість безпосередніх топологічних сусідів вузла і

age(i,j) Вік ребра, який з’єдную вузол i та вузол j

Алгоритм:

1. Ініціалізувати множину А двома вузлами, с1 та с2

A = {c₁, c₂},

з ваговими векторами, обраними випадково з начальної вибірки.

Ініціалізувати C, C A х A, пустою множиною

2. Ввести новий сигнал ξ є R_n

3. Провести пошук по А для визначення переможця та другого місця

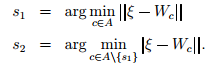
Якщо відповідні відстані між ξ та s₁ або s₂ більше, ніж пороги подібності Т_s1 або T_s2, то вхідний сигнал – новий вузол. У такому випадку потрібно додати його до А та піти на крок (2)

4. Якщо ребро між s1 та s2 не існує, то створити його та додати до С

Виставити вік ребра у нуль

age _{(s1, s2)} = 0

5. Збільшити вік усіх вихідних ребер із s1

6. Додати Евклідову відстань між вхідним сигналом та переможцем до накопичувальної похибки

7. Додати 1 до накопичувального числа сигналів

8. Адаптувати вагові вектори переможця та його безпосередніх топологічних сусідів по часткам є1(t) та є2(t) від загальної відстані до вхідного сигналу

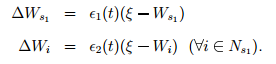
є1(t) – швидкість навчання переможця, а є2(t) – швидкість навчання сусіда

9. Видалити ребра з віком, що перевищує поріг

10. Якщо кількість вхідних сигналів сгенерованих до цих пір, є цілим кратним λ, вставити новий вузол та видалити вузли наступним чином:

- Визначити вузол q з максимальною накопиченою помилкою Е

- Визначити, серед сусідів q, вузол f з максимальною накопиченою помилкою

- Додати новий вузол r до мережі та інтерполювати його ваговий вектор з q та f:

- Інтерполювати акумульовану помилку Е_r, акумульоване число сигналів M_r та успадкований радіус помилки R_r:

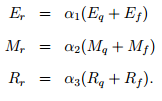
- Зменшити акумульовану кількість сигналів q та f за часткою

- Вирішити, чи була вставка успішною. Якщо радіус помилки більший за успадкований R_i

іншими словами, якщо вставка не може зменшити середню помилку цієї локальної області, то вставка не була успішною. Тоді r видаляємо з А, інакше

- Якщо вставка була успішною, вставляємо ребра, з’єднуючі новий вузол r з вузлами q та f, та видаляємо ребро між ними

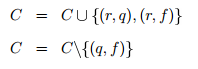
- Для всіх вершин в А, шукаємо вузли, які мають одного сусіда, потім порівнюємо акумульовану кількість сигналів цих вузлів з середньою кількістю по всіх вершинах. Якщо вершина має тільки одного сусіда, та акумульована кількість сигналів менша, ніж поріг адаптації, видаляємо її з множини А:

1 > c > 0.

Якщо існує багато шумів в вихідній вибірці, с повинно бути більшим.

11. Після довгого, постійного за часом періоду, повідомити кількість кластерів, вивести вершини, що належать різним класам:

- Ініціалізувати всі вузли, як некласифіковані

- Цикл: випадково вибрати некласифіковану вершину і з А, помітити її як класифіковану та помітити її як клас С_і

- Пройти А, знайти всі некласифіковані вершини, приєднані до і якимось шляхом. Помітити вершини, як класифіковані та додати до С_і

- Якщо існують некласифіковані вузли, продовжити з метки «Цикл»

Для першого шару немає попередніх даних про вхідні данні, тому використовується схема, за якою поріг подібності адаптується до вибірки. Для кожного вузла поріг адаптується незалежно. Спочатку вважається, що всі данні належать одному кластеру, поріг прямує до нескінченності. Після періоду навчання, вхідний потік ділиться на різні малі групи, кожна з яких включає вузол та його безпосередніх сусідів. Деякі з цих груп можуть бути об’єднані у більшу, котрі відділені одне від одного. Назвемо їх кластерами. Поріг подібності повинен бути більшим, ніж внутрішньо-кластерні відстані та менший, ніж між-кластерні. Ґрунтуючись на цій ідеї, поріг подібності розраховується за наступним алгоритмом [1]:

1. Ініціалізувати поріг і-го вузла нескінченністю, коли його щойно додали до множини вузлів

2. Коли і є переможцем або другим місцем, оновити поріг подібності наступним чином:

- Якщо вузол має безпосередніх топологічних сусідів, то Ті стає рівним максимальній відстані між і та його сусідами

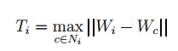
- Якщо вузол і не має сусідів, то Ті стає рівним мінімальній відстані до всіх інших вузлів з А

Для другого шару, вхідний потік складається з результатів першого шару. Після навчання на першому шарі, отримуємо грубі результати та топологічну структуру. Використовуючи ці знання, вираховуємо внутрішньо-кластерну відстань, як

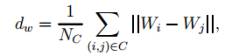
та обчислюємо між-кластерну відстань, як

Таким чином, під внутрішньо-кластерна відстань мається на увазі середня довжина усіх ребер, а між-кластерна – мінімальну довжину між двома кластерами. Постійний поріг подібності повинен бути між цими числами [2].

Поріг має бути більшим за внутрішньо-кластерну відстань, та менший за між-кластерну. Під впливом перекриття або шуму, деякі між-кластерні відстані виявляються меншими за внутрішньо-кластерні, тому для пошуку порогу подібності для другого шару використовується наступний алгоритм[3]:

1. Встановити Т_с

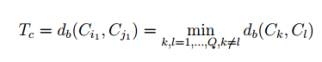
2. Якщо Т_с менше за внутрішньо-кластерну відстань, то встановити Т_с в наступну мінімальну внутрішньо-кластерну відстань.

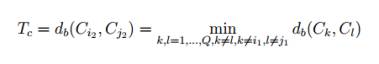
3. Виконувати (2), доки Т_с більше за поріг подібності.

Швидкість навчання можна задати наступним чином, по аналогією з мережою «нейронний газ»[4]:

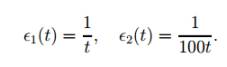
Тут параметр t являє собою кількість вхідних сигналів, для яких цей конкретний вузол був переможцем. Цей алгоритм відомий як метод k-середніх. Вузол завжди є середнім арифметичним вхідних сигналів, для яких він був переможцем.

Коли вставка між вузлом q та f відбулась, встає задача зменшення акумульованих значень похибки та кількості сигналів, а також аналогічна: як призначити ці значення до нового вузла.

У роботі професора Шена[1] пропонується обгрунтування наступних параметрів для навчання мережі з найменшими втратами:

У даній статті було покроково розглянуто алгоритм самоорганізовної інкрементної нейронної мережі, з обґрунтуванням використаних у ньому параметрів.

Література:

1. An enhanced self-organizing incremental neural network for online unsupervised learning (Electronic recourse) / Shen F., Ogura T., Hasegawa O. // Neural Networks. – 2007. – Vol.20, pp.893-903. – Mode of access: http://www.sciencedirect.com/science/article/pii/S0893608007001190

2. Arbib M.A. Handbook of brain theory and neural networks./ Arbib M.A., – 2nd edition. – Cambridge: MIT, 2003. – 1290 p.

3. Хайкин C. Нейронные сети: полный курс, 2-е издание./ Хайкин C., – М.: Издательский дом «Вильямс», 2008. – 1104 с.

4. Training multi-layered neural network [Electronic recourse] / Fukushima K. // Neural Networks. – 2013. – Vol.40, pp.18-31. – Mode of access: http://www.sciencedirect.com/science/article/pii/S0893608013000051