Педагогічні науки / 5. Сучасні методи викладання

К.п.н. Ачкан В.В., Василенко А.С.

Бердянський державний педагогічний університет

Система компетентнісно орієнтованого тестового контролю в процесі вивчення теми тригонометричні рівняння та нерівності у курсі математики у ВНЗ I-II рівнів акредитації

Нове освітнє середовище передбачає й новий зміст освіти, нові технології навчання і виховання, розвиток інтелектуальних здібностей студентів. Сьогодні вищі навчальні заклади мають готувати не лише носія знань, а й творчу особистість, яка здатна використовувати здобуті знання для конкурентоспроможної діяльності у будь-якій сфері суспільного життя, тобто формувати компетентну особистість. Нові запити сучасного суспільства щодо результативності освітніх систем спричинюють рух до формування змісту освіти на компетентнісній основі, що, відповідно, обумовлює потребу розробки технології оцінювання рівня сформованості компетентностей.

Математична освіта покликана зробити вагомий внесок у формування компетентостей як загальних цінностей, що базуються на знаннях, досвіді, здібностях, які було набуто завдяки навчанню.

Питанням впровадження компетентнісного підходу в математичну освіту присвячені роботи І. Аллагулової [2], С. Ракова [7], Н. Ходирєвої, О. Шавальової та ін. Зазначений цикл досліджень охоплює питання, пов’язані із визначенням основних математичних компетентностей та напрямів їх набуття, формуванням математичних компетентностей учителя математики на основі дослідницького підходу з використанням інформаційних технологій; підготовкою майбутніх учителів до формування математичних компетентностей учнів; реалізацією компетентнісного підходу в процесі математичної підготовки студентів медичних коледжів.

Останні результати досліджень науковців (В. Аванесов [1], А. Анастазі, В. Беспалько, І. Булах [3], А. Майоров, М. Челишкова, та ін.), котрі приділяли увагу проблемі контролю, взагалі, і тестовому контролю, зокрема, доводять, що, незважаючи на наявні результати завершених досліджень, технологія проведення тестового контролю залишається недостатньо розробленою в плані обґрунтування її психолого-педагогічних основ та здатності перевіряти рівень сформованості компетентностей.

Рівень сформованості компетентностей вимірюється через рівень навчальних досягнень, процедура оцінювання яких переноситься, здебільшого, на останнє чи передостаннє заняття вже вивченої теми в результаті якого створюється загальна картина засвоєння студентами навчального матеріалу, але втрачається можливість оцінити розвиток у студентів інтелектуальних і спеціальних умінь та навичок. Отже, оцінюється насамперед рівень знань і ступінь розвиненості пам’яті у студентів, а інтелектуальний розвиток залишається поза увагою вчителя. Щоб уникнути подібної ситуації, слід, перш за все, відійти від орієнтації навчання на знання як основний показник навчальних досягнень учнів і запровадити компетентнісно орієнтований підхід.

Компетентнісно орієнтований підхід передбачає більш чітке визначення кола інтелектуальних і спеціальних умінь та, відповідно, розробку системи завдань, спрямованих на їх розвиток. Такі завдання можна використовувати під час навчання, поточного та підсумкового контролю, їх самостійне використовування дозволить визначити і оцінити рівень сформованості компетентностей студентів.

Як зазначав С. Раков [7], рівень складності навчальних задач можна інтерпретувати через рівні засвоєння понять: концептуалізація поняття – засвоєння концептуальних ідей, що лежать в основі поняття, наприклад, типових ситуацій, у яких його доцільно використовувати; властивості поняття – засвоєння основних властивостей поняття; застосування поняття – уміння «бачити» та застосовувати поняття на практиці; систематизація поняття – узагальнення, зв’язок з іншими поняттями, межі поняття. Тести, які відповідають вищезазначеній класифікації рівнів навчальних досягнень учнів прийнято називати компетентнісними тестами.

У даній публікації ми зосередили свою увагу на курсі математики у ВНЗ І-ІІ рівнів акредитації. Мета навчання математики у вищих навчальних закладах І-ІІ рівнів акредитації полягає у забезпеченні рівня підготовки студентів з математики, необхідного для спеціальної підготовки та майбутньої професійної діяльності [5].

Змістове наповнення програми реалізує компетентнісний підхід до навчання, спрямований на формування системи відповідних знань, навичок, досвіду, здібностей і ставлення (відношення), яке дає змогу обґрунтовано стверджувати про застосування математики в реальному житті.

Виділяють три рівня математичної компетентності: рівень відтворення, рівень встановлення зв’язків та рівень міркувань [4].

Перший рівень (рівень відтворення) – це пряме застосування в знайомій ситуації відомих фактів, стандартних прийомів, розпізнавання математичних об'єктів і властивостей, виконання стандартних процедур, застосування відомих алгоритмів і технічних навичок, робота зі стандартними, знайомими виразами і формулами, безпосереднє виконання обчислень.

Другий рівень (рівень встановлення зв'язків) будується на репродуктивній діяльності з розв'язування задач, які, хоча і не є типовими, але все ж знайомі учням або виходять за рамки відомого лише в незначній мірі. Зміст завдання підказує, матеріал якого розділу математики треба використовувати і які відомі методи застосувати. Зазвичай у цих завданнях присутні більше вимог до інтерпретації розв’язку, вони передбачають встановлення зв'язків між різними уявленнями ситуації, що описана в задачі, або встановлення зв'язків між даними в умові задачі.

Третій рівень (рівень міркувань) будується як розвиток попереднього рівня. Для розв'язування задач цього рівня потрібні певна інтуїція, роздуми і творчість у виборі математичного інструментарію, інтегрування знань з різних розділів курсу математики, самостійна розробка алгоритму дій. Завдання, як правило, включають більше даних, від студентів часто вимагається знайти закономірність, провести узагальнення і пояснити або обґрунтувати отримані результати.

У процесі проведення тестового контролю з математики послідовно реалізується перевірка усіх трьох рівнів математичної компетентності студентів.

У ході дослідження розроблено систему тестового контролю в курсі математики в процесі вивчення теми “тригонометричні рівняння та нерівності” у ВНЗ I-II рівня акредитації в умовах реалізації компетентісного підходу до навчання.

Завдання з вибором однієї правильної відповіді, як в тестах для поточного, так і в тестах для тематичного та підсумкового контролю передбачають перевірку процедурної компетентності студентів тобто перевірки володіння ними типовими методами розв’язування задач. Завдання, в яких передбачено скласти відповідності, записати коротко правильну відповідь, побудувати математичну модель, виявляють перш за все сформованість логічної та конструктивно-графічної компетентностей в студентів, тобто студент при розв’язуванні таких задач повинен виявити здатність використовувати як типові методи розв’язування, так і здатність будувати моделі практичних ситуацій, використовуючи графічні або аналітичні методи. А от завдання, які передбачають розв’язання задач з розгорнутою обґрунтованою відповіддю, виявлять сформованість дослідницької та конструктивно-графічної компетентностей, спираючись на сформовані процедурну та логічну компетентності.

Наведемо компетентнісний тест для поточного контролю з теми “тригонометричні рівняння та нерівності”:

Завдання 1-4 (рівень відтворення) мають чотири варіанта відповіді, серед яких лише один правильний. Ці завдання відповідають рівню відтворення, тобто учень повинен вміти використовувати стандартні прийоми, розпізнавати математичні об’єкти і властивості, виконувати стандартні процедури.

Виберіть правильну, на ваш погляд, відповідь та виділіть її.

1. На якому одиничному колі зображено розв’язок нерівності ?

2. На якому одиничному колі зображено розв’язок нерівності

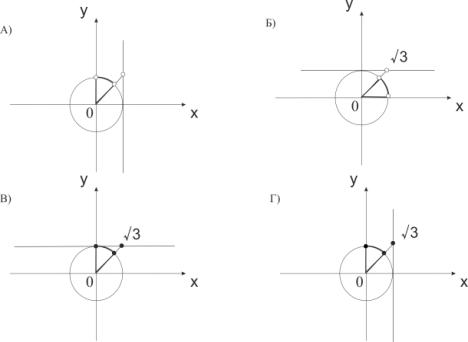
3. Розв’яжіть рівняння

4. Розв’яжіть рівняння

5. Скільки коренів має рівняння ?

а) Один; б) не має коренів; в) безліч; г) два.

Шосте та сьоме завдання відповідають рівню встановленню зв’язків, тобто спираються на репродуктивну діяльність з розв’язування завдань, які, хоча і не є типовими, але все ж знайомі учням або несуттєво виходять за рамки відомого.

Розв’яжіть завдання шість та сім і впишіть відповідь в бланк відповідей.

6. Розв’яжіть рівняння

7. Розв’яжіть нерівність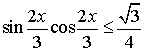

Восьме та дев’яте завдання відповідають рівню міркувань і створюються як розвиток попереднього рівня. Для розв’язування завдань цього рівня потрібні певна інтуїція, роздуми і творчість у виборі математичного інструментарію.

Розв’язання восьмого та дев’ятого завдань повинне містити повне пояснення, записане у вигляді послідовних логічних дій, із посиланням на математичні факти, з яких випливає те чи інше твердження.

8. Розв’яжіть рівняння

9. Знайдіть область визначення функції

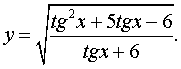
Використання запропонованих елементів системи тестового контролю дозволяє виявити рівень сформованості математичних компетентностей студентів у процесі вивченні математики у ВНЗ I-II рівнів акредитації, створити систему корегуючи вправ, корегувати зміст, форми та методи навчання та, як наслідок, підвищити показники успішності навчання та мотивації до вивчення математики.

Література:

1. Аванесов B.C. Композиция тестовых заданий / В.С. Аванесов. – М. : Центр тестирования, 2002. – 240 с.

2. Аллагулова И.Н. Формирование математической компетентности старшеклассника в образовательном процессе: дис. … канд. пед. наук: 13.00.01 / Аллагулова Ирина Николаевна. – Оренбург, 2007. – 190 с.

3. Булах І.Є. Створюємо якісний тест: навч. посіб. / І.Є. Булах, М.Р. Мруга. – К. : Майстер-клас, 2006 – 160 с.

4. Казачек Н.А. Математическая компетентность будущего учителя математики / Н.А. Казачек. – [Електронний ресурс]. – Режим доступу: ftp://194.226.213.129/text/kazachek_121_106_110.pdf

5. Математика. Навчальна програма для вищих навчальних закладів І-ІІ рівнів акредитації, які здійснюють підготовку молодших спеціалістів на основі базової загальної середньої освіти. – [Електронний ресурс]. – Режим доступу: http://vzvo.gov.ua/navchalni-prohramy/91-mathematics-for-university-i-ii-ra.html

6. Пометун О.І. Компетентнісний підхід до оцінювання рівнів досягнень учнів / О.І. Пометун. ¾ К. : 2004. – 180 с.

7. Раков С.А. Математична освіта: компетентнісний підхід з використанням ІКТ: Монографія / С.А. Раков. – Х.: Факт, 2005. – 360 с.