Самарский
государственный технический университет, Россия
Расчет коэффициента сопротивления при движении нано- и микрочастиц в разреженном газе
Определение силы
сопротивления среды в различных условиях составляет одну из основных задач при
расчете скорости движения частиц. В общем случае движения с малыми числами
Рейнольдса сила сопротивления пропорциональна скорости движения частицы
![]()
Для упрощения будем
считать, что частица имеет сферическую форму. Как известно, для нее справедлива
формула Стокса, хотя имеются ограничения в применении этой формулы для очень
малых частиц.
![]() (1)
(1)
При выводе этой формулы
предполагалось, что у поверхности частицы нет скачка скорости, т. е. толщина
пограничного слоя (слоя, в котором происходят изменения скорости) у поверхности
частицы много больше длины свободного пробега молекул среды.
Благодаря проскальзыванию
сопротивление движению малой сферической частицы должно уменьшаться. Поправки к
формуле Стокса для малых частиц были вычислены Каннингемом, Милликеном и
Дэвисом, и формула приобрела вид:
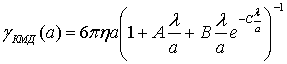
где λ — длина свободного пробега молекул, а входящие сюда
константы равны А =
1.257, В = 0.45, С = 1.1. Корреляция
Каннингема-Милликена-Дэвиса (КМД) является экспериментальной и существенно
исправляет формулу (1), расхождение появляется лишь в области больших и очень
малых радиусов [1].
С другой стороны,
величину γ(а) можно рассчитать
исходя из представления о диффузии
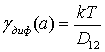
где D12 -
коэффициент взаимной диффузии для наночастиц и молекул газа. Найти коэффициент
взаимной диффузии можно используя понятие подвижности и известное соотношение
Эйнштейна
![]()
Подвижность заряженных
частиц, согласно строгой теории Ланжевена [2], задается формулой
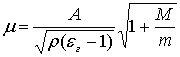
где ρ – плотность газа, εг
– относительная диэлектрическая проницаемость газа, М – масса молекулы газа, m – масса заряженной частицы. Величина А – функция параметра Λ,
определяемого выражением
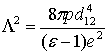
где р — давление газа,
а d12— сумма радиуса частицы и радиуса молекулы.
Коэффициент взаимной диффузии для наночастиц и молекул газа в этой модели равен
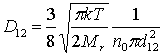
где Мr –
приведенная масса молекулы и частицы, n0 – концентрация газа, Т – температура. Коэффициент
сопротивления в этом случае можно рассчитать по формуле
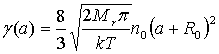 (2)
(2)
где R0 – радиус
молекулы.
Графики зависимости
коэффициента сопротивления среды (газ с молярной массой 0,1 кг/моль - тетрафторэтилен)
от размера частицы при температуре
300 К и давлении 80 Па приведены на рис.1
Различие коэффициентов сопротивления,
рассчитанных из КМД корреляции и формуле γдиф(а),
не превышает 1% в интервале размеров частиц от 40 нм до 1 мкм. Для частиц,
радиус которых меньше 40 нм, формула Каннингема-Милликена-Дэвиса дает
завышенные значения, что отмечено некоторыми авторами [например 3], поэтому более правильно
пользоваться выводами строгой теории Ланжевена. Вслед за авторами [3], хочется
отметить, что зависимость γ(а) для
наночастиц существенно отличается от
предсказываемой КМД корреляцией, инструментально закладываемой практически во
все методы измерения коэффициента диффузии аэрозолей.
Для расчета коэффициента диффузии частицы
в газе наиболее часто используется формула Эпштейна
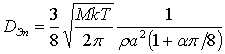 (3)
(3)
где ρ –
плотность газа, М – масса молекулы
газа, а – радиус частицы, α - коэффициент аккомодации (для
модели упругих шаров α = 0).
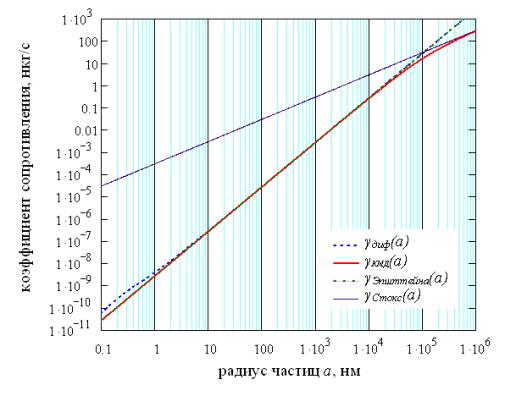
Рис. 1. Зависимости коэффициента
сопротивления движению от радиуса частицы
для тетрафторэтилена при температуре
300 К и давлении 80 Па
На графике 1. кривая для
коэффициента сопротивления, рассчитанная с применением формулы (3), изображена
зеленой штрихпунктирной линией. Характерно, что в области малых частиц (порядка
1÷10 размеров атома газа) кривая Эпштейна совпадает с кривой КМД
корреляции, а в области крупных частиц – с кривой Ланжевена. Нетрудно заметить,
что формула для коэффициента диффузии по Ланжевену (2) переходит в формулу
Эпштейна (3), если пренебречь радиусом молекулы по сравнению с радиусом частицы
и приведенную массу считать равной массе молекулы.
Таким образом, можно сделать
вывод, что для описания движения наночастиц и, в особенности, ионов в газовой
среде более справедливы формулы строгой
теории Ланжевена.
Литература:
2.
Мак-Даниель И. Процессы столкновений в ионизованных газах. М.: Мир.1967. 832с.
1.
Рудяк В. Я., Краснолуцкий С. Л. Диффузия наночастиц в разреженном газе // Журн.
техн. физики. 2002. Т. 72, вып. 7. С. 13-20.
3.
Рудяк В.Я., Дубцов С.Н., Бакланов А.М. О зависимости коэффициента диффузии
наночастиц от температуры // Письма в ЖТФ, 2008, 34(12), 48–54