Гусейнов Т.T.

Aзербайджанский архитектурно-строительный университет

МАТЕМАТИЧЕСКАЯ МОДЕЛЬ ТРУБЧАТОГО РЕЗОНАТОРА ВИБРАЦИОННОГО ПЛОТНОМЕРА ЖИДКОСТИ РАБОТАЮЩЕГО В РЕЖИМЕ СВОБОДНЫХ КОЛЕБАНИЙ

Для измерения плотности жидких сред наряду с другими плотномерами находят применение и вибрационные [ 1 ]. В общем случае эти приборы состоят из чувствительного элемента, выполненного в виде закрепленной на концах трубки, по которой организован поток исследуемой среды и системы возбуждения. последняя, как правило, состоит из электромагнитных возбудителя и приемника колебаний, а также электронного усилителя. В зависимости от реализуемого режима колебаний между усилителем и приемником колебаний отсутствует или присутствует положительная обратная связь. В первом случае имеет место режим вынужденных колебаний. Здесь плотность измеряемой среды определяется по величине амплитуды колебаний трубки. Второй случай соответствует режиму автоколебаний . В данном случае о плотности судят по частоте автоколебаний трубки, величина которой близка к ее собственным колебаниям. В то же время, в работе [ 2 ] указывается на возможность использования в вибрационных плотномерах режима свободных колебаний. Как показал проведенный анализ известных на сегодняшний день литературных источников, содержащих информацию о вибрационных измерителях плотности, в них отсутствуют какие-либо сведения о теории работы плотномеров, использующих режим свободных колебаний. С целью устранения данного пробела в настоящей работе разрабатывается и исследуется математическая модель вибрационного плотномера жидкости работающего в режиме свободных колебаний.

Дифференциальное уравнение малых колебаний трубчатого резонатора с жидкостью при рассмотрении последнего в виде системы с сосредоточенными параметрами имеет вид

(1)

где - отклонение оси резонатора от положения равновесия; - масса резонатора с жидкостью; - масса пустого резонатора; - масса жидкости в резонаторе; - плотность жидкости; - внутренний объем резонатора; - коэффициент затухания системы; - коэффициент упругости системы.

Представим (1) в следующем удобном для анализа виде

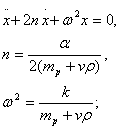(2)

где - декремент затухания; - собственная частота колебаний. Из (2) следует, что контролируемая плотность может быть определена из следующего соотношения:

(3)

где - декремент затухания пустого резонатора.

Запишем (3) в следующем удобном для последующих расчетов виде:

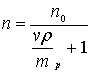(4)

Из (4) определим выражение чувствительности как

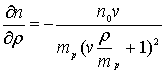(5)

Взяв частные дифференциалы от (3) по , и , перейдя к конечным приращениям, получим выражения абсолютных погрешностей соответственно от изменения внутреннего объема резонатор, плотности измеряемой жидкости и декремента затухания пустого резонатора

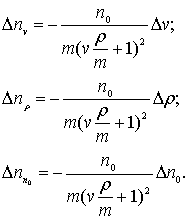(6)

Выражения (6) могут быть использованы для приближенной оценки влияния параметров резонатора на характеристики плотномера. В частности, отсюда следует, что точность измерения тем выше, чем меньше декремент затухания резонатора, т.е. чем больше его добротность.

Литература

1. Гаузнер С.И. Измерение массы, объема и плотности : учебное пособие/ С.И.Гаузнер, С.С.Кивилис, А.П.Осокина, А.Н.Павловский .- М: Изд-во стандартов , 1972 г., С.613

2. Жуков Ю.П. Вибрационные плотномеры.- М: Энергоатомиздат, 1991 г.