Determination of the concentration of the hydrodynamic-active admixture during the joint operation of the

pump and pipeline

F.A.Amirov, S.A.Agammedova

(Azerbaijan State Oil Academy)

Regulation of the operation regime of the hydraulic system through the hydrodynamic active admixtures- one of the famous methods of the reduction of the power losses (1-3). In case of use of the hydrodynamic active admixtures on the purpose of the reduction of the hydraulic drop, in term, when the parameters of the pump are determined, there is the task on the selection of the volume of the admixture through the way that provides the joint operation of the pump and pipeline.

Lets examine the task, on conditioned that the liquid is Newtonian. Dependence on the kinematic viscosity from the concentration of the hydrodynamic active admixtures may be submitted on the following order:

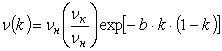(1)

there is

;

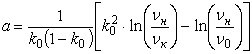There is k – volume concentration of the hydrodynamic active admixtures; n_н, n_к –kinematic viscosity of the Newtonian liquid and the additive on some temperature T; n₀ –viscosity of the liquid under the temperature T₀ and concentration of the additive к₀.

Lets include the following designation:

®

when the dependence (1) acquires the type:

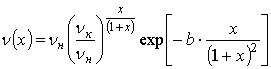(2)

there is

;

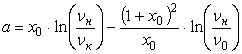Density of the solution regards with the density of the Newtonian liquid on the formula:

(3)

Volumetric flow rate equals:

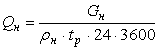(4)

there is t_p-quantity of the annual operation days of the pump device.

Index of the regime of the motion of the liquid will be the index of Reynolds:

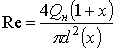(5)

Hydraulic gradient shall be determined on the formulas:

if Re(x) £ 2300 (6)

if

230aRe(х) £ 10⁵ (7)

there is -translocation quotient

Let’s determine the loss of the complete hydraulic drop on the formula:

h (x) = i × L (8)

there is i- hydraulic gradient, selecting on the formula (6) and (7) on dependence from the regime of the liquid flow; L-length of the pipeline.

For the determination of the necessary volume of the hydrodynamic active admixture it is necessary to use the balance equation of the pump hydraulic drop on the pipeline during the stated characteristic.

It shall be stated on the following form for the equation of the hydraulic characteristic during the operation of the solution with hydrodynamic active admixtures:

H_k0 = h (x) + DZ + H_k (9)

there is h (x) is the loss of the hydraulic drop; DZ-variety of the elevation mark.

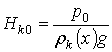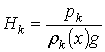; -hydraulic drop at the beginning and end of the pipeline; p₀, p_{к -} hydraulic drop at the beginning and end of the pipeline.

Characteristics of the hydraulic drop of the pumps:

(10)

there is n-quantity of the pumps, A (x) and B (x)-taking into consideration the effect of the hydrodynamic active admixture the empirical coefficient:

The necessary volume of the admixture may be determined on the basis of the balance of the hydraulic drop and pipeline:

(11)

there is Dh_x –suction head, that shall satisfy the condition:

(12)

there is p_k(x)-the pressure of the enriched steam of the solution, depending on the volume of the admixture, shall be determined on the formula:

(13)

there is r_н –the pressure of the saturated steams of the Newtonian components of the solution; r_к –the pressure of the saturated steams of the additives.

Equation of the hydraulic drop may be solved with use of the mathematical sets (MathCAD Maple, Mathematica) with use of the program means or graphical methods.

Conclusion

1. Formula for the determination of the objective concentration of the hydrodynamic active admixture on the basis of the balance of the hydraulic drop.

2. Equation of the balance of the hydraulic drop should be solved with use of the modern mathematical sets (MathCAD Maple, Mathematica), as well as graphical active methods.

References

1. Amirov F.A and others. Forecasting of the pump characteristics of the centrifugal pumping equipment under the operation of Newtonian solutions. Scientific records ISU # 1, Baku, 1999

2. Belousov Y.P. Antiturbulent additive for the hydrocarbon liquid. Novosibirsk, Nauka, 1986, page 145

3. Amirov F.A and others. Toms effect on vane pumps. AGNA, Baku, 2003, page 75

4. Amirov F.A, Agammadova S.A Toms effect ion Hydraulic systems, tenth Baku International Congress, Baku, 2009.

ОПРЕДЕЛЕНИЕ КОНЦЕНТРАЦИИ ГИДРОДИНАМИЧЕСКИ-

АКТИВНОЙ ДОБАВКИ ПРИ СОВМЕСТНОЙ РАБОТЕ

НАСОСА И ТРУБОПРОВОДА

Ф.А.Амиров, С.А.Агаммедова

Азербайджанская Государственная Нефтяная Академия

ВЫВОДЫ

1. На основании баланса напоров насоса и трубопровода получена формула для определения объемной концентрации гидродинамически-активной добавки.

2. Уравнение баланса напоров можно решить с использовании современных математических пакетов (MathCAD Maple, Mathematic), а также графоаналитическим методом.

Авторы:

1. Фикрет Алибаба оглы Амиров, (кандидат технических наук)

2. Севда Алипаша кызы Агаммедова. (доктор философии по технике)

Название статьи:

«Определение концентрации гидродинамически-активной добавки при совместной работе насоса и трубопровода»

Адрес:

г. Баку, AZ 1010, Проспект Азадлыг 20

Азербайджанская Государственная Нефтяная Академия (кафедра № 43)