УДК  519(0.75)

 

ВЕРОЯТНОСТЬ ПОПАДАНИЯ СЛУЧАЙНОЙ ТОЧКИ В ПОЛУПЛОСКОСТЬ ИЛИ ПРЯМОУГОЛЬНИК

 

Дюзбенбетов Б.Д., к.ф-м.н., доцент кафедры математики КазГосЖенПУ

Мелдебекова Г.К., бакалавр математики

 

     Методы теории вероятностей широко применяются в различных отраслях естествознания и техники: в теории надежности, в теории массового обслуживания, в теоретической физике, геодезии, астрономии, теории стрельбы, теории ошибок наблюдений, теории автоматического управления, общей теории связи и во многих других теоретических и прикладных науках. Теория вероятностей служит также для обоснования математической и прикладной статистики, которая в свою очередь используется при планировании и организации производства, при анализе технологических процессов, предупредительном и приемочном контроле качества продукции и для многих других целей.

      В последние годы методы теории вероятностей все шире и шире проникают в различные области науки и  техники, способствуя их прогрессу.

      Кроме одномерных случайных величин изучают величины, возможные значения которых определяются двумя, тремя,…,  числами. Такие величины называются соответственно двумерными, трехмерными,…, -мерными.

     Будем обозначать через  двумерную случайную величину. Каждую из величин  и   называют составляющей (компонентой); обе величины  и  , рассматриваемые одновременно, образуют систему двух случайных величин. Аналогично, - мерную величину можно рассматривать как систему случайных величин. Например, трехмерная величина  определяет систему трех случайных величин ,  и .

      Двумерную случайную величину   геометрически можно истолковать либо как случайную точку  на плоскости (т.е. как точку со случайными координатами), либо как случайный вектор . Трехмерную  случайную величину геометрически можно истолковать как точку  в трехмерном пространстве или как вектор .

     Целесообразно различать дискретные (составляющие этих величин дискретные) и непрерывные  (составляющие этих величин непрерывны) многомерные случайные величины.

      Законом распределения  дискретной двумерной случайной величины называют перечень возможных значений этой величины, т.е. пар чисел  и их  вероятностей  . Обычно закон распределения задают в виде таблицы с двойным входом (табл.1).

 

Таблица 1

 

			…		…
			…		…
…	…	…	…	…	…	…
			…		…
…	…	…	…	…	…	…
			…		…

 

     Первая строка таблицы содержит все возможные значения составляющей  , а первый столбец – все возможные значения составляющей . В клетке, стоящей на пересечений «столбца » и «строки », указана вероятность  того, что двумерная случайная величина примет значение  .

     Так как события  образуют полную группу, то сумма вероятностей, помещенных во всех клетках таблицы равна единице.

     Зная закон распределения двумерной дискретной случайной величины, можно найти законы распределения каждой из составляющих. Действительно, например, события , ,…,  несовместны, поэтому вероятность   того, что  примет значение  такова:

     Таким образом, вероятность того, что   примет значение  , равна сумме вероятностей  «столбца ». В общем случае, для того,  чтобы найти вероятность , надо просуммировать вероятности столбца . Аналогично сложив вероятности «строки », получим вероятность .

      Рассмотрим двумерную случайную величину  (безразлично, дискретную или непрерывную). Пусть , - пара действительных чисел. Вероятность события, состоящего в том, что  примет значение, меньшее , и при этом  примет значение, меньшее , обозначим через . Если  и  будут изменяться, то, вообще говоря, будет изменяться  и  , т.е.  есть функция от   и .

      Функцией распределения двумерной случайной величины   называют функцию , определяющую для каждой пары чисел  ,  вероятность того, что   примет значение, меньшее , и при этом  примет значение, меньшее :

      Геометрически это равенство можно истолковать так:  есть вероятность того, что случайная точка  попадает в бесконечный квадрат с вершиной , расположенный левее и ниже этой вершины (рисунок 1).

 

 

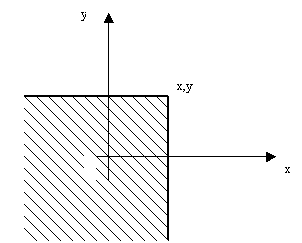
Рисунок 1

 

     Свойство 1. Значения функции распределения удовлетворяют двойному неравенству

.

      Свойство 2.  есть неубывающая функция по каждому аргументу, т.е.

                                   , если

                                   , если

     Свойство 3. Имеют место предельные соотношения:

1) ,         2) ,

                                3) ,       4) .

    Свойство 4. а) При  функция распределения системы становится функцией распределения составляющей  :

     б) При  функция распределения системы становится функцией распределения составляющей  :

.

      Используя функцию распределения системы случайных величин  и  , легко найти вероятность того, что в результате испытания случайная точка попадает в полуполосу  и (рисунок 2а) или в полуполосу  и  (рисунок 2б).

 

 

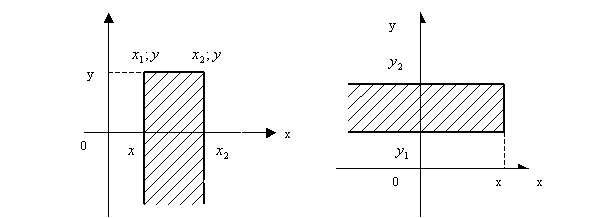
                                а)                                                       б)

 

Рисунок 2

 

     Вычитая из вероятности попадания случайной точки в квадрант с вершиной  вероятность попадания точки в квадрант с вершиной  (рисунок 2а), получим

     Аналогично имеем

.

     Таким образом, вероятность попадания случайной точки в полуполосу равна приращению функции распределения по одному из аргументов.

     Рассмотрим прямоугольник  со сторонами параллельными осям (рисунок 3). Пусть уравнения сторон таковы:

.

     Найдем вероятность попадания случайной точки  в этот прямоугольник.

     Искомую вероятность можно найти, например, так: из вероятности попадания случайной точки в полуполосу  с вертикальной штриховкой (эта вероятность равна ) вычесть  вероятность попадания точки в полуполосу  с горизонтальной штриховкой (эта вероятность равна ):

 

                                     (*)

 

 

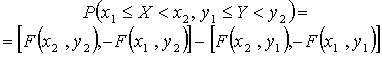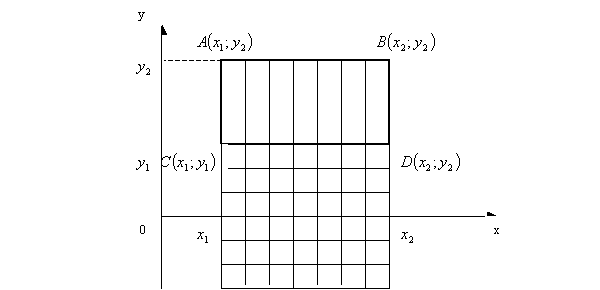
Рисунок 3

 

Литература

 

1.       В.Е. Гмурман Теория вероятностей и математическая статистика. М., 1972.

2.       Н. Арлей, К.Р.Бух.  Введение в теорию вероятностей и математическую статистику. ИЛ, 1961

3.       Вентцель Е.С. Теория вероятностей, изд.3, «Наука», 1964

4.       Л.З.Румшиский. Элементы теории вероятностей. изд.2, «наука», 1963