Лисенко В.В.
Запорізькій національний університет, Україна
Застосування методу Ліндштедта-Пуанкаре
при дослідженні вимушених нелінійних коливань
механічних систем з демпфіруванням
В роботі розглядається застосування методу Ліндштедта-Пуанкаре [1] при наближеному аналітичному розв’язанні задач Коші, які описуються нелінійними диференціальними рівняннями другого порядку у вигляді (1). До розв’язання нелінійних рівнянь зводиться, наприклад, процес розв’язання задачі о коливаннях прямокутної пластини методом Бубнова-Гальоркіна [2]. Методика розглядається як доповнення до гібридного підходу [3-5] до асимптотичного розв’язання рівнянь з параметрами.
Розглянемо вимушені нелінійні коливання механічної системи з однією ступеню вільності, яка описується нелінійним неоднорідним диференційним рівнянням другого порядку вигляду [6, 7]
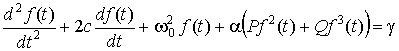 . (1)
. (1)
де ![]() – шукана функція, яка
характеризує відхилення системи від початку координат;
– шукана функція, яка
характеризує відхилення системи від початку координат; ![]() – зовнішня сила;
– зовнішня сила; ![]() – "малий"
параметр; c – коефіцієнт
демпфірування.
– "малий"
параметр; c – коефіцієнт
демпфірування.
Шукана функція f на початку цього
відрізка задовольняє деяким початковим умовам. Будемо розглядати тільки
такі задачі Коші, для яких розв’язок існує, і він єдиний.
Розглянемо, спочатку, випадок без демпфірування,
тобто ![]() . В основі методу Ліндштедта-Пуанкаре лежить ідея, почерпнута
з наступного спостереження: нелінійність змінює частоту коливань системи від
значення
. В основі методу Ліндштедта-Пуанкаре лежить ідея, почерпнута
з наступного спостереження: нелінійність змінює частоту коливань системи від
значення ![]() , що відповідає лінійній системі, до
, що відповідає лінійній системі, до ![]() , що відповідає нелінійній системі . Щоб урахувати цю зміну
частоти, Ліндштедт ввів нову змінну у вигляді [1]:
, що відповідає нелінійній системі . Щоб урахувати цю зміну
частоти, Ліндштедт ввів нову змінну у вигляді [1]:
![]() , (2)
, (2)
та розклав w та f по степеням параметру α:
![]() , (3)
, (3)
![]() , (4)
, (4)
де ![]() – частота коливань
лінійної системи без урахування демпфірування.
– частота коливань
лінійної системи без урахування демпфірування.
Підставляючи розклади (3), (4) в рівняння (1),
та прирівнюючи коефіцієнти при однакових степенях α, одержимо систему
рівнянь для визначення невідомих функцій ![]() , при чому
, при чому
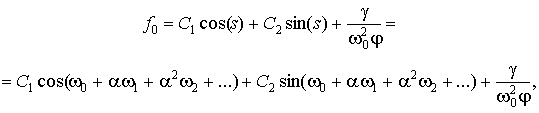 (5)
(5)
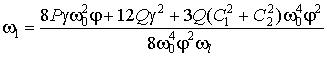 , (6)
, (6)
де ![]() ,
, ![]() – дійсні постійні
інтегрування.
– дійсні постійні
інтегрування. ![]() та
та ![]() визначаються з умов
відсутності секулярних членів у розв’язку f.
визначаються з умов
відсутності секулярних членів у розв’язку f.
Тепер розглянемо вимушені нелінійні коливання
механічної системи з демпфіруванням, тобто ![]() . При наявності демпфірування цю методику також можна
застосувати, та розклавши w по степеням
параметру α наступним чином:
. При наявності демпфірування цю методику також можна
застосувати, та розклавши w по степеням
параметру α наступним чином:
![]() , (7)
, (7)
де ![]() – частота коливань
лінійної системи з урахуванням демпфірування:
– частота коливань
лінійної системи з урахуванням демпфірування:
![]() . (8)
. (8)
Загальний розв’язок ![]() буде
буде
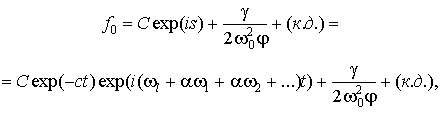 (9)
(9)
або в тригонометричному вигляді
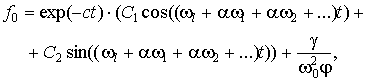 (10)
(10)
де (к.д.) – комплексно спряжений доданок, C – комплексна постійна інтегрування, ![]() ,
, ![]() – дійсні постійні
інтегрування, при чому
– дійсні постійні
інтегрування, при чому
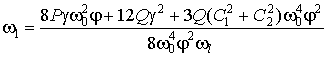 , (11)
, (11)
![]() ,
, ![]() . (12)
. (12)
Результати одержані у випадку коли всі
коефіцієнти вихідного рівняння ти зовнішня сила є постійні. Але отримані
формули можна використовувати і у випадку, коли коефіцієнти вихідного рівняння
та зовнішня сила є функціями часу. Напевно це має сенс, коли ці функції є
повільно змінними (повільно по відношенню до природної одиниці часу - періоду
власних коливань), тобто при ![]() , де
, де ![]() - малий параметр.
Нелінійні задачі динаміки, розв’язані авторами із застосуванням запропонованої
методики, підтверджують правильність цього припущення.
- малий параметр.
Нелінійні задачі динаміки, розв’язані авторами із застосуванням запропонованої
методики, підтверджують правильність цього припущення.
Література
1. Найфе А.Х. Методы возмущений / А.Х. Найфе; пер. с англ. – М. : Мир, 1976. –
456 с.
2. Вольмир А.С. Нелинейная динамика пластинок и оболочек / А.С. Вольмир. – М. : Наука, 1972. – 432 с.
3. Noor A.K.
Reduced basis technique for nonlinear analysis of structures / Noor A.K.,
Peters J.M. // Proc. of the AIAA-ASME-ASCE-AHS 20th Structures,
Structural Dynamics and Materials conference, St. Louis, USA, 1979. – P. 116 –
126.
4. Gristchak
V.Z. A hybrid WKB-Galerkin method and its application / Gristchak V.Z., Dmitrijeva Ye.M. //
Technishe Mechanik. – 1995. – №3. – Р. 281-294.
5. Geer J.F. A hybrid peturbation-Galerkin technique for differential equations containing a parameter / Geer J.F., Andersen C.M. // Applied Mechanics Reviews. – 1989. – №42(11). – P. S69-S77.
6. Gristchak
V.Z. WKB-Galerkin method with application to the correlation analysis of
stochastic behaviour of non-linear systems with time-depended parameters / Gristchak V.Z., Lysenko V.V. //
Computational Stochastic Mechanics, proceedings of the fourth international
conference on computational stochastic mechanics 9-12 june 2002, Corfu, Greece.
– Rotterdam: Millpress (Netherlands), 2003. – P. 243-248.
7. Gristchak
V.Z. Non-linear stochastic vibration
problems for the plates with time-dependent parameters / Gristchak V.Z., Lysenko V.V. / ICTAM-2004 : 21st
international congress of theoretical and applied mechanics, 15-21 august 2004, Warsaw, Poland. – Warsaw (Poland), 2004. – P.
367.