Шинкарик М.І.
Тернопільський національний
економічний університет
Обчислення невласних інтегралів за власними елементами
гібридного диференціального оператора Фур’є – Ейлера на полярній вісі ![]()
Побудуємо
обмежений на множині ![]() розв’язок сепаратної
системи модифікованих диференціальних рівнянь Фур’є та Ейлера
розв’язок сепаратної
системи модифікованих диференціальних рівнянь Фур’є та Ейлера
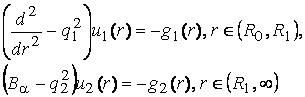 (1)
(1)
за умовами спряження
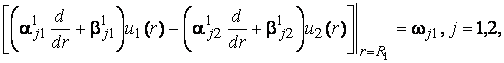 (2)
(2)
та крайовими умовами
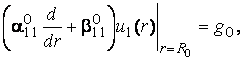
![]() (3)
(3)
У рівностях
(1) - (3) ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
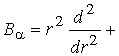
![]()
![]()
![]() - диференціальний оператор Ейлера [1].
- диференціальний оператор Ейлера [1].
Фундаментальну
систему розв’язків для диференціального рівняння Фур’є  утворюють функції
утворюють функції ![]() та
та ![]() [1]. Фундаментальну
систему розв’язків для диференціального рівняння Ейлера
[1]. Фундаментальну
систему розв’язків для диференціального рівняння Ейлера ![]() утворюють функції
утворюють функції ![]() та
та ![]() [1].
[1].
Наявність
фундаментальної системи розв’язків дозволяє будувати розв’язок крайової задачі (1)- (3) методом функцій Коші
[1,2]:
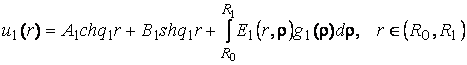 (4)
(4)
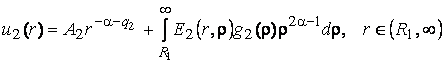 (5)
(5)
Тут ![]() - функції Коші [1,2]:
- функції Коші [1,2]:
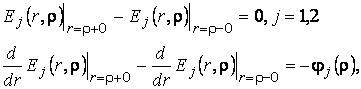 (6)
(6)
де ![]()
![]() .
.
Визначимо
функції:
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Безпосередньо
перевіряється, що функції Коші:
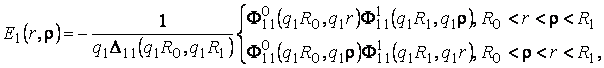 (7)
(7)
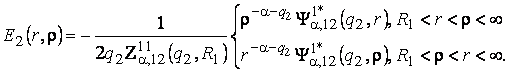 (8)
(8)
Умови спряження (2) та крайова
умова в точці ![]() для визначення
для визначення
величин ![]() та
та ![]() дають алгебраїчну
систему рівнянь:
дають алгебраїчну
систему рівнянь:
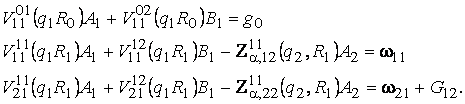 (9)
(9)
У системі (9)
бере участь функція
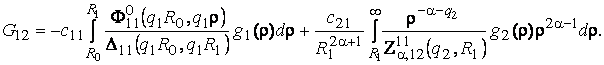
Припустимо,
що виконана умова однозначної розв’язності крайової задачі (1) – (3): визначник
алгебраїчної системи (9)
![]() (10)
(10)
Введемо до
розгляду головні розв’язки крайової задачі (1) – (3):
1) породжені
неоднорідністю системи (1)функції впливу
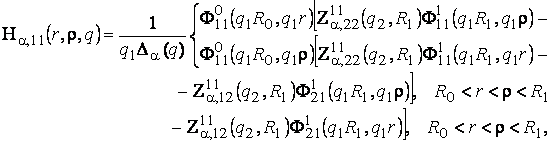
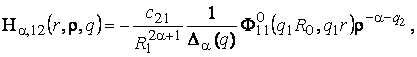
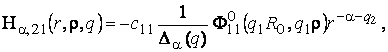 (11)
(11)
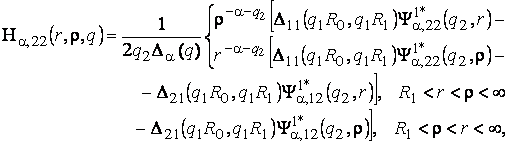
2) породжені
крайовою умовою в точці ![]() функції Гріна
функції Гріна
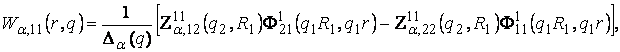
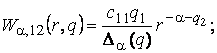 (12)
(12)
3) породжені
неоднорідністю умов спряження функції Гріна
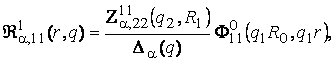
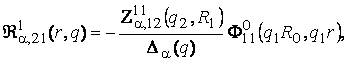 (13)
(13)
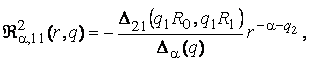
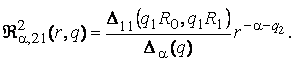
У результаті
однозначної розв’язності алгебраїчної системи (9), підстановки одержаних
значень ![]() ,
, ![]() та
та ![]() у рівності (4) маємо
єдиний розв’язок крайової задачі (1) - (3) :
у рівності (4) маємо
єдиний розв’язок крайової задачі (1) - (3) :
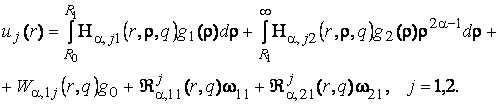 (14)
(14)
Побудуємо
розв’язок крайової задачі (1) - (3) методом гібридного інтегрального
перетворення типу Фур’є – Ейлера [3]:
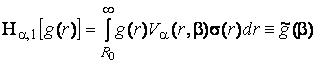 (15)
(15)
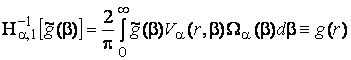 (16)
(16)
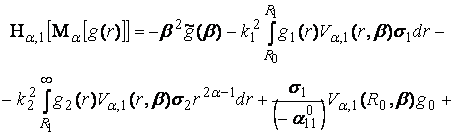
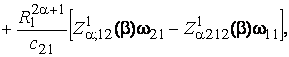 (17)
(17)
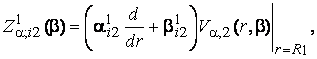
![]()
У рівностях
(15) – (17) беруть участь функції:
![]()
![]()
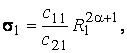
![]()
![]()
![]()
![]()
![]()
![]()
Інші величини
та функції загальноприйняті [4].
Єдиний
розв’язок крайової задачі (1) - (3),
побудований за відомою логічною схемою [4] методом інтегрального перетворення,
визначеного формулами (15) – (17), описують функції:
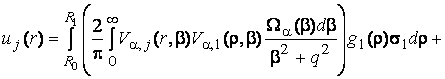
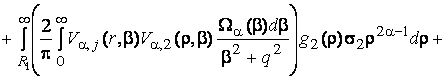 (18)
(18)
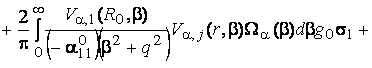
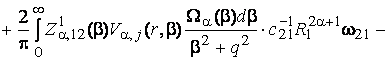
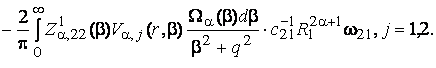
Порівнюючи
розв’язки (14) та (18) в силу єдності, маємо наступні формули обчислення
поліпараметричних невласних інтегралів за власними елементами гібридного
диференціального оператора:
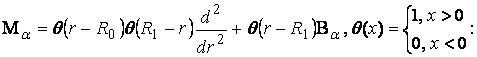
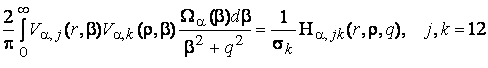 (19)
(19)
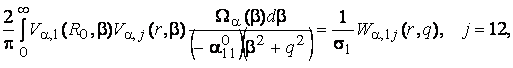 (20)
(20)
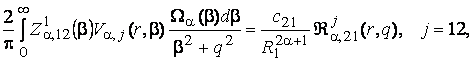 (21)
(21)
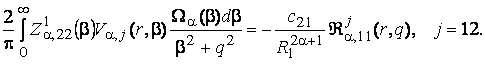 (22)
(22)
У рівностях
(18) – (22) ![]() якщо
якщо ![]() (
(![]()
![]() ), або
), або ![]() якщо
якщо ![]() (
(![]()
![]() ). Можна покласти
). Можна покласти ![]() (
(![]()
![]() ), звужуючи при цьому сім’ю невласних інтегралів.
), звужуючи при цьому сім’ю невласних інтегралів.
1.
Степанов В.В. Курс дифференциальных уравнений. – М.:
Физматгиз, 1959. – 468 с.
2.
Шилов Г.Е. Математический анализ. Второй специальный
курс. – М.: Наука, 1965. – 328 с.
3.
Ленюк М.П., Шинкарик М.І. Гібридні інтегральні
перетворення (Фур’є, Бесселя, Лежандра). Частина 1. – Тернопіль: Економічна
думка, 2004. – 368 с.
4.
Ленюк М.П. Обчислення невласних інтегралів методом
гібридних інтегральних перетворень (Фур’є, Бесселя, Лежандра). Том V. – Чернівці: Прут, 2005. – 368 с.