Искакова А. К.

Республика Казахстан, г. Алматы, Казахский государственный женский педагогический институт

Об одной многоточечной задаче

В статье рассматриваются задачи, содержащие в краевых условиях производные первого порядка, то есть порядок производной в краевых условиях равен порядку уравнения. Изучается общий случай корректности многоточечных краевых задач для системы дифференциальных уравнений. Известно, что многие краевые задачи для обыкновенных дифференциальных уравнений (систем уравнений) можно записать в виде краевой задачи для систем дифференциальных уравнений первого порядка. При изучении многоточечных краевых задач интересна лемма.

Лемма 1. Пусть F- линейный, непрерывный оператор из С[0,1]_n в C¹[0,1]_n, тогда задача

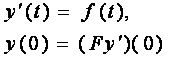(1)

корректна.

Нас интересуют многоточечные задачи. Возьмем точки , лежащие на [0,1]. Пусть – постоянные матрицы размерности , – переменные матрицы порядка , элементы которых лежат в С¹[0,1] - пространстве непрерывно дифференцируемых функций. Определим оператор F, действующий на f(t)C[0,1]_n по формуле

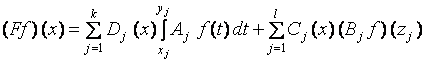(2)

Этот оператор действует из С[0,1]_n в С¹[0,1]_n при определении интеграла от х_j до y_j, если , как обычно принимаем

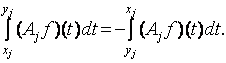
В следующих леммах выяснен произвол при составлении корректных многоточечных краевых задач.

Лемма 2. Пусть - произвольные точки отрезка [0,1], a - произвольные матрицы порядка , тогда задача

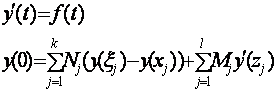(3)

в пространстве С[0,1]_n–корректна, mо eсть для любой функции fC[0,1]_n имеет единственное решение у(t) C¹[0,1]_n.

Следствие 1. Пусть F–оператор, определенный равенством (2), тогда задача (3) корректна.

Лемма 3. Пусть -произвольная матрица, -точки на [0,1], тогда задача

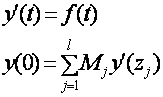, (4)

корректна.

Задача (3), как и задача (4), в краевых условиях содержит производные первого порядка, то есть порядок производной равен порядку уравнения. Это существенно отличает ее от традиционных задач, в которых в краевые условия входят производные более низкого порядка, чем порядок самого уравнения. Используя лемму 3, находим обобщение теоремы 1 на векторный случай.

Теорема 1. Пусть , - некоторые точки отрезка [0,1], a A₁, A₂, …, A_k; B₁, B₂, …, B матрицы порядка . Задача

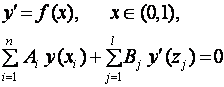
корректна, тогда и только тогда, когда , где .

Теорема 2. Существует число , такое, что если

то задача

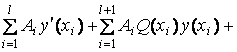
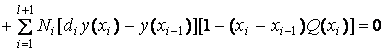
корректна при любом выборе матриц {A_i, N_i} и чисел {d_i}.

Приведем примеры корректных задач к теореме 1. Рассмотрим уравнение

(5)

Обозначим тогда уравнение (6) запишется в виде

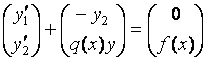
или

(6)

где Q(x) есть матрица:

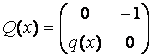
Утверждение. Многоточечная задача

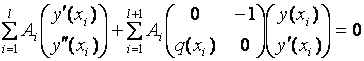
однозначно разрешима в пространстве дважды непрерывно дифференцируемых функций.

Здесь - произвольные матрицы второго порядка. Отметим, что при из теоремы 2 вытекает

Следствие 2. Существует малое число такое, что, если

то задача

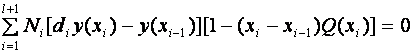
корректна при произвольных матрицах

ЛИТЕРАТУРА

1. Отелбаев М.О., Кокебаев Б., Шыныбеков А. К теории сужения и расширения операторов. Часть 2. Изв.АН КазССР, серия физико-математическая, 1982, 5, с.24-26.