Ленюк М.П.

Чернівецький національний університет імені Юрія Федьковича

Підсумовування функціональних рядів за власними елементами гібридного диференціального оператора (Конторовича-Лєбєдєва)-Ейлера на сегменті [R₀, R₂]

Побудуємо обмежений на множині I₁ = {r: r Î (0, R₁) (R₁, R₂), R₀ > 0, R₂ < ¥} розв’язок сепаратної системи диференціальних рівнянь Бесселя з виродженням при старшій похідній та Ейлера

, r Î (R₀, R₁),

, r Î (R₁, R₂) (1)

за крайовими умовами

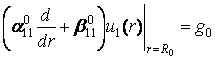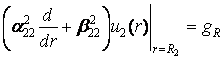, (2)

та умовами спряження

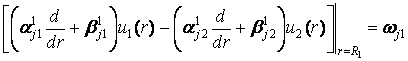, j = 1, 2. (3)

Умови на коефіцієнти загальноприйняті [1].

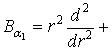
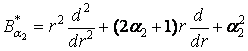Тут – диференціальний оператор Бесселя [1], а – диференціальний оператор Ейлера [2]; 2a_m + 1 > 0, l Î (0, ¥), m = 1, 2.

Фундаментальну систему розв’язків для рівняння Бесселя ()v = 0 утворюють модифіковані функції Бесселя v₁ = (lr) та v₂ = (lr) [1]; фундаментальну систему розв’язків для рівняння Ейлера утворюють функції v₁ = та v₂ = [2].

Наявність фундаментальної системи розв’язків дає можливість побудувати єдиний розв’язок крайової задачі (1) – (2) методом функцій Коші [2, 3]:

,

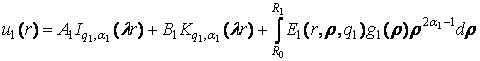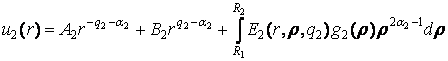. (4)

У рівностях (4) беруть участь функції Коші [2, 3]:

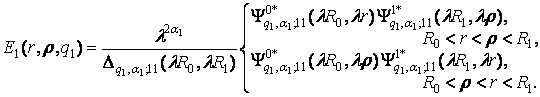(5)

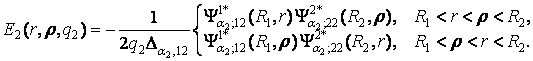(6)

У рівностях (5), (6) прийняті позначення:

, j = 1, 2;

, j = 1, 2.

Всі інші функції загальноприйняті [5].

Умови (2) та (3) для визначення величин A_j та B_j (j = 1, 2) дають неоднорідну алгебраїчну систему з чотирьох рівнянь:

,

– =

= w₁₁d_j1 + (w₂₁ + G₁₂)d_j2, j = 1, 2, (7)

,

Тут d_jk – символ Кронекера, а функція

G₁₂ = +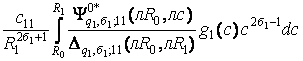

+ .

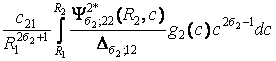Припустимо, що виконана умова однозначної розв’язності крайової задачі (1) – (3): для будь-якого ненульового вектора = {q₁; q₂} визначник алгебраїчної системи (7) повинен бути відмінним від нуля [4], тобто

D_(a)(q) º ¹ 0, q = (q₁, q₂), (a) = (a₁, a₂), (8)

Визначимо головні розв’язки крайової задачі (1) – (3):

1) породжені крайовою умовою в точці r = R₀ функції Гріна

,

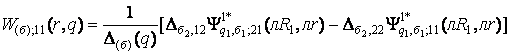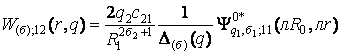; (9)

2) породжені крайовою умовою в точці r = R₂ функції Гріна

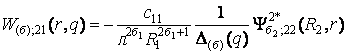, (10)

;

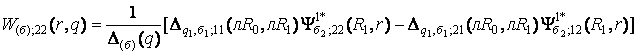3) породжені неоднорідністю умов спряження функції Гріна

, ,

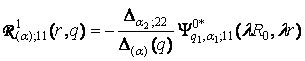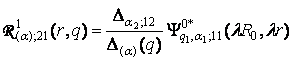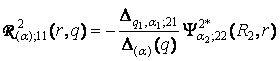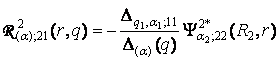; (11)

4) породжені неоднорідністю системи (1) функції впливу

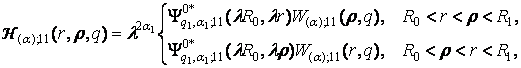
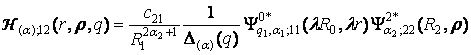
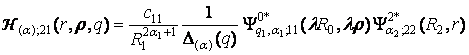, (12)

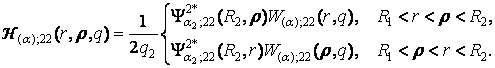
У результаті однозначної розв’язності алгебраїчної системи (7) та підстановки одержаних значень A_j, B_j у формули (4) маємо єдиний розв’язок крайової задачі (1) – (3):

u_j(r) = W_{(a), j1}(r, q)g₀ + W_{(a), j2}(r, q)g₀ + + +

+ +

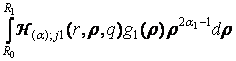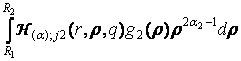+ , j = 1, 2. (13)

Побудуємо тепер розв’язок крайової задачі (1) – (3) методом інтегрального перетворення, породженого на множині I₁ гібридним диференціальним оператором (ГДО)

, (14)

де q(x) – одинична функція Гевісайда [3].

Власні елементи ГДО M_(a) знайдемо як розв’язок відповідної спектральної задачі Штурма-Ліувілля: побудувати на множині I₁ ненульовий розв’язок сепаратної системи звичайних диференціальних рівнянь

()V_{(a); 1}(r, b) = 0, r Î (R₀, R₁),

()V_{(a); 2}(r, b) = 0, r Î (R₁, R₂) (15)

за однорідними крайовими умовами

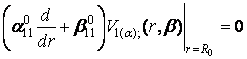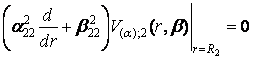, (16)

та однорідними умовами спряження

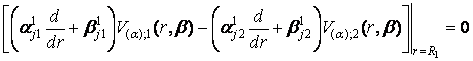, j = 1, 2. (17)

Тут b_j(b) = (b ² + )^1/2, ³ 0, j =1, 2.

Фундаментальну систему розв’язків для диференціального рівняння Бесселя ()v = 0 утворюють функції v₁(r) = (lr, b₁) та v₂(r) = (lr, b₁) [1]; фундаментальну систему розв’язків для диференціального рівняння Ейлера ()v = 0 утворюють функції v₁ = та v₂ = [2].

Якщо покласти

V_{(a); 1}(r, b) = A₁(lr, b₁) + B₁(lr, b₁),

V_{(a); 2}(r, b) = A₂cos(b₂ ln r) + B₂sin(b₂ ln r), (18)

то крайові умови (16) й умови спряження (17) для визначення величин A_j, B_j (j = 1, 2) дають однорідну алгебраїчну систему із чотирьох рівнянь:

,

– ,

, j = 1, 2. (19)

Алгебраїчна система (19) має ненульовий розв’язок тоді й тільки тоді, коли її визначник рівний нулю [4]:

= 0. (20)

Тут прийняті позначення:

, j = 1, 2;

, j = 1, 2.

Оскільки ГДО M_(a) самоспряжений і не має на I₁ особливих точок, то корені b_n трансцендентного рівняння (20) утворюють дискретний спектр [5].

У результаті розв’язання алгебраїчної системи (19) при b = b_n (b_j(b_n) º b_jn) стандартним способом [4] й підстановки одержаних значень A_j та B_j у формули (18) маємо компоненти V_{(a); j}(r, b_n) спектральної вектор-функції:

V_{(a); 1}(r, b_n) = ,

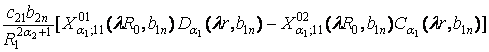V_{(a); 2}(r, b_n) = cos(b_2n lnr) –

– sin(b_2n lnr).

Наявність вагової функції

s(r) = q(r – R₀)q(R₁ – r)s ₁ + q(r – R₁)q(R₂ – r)s ₂,

де s₁ = , s₂ = 1, та спектральної вектор-функції V_(a)(r, b_т) = q(r – R₀)q(R₁ – r)V_{(a); 1}(r, b_n) + q(r – R₁) q(R₂ – r)s V_{(a); 2}(r, b_n) з квадратом норми

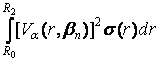= º +

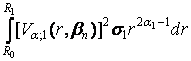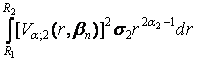+ (22)

дозволяє визначити пряме H_(a) та обернене скічненне гібридне інтегральне перетворення типу (Конторовича-Лєбєдєва)-Ейлера [5]:

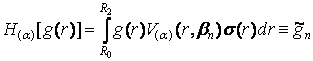, (23)

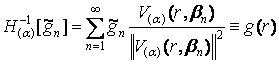, (24)

Побудований методом запровадженого формулами (23), (24) інтегрального перетворення єдиний розв’язок крайової задачі (1) – (3) має структуру [5]:

+

+ +

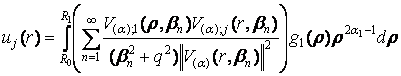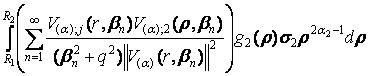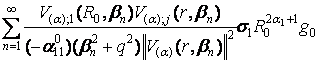+ + (25)

+ +

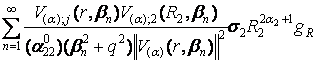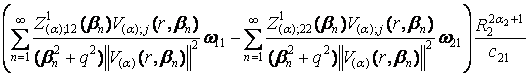+ , j = 1, 2.

Порівнюючи розв’язки (13) та (25) в силу єдиності, одержуємо наступні формули підсумовування поліпараметричних функціональних рядів:

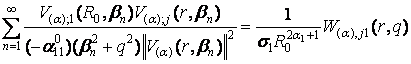; j = 1, 2, (26)

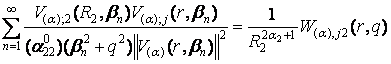; j = 1, 2, (27)

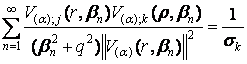
, j, k = 1, 2, (28)

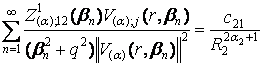
, j = 1, 2, (29)

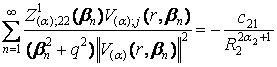
, j = 1, 2, (30)

q = {; }, , 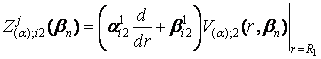i = 1, 2.

Підсумком викладеного вище є твердження.

Теорема. Якщо вектор-функція f(r) = {} неперервна на множин I₁, а функції g_j(r) задовольняють крайові умови (2) та умови спряження й виконується умова (8) однозначної розв’язності крайової задачі (1) – (3), то мають місце формули (26) – (30) підсумовування полі параметричних функціональних рядів за власними елементами ГДО .

1. Ленюк М.П., Міхалевська Г.І. Інтегральні перетворення типу Конторовича-Лєбєдєва – Чернівці: Прут, 2002. – 280 с.

2. Степанов В.В. Курс дифференциальных уравнений. – М.: Физматгиз, 1959. – 468 с.

3. Шилов Г.Е. Математический анализ. Второй специальный курс. – М.: Наука, 1965. – 328 с.

4. Курош А.Г. Курс высшей алгебры. – М.: Физматгиз, 1963. – 431 с.

5. Комаров Г.М., Ленюк М.П., Мороз В.В. Скінченні гібридні інтегральні перетворення, породжені диференціальними рівняннями другого порядку. – Чернівці: Прут, 2001. – 228 с.