Физика /1. Теоретическая физика

К.ф.-м.н., доцент Сидоренков В.В.

МГТУ им. Н.Э. Баумана, Россия

Структура электродинамических полей

и анализ их распространения в виде плоских волн

В настоящее время установлено [1, 2], что в отношении полноты охвата явлений электромагнетизма система уравнений электродинамики Максвелла электромагнитного (ЭМ) поля с компонентами электрической и магнитной напряженности:

(a) , (b) , (1)

(c) , (d) ,

не является единственной, и существуют другие системы полевых уравнений, концептуально необходимые для адекватного реальности анализа электродинамических процессов в материальных средах. Уравнения в этих системах рассматривают такие области пространства, где присутствуют либо только поле ЭМ векторного потенциала с электрической и магнитной компонентами:

(a) 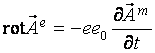, (b) , (2)

(c) , (d) ;

либо электрическое поле с компонентами и :

(a) , (b) , (3) (c) , (d) ;

либо, наконец, магнитное поле с компонентами и :

(a) , (b) , (4)

(c) , (d) .

Здесь - постоянная времени релаксации электрического заряда в среде за счет ее электропроводности.

Системы указанных уравнений и непосредственно следующие из них соотношения баланса:

для потока ЭМ энергии из уравнений (1)

, (5)

для потока момента ЭМ импульса из уравнений (2)

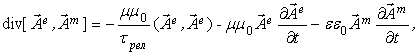(6)

для потока электрической энергии из уравнений (3)

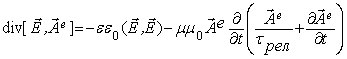(7)

и для потока магнитной энергии из уравнений (4)

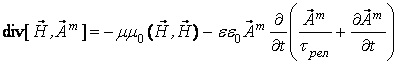(8)

однозначно доказывают, что, наряду с ЭМ полем с векторными компонентами и , существуют и другие поля: поле ЭМ векторного потенциала с компонентами и , электрическое поле с компонентами и , магнитное поле с и . Как видим, данный материал концептуально серьезно развивает основы теории электричества. В частности, в природе нет электрического, магнитного или другого электродинамического поля с одной компонентой. Структура электродинамического поля из двух векторных взаимно ортогональных компонент – это объективный способ его реального существования, принципиальная и единственная возможность распространения потока соответствующей физической величины посредством поперечных волн такого поля.

Поскольку структурная симметрия уравнений систем (1) и (2) математически тождественна, а волновые решения уравнений (1) известны [3], то далее анализ условий распространения, например, плоских электродинамических волн в однородных изотропных материальных средах проведем, прежде всего, для уравнений систем (3) и (4). Их необычные структуры между собой также тождественны, а волновые решения этих уравнений обсуждаются впервые.

Итак, рассмотрим волновой пакет плоской линейно поляризованной электрической волны с компонентами и для системы (3) либо магнитной волны с и для системы (4), которые представим комплексными спектральными интегралами. Тогда, например, для уравнений электрического поля:

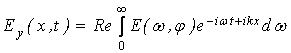и , где и - комплексные амплитуды.

Подставляя их в уравнения (3a) и (3c), приходим к соотношениям 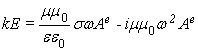и . Соответствующая подстановка интегралов и в уравнения (4а) и (4c) дает и . В итоге получаем общее для обеих систем выражение:

В конкретном случае среды идеального диэлектрика () из с учетом формулы следует обычное дисперсионное соотношение [3], описывающее однородные плоские волны электрического или магнитного полей. При этом связь комплексных амплитуд компонент указанных волновых полей имеет специфический вид:

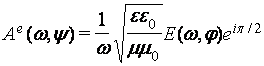и 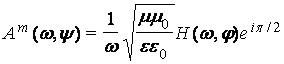, то есть

при распространении в диэлектрической среде компоненты поля сдвинуты между собой по фазе на π/2. Здесь специфика состоит в том, что в любой точке пространства характер поведения компонент поля такой волны аналогичен кинематическим параметрам движения (смещение и скорость) классической частицы в точке устойчивого равновесия поля потенциальных сил.

Для проводящей среды в асимптотике металлов () дисперсионное соотношение систем уравнений (3) и (4) имеет обычный в таком случае вид , где [3]. Тогда связи комплексных амплитуд решений систем (3) и (4) представятся в форме: 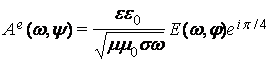и 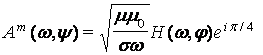, а волновые решения запишутся в виде экспоненциально затухающих в пространстве плоских волн со сдвигом фазы между компонентами поля на π/4.

Аналогичные рассуждения для рассматриваемого выше пакета плоской волны с компонентами и в системе (1) дают и , а для и в системе (2) имеем и 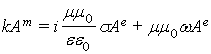. Таким образом, для этих двух систем электродинамических уравнений снова получаем выражение

В случае диэлектрической среды () дисперсионное соотношение для систем уравнений (1) и (2) есть при комплексных амплитудах: 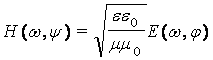и 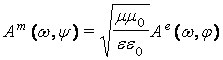, где сами решения описывают плоские однородные волны, компоненты поля которых синфазно распространяются в пространстве.

Для проводящей среды в асимптотике металлов () связь комплексных амплитуд для волновых решений систем (1) и (2) представятся выражениям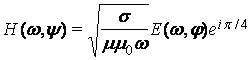и: и 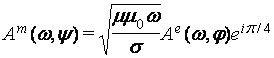, и решения запишутся как экспоненциально затухающие в пространстве плоские волны со сдвигом фазы между компонентами их полей на π/4. Следовательно, условия распространения в металлах волн всех четырех электродинамических полей подчиняется известному и теоретически хорошо изученному закону для плоских волн ЭМ поля в металлах [3].

Следует также отметить, что именно уравнения поля ЭМ векторного потенциала (2) описывают волны, переносящие в пространстве поток момента ЭМ импульса, которые еще со времен Пойнтинга безуспешно пытаются описать с помощью уравнений ЭМ поля (1) (см., например, результаты анализа в [4]). При этом волны ЭМ векторного потенциала не переносят энергии, поскольку в уравнениях (2) поля и отсутствуют. В этой связи укажем на пионерские работы [5], где обсуждаются неэнергетическое (информационное) взаимодействие поля векторного потенциала со средой при передаче таких волн и способ их детектирования посредством эффекта, аналогичного эффекту Ааронова-Бома.

Литература:

1. Сидоренков В.В. // Вестник МГТУ им. Н.Э. Баумана. Сер. Естественные науки. 2005. № 2. С. 35-46; 2006. № 1. С. 28-37.

2. Сидоренков В.В. // // Труды IV Всероссийской конференции «Необратимые процессы в природе и технике». М.: МГТУ, ФИАН, 2007. С. 173-180; // Материалы VII Международной конференции «Действие электромагнитных полей на пластичность и прочность материалов». Ч. 1. Воронеж: ВГТУ, 2007. С. 93-104; // Материалы IX Международной конференции «Физика в системе современного образования». Санкт-Петербург: РГПУ, 2007. Т. 1. Секция “Профессиональное физическое образование”. С. 127-129.

3. Матвеев А.Н. Электродинамика. М.: Высшая школа, 1980. 383 с.

4. Соколов И.В. // УФН. 1991. Т. 161. № 10. С. 175-190.

5. Чирков А.Г., Агеев А.Н. // ФТТ. 2002. Т. 44. Вып. 1. С. 3-5; 2007. Т. 49. Вып. 7. С. 1217-1221.