Економічні науки/8. Математичні методи в економіці

К.е.н. Снитюк О.І., к.е.н. Бережна Л.В.

Черкаський державний технологічний університет, Україна

Метод групового врахування аргументів як елемент технології прогнозування економічних процесів

Для України, яка перебуває на стадії трансформації економічної системи, проблеми прогнозування й аналізу економічних процесів є особливо актуальними. Необхідно звернути увагу на те, що в умовах наявності кризових явищ в економіці, домінування глобалізаційних процесів економічне прогнозування вимагає нових підходів.

Досліджуючи сучасні тенденції розвитку економічних процесів, можна виділити основні їх характеристики: складність, мінливість, невизначеність, нелінійність тощо. Ще один аспект, на який необхідно звернути увагу, – обмеження на отримання інформації на основі спостережень, тобто «мала» вибірка ретроспективних даних для побудови прогнозної моделі. Застосування в таких умовах класичних методів прогнозування обмежене. Зростає об’єктивна необхідність розробки і застосування сучасних моделей та методів прогнозування економічних процесів, які б в таких умовах суттєво покращували прогнозні оцінки, підвищували їх ефективність та достовірність.

Впродовж останніх десятиліть технології прогнозування інтенсивно розвиваються. Розроблено сотні різних методів та моделей, проте на практиці в економічному прогнозуванні застосовують всього 15-20 класичних моделей.

До найбільш поширених у практичній реалізації класичних моделей належать [1]: адаптивні моделі прогнозування, експертні моделі прогнозування, економетричне моделювання, зокрема, трендові моделі прогнозування (побудова моделей за допомогою оцінювання параметрів із застосуванням регресійного аналізу) тощо. Вказані методи належать до дедуктивних, методологiя яких полягає у переходi «вiд загального до конкретного», тобто вiд вивчення загальних закономірностей до побудови моделей конкретних процесів. При застосуванні цих методів значною проблемою є вибір структури моделі. Відповідальність за цей вибір лежить на конкретному аналітику.

Така проблема зникає при застосуванні індуктивного підходу до моделювання економічних процесів, який базується на принципі «вiд конкретного до загального», тобто вiд одержання емпiричних даних про поведiнку конкретних процесiв до побудови моделей iз застосуванням спеціальних програмних модулів, які максимально використовують інформацію вихідного вектора даних.

Сучасними моделями та методами прогнозування, які використовують індуктивний підхід і, на нашу думку, не достатньо оцінені та реалізовані в економічному прогнозуванні, є методи та моделі, в основі яких лежать інтелектуальні технології, зокрема, нейромережні методи, еволюційне моделювання та методи самоорганізації: метод групового врахування аргументів (МГВА) [2], генетичні алгоритми (ГА) [3], штучні нейронні мережі (НМ) [3].

Наведемо коротку характеристику методу групового врахування аргументів (МГВА) як одного з сучасних методів, який потребує більш інтенсивного практичного залучення в сферу економічного прогнозування.

Автором методу групового врахування аргументів є академік НАН України О. Г. Івахненко. МГВА є типовим методом індуктивного моделювання і одним з найбільш ефективних методів структурно-параметричної ідентифікації складних об'єктів, процесів і систем за даними спостережень в умовах неповноти інформації. Ефективність методу багато разів підтверджувалась розв'язанням конкретних задач з областей екології, економіки тощо. МГВА є методом пошуку закономірностей з автоматичним вибором структури і параметрів моделі на основі вибірки статистичних даних. Необхідно зауважити, що цей метод може бути застосований на «коротких» вибірках. В його основу покладено принципи зовнішнього доповнення, автоматичної генерації та послідовної селекції ускладнюваних структур моделей.

Нехай необхідно ідентифікувати залежність:

, де – вихідна результуюча характеристика; – вхідні фактори, Ідентифікація виконується за допомогою полінома Колмогорова-Габора

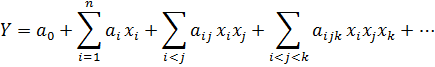
Відомо, що при збільшенні порядку полінома точність наближення ним спочатку зростає, а потім спадає. МГВА визначає оптимальну за складністю структуру моделі, адекватну вхідній вибірці даних. Для завершення селекції пошуку вказаної моделі та перевірки її на оптимальність в залежності від типу задачі використовують один із зовнішніх критеріїв: регулярності, незміщеності та балансу змінних. Теоретичні аспекти МГВА розглянуто в [2, 4].

Перешкодою до практичної реалізації МГВА економічними аналітиками є відсутність модулів програм МГВА у відомих пакетах програмного забезпечення, зокрема в EXCEL, SPSS, SAS, Statistica, Forecast Pro, Forecast Expert тощо.

Заслуговує на увагу інтерактивна програмна система АСТРІД,
яка призначена для побудови математичних моделей складних об’єктів і процесів за експериментальними даними в умовах невизначеності з метою виявлення закономірностей, ідентифікації, прогнозування, імітаційного моделювання, оптимізації та управління. Система є реалізацією ідей і алгоритмів методу групового врахування аргументів (МГВА) у вигляді діалогового пакету програм, доступного користувачам різного рівня підготовленості.

Таким чином, МГВА використовують для структурної, параметричної ідентифікації та прогнозування. Він базується на самоорганізації моделей і спрямований на визначення структури моделі оптимальної складності (на відміну від регресійних і трендових моделей, де структура моделі фіксована і визначається аналітиком). Підхід самоорганізації, реалізований в МГВА, базується на переборі моделей, які поступово ускладнюються, і виборі найкращого розв’язку згідно з мінімумом значення зовнішнього критерію. Комп’ютер (відповідне програмне забезпечення) знаходить оптимальну структуру моделі, при цьому мінімізується роль впливу аналітика на результати моделювання.

Оптимальним варіантом в економічному прогнозуванні є поєднання класичних та сучасних методів та моделей, серед яких вагоме місце займає МГВА.

Література

1. Бережна Л. В., Снитюк О. І. Економіко-математичні методи та моделі у фінансах. – К: Кондор, – 2009. – 301 с.

2. Ивахненко А. Г. Долгосрочное прогнозирование и управление сложными системами. – К.: Техніка, 1975. – 312 с.

3. Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности. /Вороновский Г.К., Махотило К.В., Петрашев С.Н., Сергеев С.Н. – Харьков: Основа, 1997. – 112 с.

4. Ивахненко А. Г., Степашко В. С. Помехоустойчивость моделирования. Киев: Наук. думка, 1985. - 216 с.