Cовременные информационные технологии/

Вычислительная техника и программирование

Камешова С.С., магистр естественных наук

Рауыл О., студент 1-го курса специальности «Информатика»

Костанайский государственный университет имени А. Байтурсынова, Костанай, Казахстан.

НЕЙРОННЫЕ СЕТИ КОХОНЕНА

Нейронные сети Кохонена - это класс нейронных сетей, основным элементом которых является слой Кохонена. Слой Кохонена состоит из адаптивных линейных сумматоров («линейных формальных нейронов»). Как правило, выходные сигналы слоя Кохонена обрабатываются по правилу «победитель забирает всё»: наибольший сигнал превращается в единичный, остальные обращаются в ноль.

Для наглядности все выкладки будут даваться для двумерных входных векторов. На рисунке 1 цветом изображен входной вектор. Каждый нейрон слоя Кохонена (как в принципе и любого другого слоя) просто суммирует вход, умножая его на свои веса. На самом деле веса слоя Кохонена есть не что иное как координаты вектора для данного нейрона. 

Таким образом, выход каждого нейрона Кохонена – это скалярное произведение двух векторов. Из геометрии мы знаем, что максимальное скалярное произведение будет в том случае, если угол между векторами будет стремиться к нулю (косинус угла будет стремиться к 1). Из этого следует, что максимальное значение будет иметь тот нейрон слоя Кохонена, который ближе всех к входному вектору.

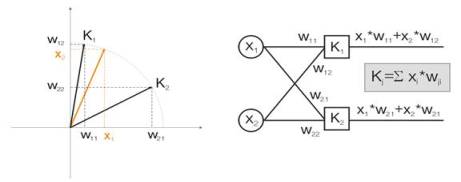
Рис.1 Победителем является тот нейрон, чей вектор наиболее близок ко входному сигналу. 

Как следует дальше из понятия, мы должны найти среди всех нейронов максимальное выходное значение, присвоить его выход единице, остальным нейронам присвоить ноль. Таким образом, слой Кохонена будет выдавать нам "ответ", в какой области пространства лежит входной вектор.

Целью обучения слоя является четкая пространственная классификация входных векторов. А это означает, что каждый нейрон должен отвечать за свой определенный участок, в котором он является победителем. Ошибка отклонения нейрона-победителя от входного вектора должна быть меньше, чем у остальных нейронов. Чтобы достичь этого, нейрон-победитель "поворачивается" в сторону входного вектора. 
На рисунке 2 показано разделение двух нейронов (черные векторы) для двух входных векторов (они обозначены цветом).

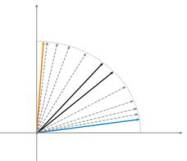
Рис.2. Каждый из нейронов приближается к своему ближайшему входному сигналу.

С каждой итерацией нейрон-победитель приближается к "своему" входному вектору. Его новые координаты определяются по формуле:

где A(t) - параметр скорости обучения, зависящий от времени t. Это невозрастающая функция, которая уменьшается с каждой итерацией от 1 до 0. Если начальное значение А=1, то корректировка веса происходит в один этап. Это возможно, когда для каждого входного вектора имеется один нейрон Кохонена (например, 10 входных векторов и 10 нейронов в слое Кохонена). 

Но на практике такого случая практически не встречается, так как обычно требуется большой объем входных данных разделить на группы схожих, тем самым уменьшив разнообразие входных данных. Поэтому значение А=1 нежелательно. Оптимальным на практике оказываются начальные значения менее 0.3. 

К тому же А обратно пропорционально числу входных векторов. То есть, желательно при большой выборке делать маленькие коррекции, чтоб нейрон-победитель не "летал" по всему пространству в своих корректировках. В качестве функционала А обычно выбирается любая монотонно убывающая функция. Например, гипербола или линейное убывание, или гауссовская функция.
На рисунке 3 показан шаг коррекции весов нейрона со скоростью А=0.5. Нейрон приблизился к входному вектору, ошибка уменьшилась.

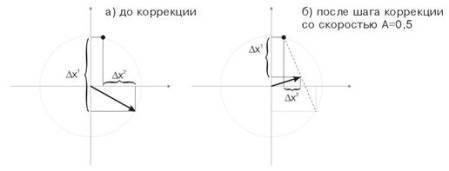
Рис.3. Коррекция весов нейрона под воздействием входного сигнала.

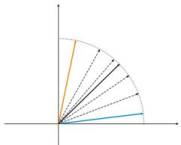
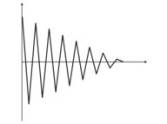
Рис.4. Колебания нейрона между двумя входными векторами.

На рисунке 4 (слева), имеется два входных вектора (обозначены цветом) и всего один нейрон Кохонена. В процессе коррекции нейрон будет качаться от одного входного вектора до другого (пунктирные линии). И по мере уменьшения значения А до 0 стабилизируется между ними. Изменения координат нейрона от времени можно охарактеризовать зигзагообразной линией (рисунок 4 справа).

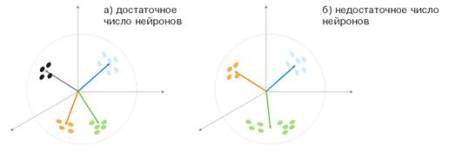
Рис. 5. Зависимость вида классификации от числа нейронов

Еще одна ситуация показана на рисунке 5. В первом случае четыре нейрона адекватно разделяют выборку на четыре области гиперсферы. Во втором случае недостаточное число нейронов приводит к увеличению ошибки и переклассификацию выборки. Таким образом, можно сделать вывод, что в слое Кохонена должно быть достаточное число свободных нейронов, которое зависит от объема классифицируемой выборки.

Литература

1. Бэстенс Д.-Э., Ван ден Берг В.-М., Вуд Д. Нейронные сети и финансовые рынки: принятие решений в торговых операциях. – М.: ТВП, 1997. – хх. – 236 с.
2. Вороновский Г.К. и др. Генетические алгоритмы, искусственные нейронные сети и проблемы виртуальной реальности. – Х.: Основа, 1997. – 112 с.
3. www.wikipedia.org