Кейбір күрделі тригонометриялық
теңсіздіктерді шешуі әдістері
Бұл
мақалада оқушыларға шығаруда қиындық
туғызатын кейбір тригонометриялық теңсіздіктіктерді
қарастыруды жөн көрдім.
1 мысал. ![]() теңсіздігін шешу керек.
теңсіздігін шешу керек.
Шешуі. Теңсіздіктің сол
жағын түрлендіре отырып, аламыз
![]()
![]() болсын. Онда
теңсіздігіміз келесі түрге келеді:
болсын. Онда
теңсіздігіміз келесі түрге келеді:
![]() , бұдан
, бұдан
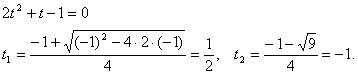
![]() болғандықтан,
болғандықтан, ![]()
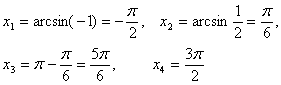
Жауабы: ![]()
![]()
2мысал. ![]() теңсіздігін шешу керек.
теңсіздігін шешу керек.
Шешуі. Теңсіздіктің сол
жағында
![]() алмастыра отырып, аламыз
алмастыра отырып, аламыз
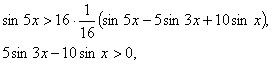
![]() формуласымен алмастырсақ,
формуласымен алмастырсақ,
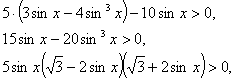
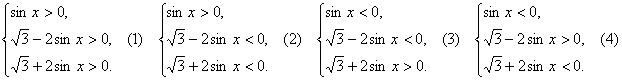 (1) теңсіздіктер жүйесін
қарастырайық.
(1) теңсіздіктер жүйесін
қарастырайық.
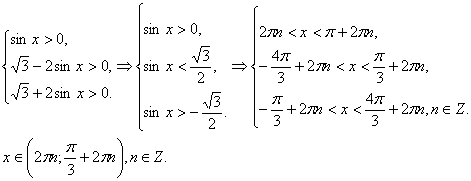
(2) теңсіздіктер жүйесін қарастыратын болсақ.
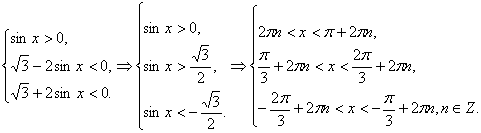
(2) теңсіздіктер жүйесін
қанағаттандыратын шешім жоқ.
(3) теңсіздіктер жүйесін
қарастырайық.
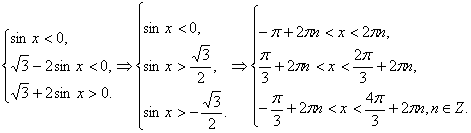
(3) теңсіздіктер жүйесін
қанағаттандыратын шешім жоқ.
(4) жүйені қарастыратын болсақ.
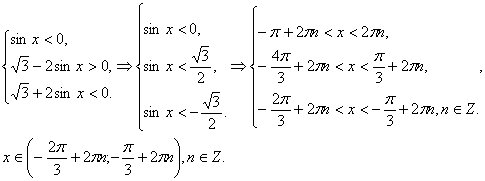
Жауабы: ![]() .
.
3 мысал. ![]() теңсіздігін шешу керек.
теңсіздігін шешу керек.
Шешуі. 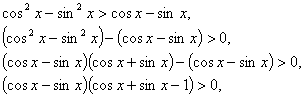
бұдан ![]() және
және ![]()
теңсіздіктер жүйесін аламыз.
Қосымша бұрыш енгізу арқылы
шығаратын болсақ, (1) теңсіздіктердің екі жағын
да ![]() бөлсек, аламыз
бөлсек, аламыз
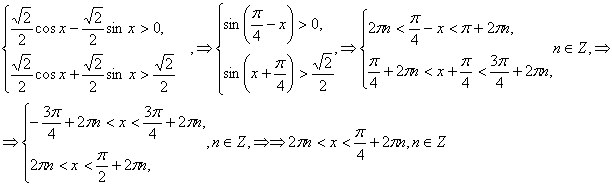 (2) жүйені қарастырайық,
мұнда да (1) жүйені шешкендегі әдісті қолданамыз, сонда
(2) жүйені қарастырайық,
мұнда да (1) жүйені шешкендегі әдісті қолданамыз, сонда
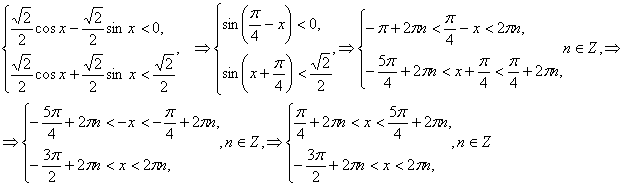 (2) қанағаттындыратын шешім жоқ.
(2) қанағаттындыратын шешім жоқ.
Жауабы: ![]()
![]()
4 мысал. ![]() теңсіздігін шешу керек.
теңсіздігін шешу керек.
Шешуі. ![]() формуласын қолдана
отырып, аламыз
формуласын қолдана
отырып, аламыз
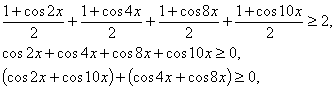
![]()
Косинустардың қосындысын түрлендіре
отырып, табамыз
![]() ,
,
жақша ішіндегі косинустардың қосындысын
түрлендірсек, теңсіздігіміз келесі түрге келеді, ![]() , бұдан
, бұдан
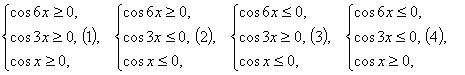
жүйелерін аламыз.
(1) жүйені қарастырайық.
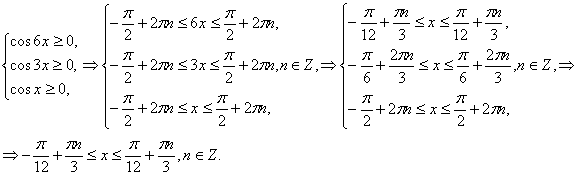
(2) жүйені қарастырайық.
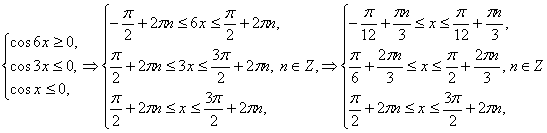
Соңғы жүйені
қанағаттандыратын шешім жоқ.
(3) жүйені қарастырайық.
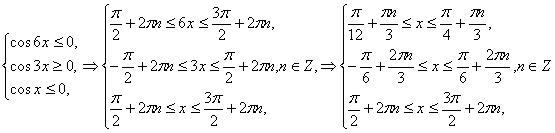
(3)жүйені қанағаттандыратын шешім
жоқ.
(4) жүйені қарастырайық.
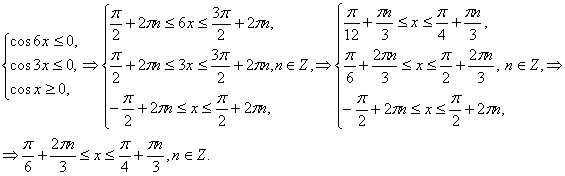
Жауабы: ![]() .
.
Әдебиеттер
тізімі:
1.
В.Г.Болтянский,
Ю.В.Сидоров, М.И.Шабунин Лекции и задачи по элементарной математике.М., 1972.
2.
С.Н.Новоселов.
Специальный курс тригонометрии. Высшая школа, 1959.
3.
П.Б.Талочкин.
Неравества и уравнения. Упрахнения и методические указания.М., Просвещение,
1970.