Физика, физика твердого тела

Влияние условия сохранения макросимметрии на температурную зависимость параметров решетки сегнетоэластической фазы при структурных фазовых переходах 4/mF2/m и

Д. ф.-м.н. Непочатенко В.А, ас. Непочатенко И.А.

Белоцерковский национальный аграрный университет, Украина

При полиморфных фазовых переходах с понижением симетрии в сегнето-эластиках и многоосных сегнетоелектриках образуется доменная структура с различными ориентационными состояниями (ОС) [1, 2]. В сегнетофазе существуют спонтанные повороты кристаллографических осей, обусловленные смещениями атомов и поворотами групп атомов (тетраэдров, октаэдров) при изменении температуры [3,4,5]. В результате этого образуются близкие ориентационные состояния (субориентационные), которые отличаются направлением спонтанного поворота [5-7]. Разные ОС можно совместить с помощью элементов симметрии парафази, которые утрачиваются, а субориентационные – не утрачиваются при структурном фазовом переходе [1, 2, 8]. Количество возможных ОС определяется симметрией парафазы [8].

Из модели доменной стенки [9,10] получено, что параметрам решетки сегнетофазы должны соответствовать определенные за величиной и знаком спонтанные повороты кристаллографических осей смежных доменов. Ориента-ционное согласование между различными ОС в полидоменном кристалле будет выполняться, когда спонтанные повороты, обусловленные структурой доменной стенки, будут равны спонтанным поворотам кристаллографических осей при любой температуре сегнетофазы [11]. То есть, в кристалле должны выполняться опреде-ленные соотношения между величинами параметров решетки, в противном случае полидоменный кристалл разрушится.

В связи с этим, представляет интерес исследовать, как влияет условие сохранения макросимметрии парафази в полидоменном кристалле [12] на температурную зависимость параметров решетки при фазовых переходах 4/mF2/m и на примере сегнетоэластиков BiVO₄ и

Монокристал BiVO₄ является сегнетоэластиком, в котором при температуре ~ наблюдается фазовый переход второго рода 4/mF2/m из високотемпера-турной параеластичної β-фази в моноклинную сегнетоеластическую α-фазу [13,14]. В параэластической фазе ориентация кристаллографической системы координат является стабильной (не зависит от температуры), поскольку нет спонтанных поворотов осей. В сегнетоеластичній фазе возможны четыре ОС, среди которых есть субориентационные [4,15]. Субориентационные состояния отличаются знаком спонтанного поворота вокруг оси симметрии 4-го порядка парафази. Величину спонтанного поворота можно определить из уравнений доменной стенки в двух системах координат (парафазы и сегнетофазы) [16, 17]:

(1)

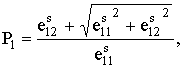
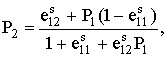
где компоненти тензора спонтан-ной деформации.

Тензоры теплового расширения, которые соответствуют двум субориента-ционным состояниям , в системе координат парафазы имеют вид:

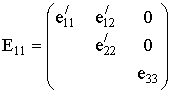
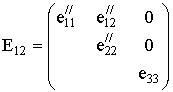(2)

где

Тензоры теплового расширения двух других ОС можно получить из (2), учитывая симметрию парафази (поворот на вокруг оси 4-го порядка парафази).

Из условия сохранения макросимметрии в полидоменном кристалле [12] для фазового перехода 4/mF2/m получаем усредненный тензор теплового расширения E_u для возможных четырех ОС:

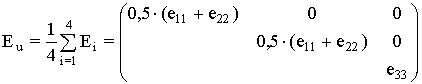. (3)

Тензор Е_u соответствует симметрии параеластичної фазы и совпадает с тензором secondary strains [18].

Из тензора E_u и (2) получаем кристаллографические параметры тетрагональ-ной решетки a_u и c_u усредненного полидоменного кристалла:

(4)

где а_m, b_m, с_m, γ– параметри моноклинной решетки, .

Согласно экспериментальной температурной зависимости кристаллографи-ческих параметров решетки BiVO₄ [19] и вычисленных значений а_u (рис.1, 2), можно сделать вывод, что в параэластической фазе тетрагональные параметры а_t и с_t имеют зависимость от температуры блискую к линейной, а в сегнетоэласти-ческой фазе моноклинные параметры а_m і b_m имеют нелинейную зависимость, а с_m і а_u – близкую к линейной зависимости.

Поскольку параметры а_m і имеют нелинейную зависимость, а их полусумма (4) является близкой к линейной, то их температурной зависимости соответствует алгебраическая сумма двух аналитических функцій:

(5)

где – соответствует температурной зависимости параметра а_u; характеризует нелинейный вклад при температурном изменении параметров решетки, обусловленный перераспределением деформаций между параметрами а_m и из-за смещения атомов и поворотов групп атомов при изменении спонтанной деформации. Согласно (3), (4), это явление не должно происходить в направлении оси с_m за счет других параметров, что согласуется с экспериментальными данными (рис. 2)

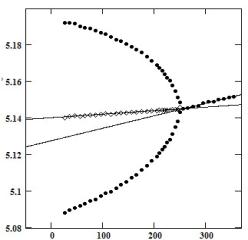
Рис.1. Температурная зависимость параметров решетки а_m(1), b_m(2), a_u(3) в сегнетоэластической фазе и а_t (4) в параэластической фазе BiVO₄.

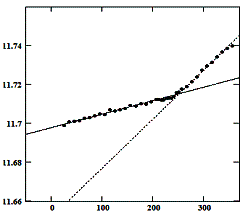
Рис.2. Температурная зависимость параметров решетки с_m(1) в сегнетоэластической фазе и с_t (2) в параэластической фазе BiVO₄.

Аналогичные исследования, проведенные в показали, что усреднен-ный тензор теплового расширения для шести возможных ОС отличается от вида secondary strains [18]. Поэтому, с учетом наличия спонтанных поворотов, возникает вопрос о корректности определения вида спонтанной деформации для фазового прехода . Из анализа получено, что все параметры решетки в сегнетоэластической фазе должны иметь нелинейную температурную зависимость, что соответствует экспериментальным результатам [20].

Таким образом, из условия сохранения макросимметрии можно определить усредненный тензор деформации полидоменного кристалла, а из вида тензора –какие параметры решетки будут иметь нелинейную температурную зависимость в сегнетоэластической фазе. При определении вида тензоров primary и secondary strains [18] необходимо учитывать наличие спонтанных поворотов при структурных фазовых переходах в сегнетоэластиках.

Литература:

1. Л.А. Шувалов, Кристаллография 8, 616 (1963).

2. K. Aizu, Phys. Rev. B. 2, 754 (1970).

3. Л.Г. Шабельников, В.Ш. Шехтман, О.М. Царев, ФТТ 18, 1529 (1976).

4. W.I.F. David, I.G. Wood, J. Phys. C: Solid State Phys 16, 5149 (1983).

5. В.А. Непочатенко, Кристаллография 50, 847 (2005).

6. L.A. Shuvalov, E.F. Dudnik, S.V. Vagin, Ferroelectrics 65, 143 (1985).

7. V.A. Nepochatenko, Ferroelectrics 359, 242 (2007).

8. В.А. Непочатенко, В.Г. Поздеев, Изв. РАН. Сер. физ. 77, 1115 (2013).

9. В.А. Непочатенко, Е.Ф. Дудник, ФТТ. 45, 1870 (2003).

10. V.A. Nepochatenko, Ferroelectrics, 341, 97 (2006).

11. В.А. Непочатенко, Изв. РАН. Сер. физ. 74, 1263 (2010).

12. Л.А. Шувалов, Изв. АН. СССР. Сер. физ. 43, 1554 (1979).

13. A.W. Sleight, H.Y. Chen, A. Ferretti, D.E. Cox, Mater. Res. Bull. 14, 1571 (1979).

14. W.I.F. David, A. M. Glazer, A.W. Hewat, Phase Transitions 1, 155 (1979).

15. В.А. Непочатенко, В.Т. Розумнюк, И. А. Непочатенко, Нано-и микросистемная техника. 5, 24 (2010).

16. J.Sapriel, Phys. Rev. B. 12, 5128 (1975).

17. В.А. Непочатенко, А.Ю. Кудзин, ФТТ. 48, 1071 (2006).

18. K. Aizu, Phys. Soc. Japan. 28,706 (1970).

19. W.I.F David. I.G. Wood, J. Phys. C: Solid State Phys. 16. 5127(1983).

20. Guimaraes D.M.C. Phase Transitions. 1. 143(1978).