УДК 622.02+532.5
К.ф-м.н. Танирбергенов А.Г., к.т.н. Нурбекова К.С.,
магистрант Ергалиев Б.
Казахский национальный технический университет им.
К.И. Сатпаева, Алматы, Казахстан
е-mail:
tan.amanjol@mail.ru
ЧИСЛЕННОЕ
ИССЛЕДОВАНИЕ ПРОЦЕССА ФОРМИРОВАНИЯ НЕФТЕГАЗОНОСНЫХ СОЛЯНЫХ КУПОЛОВ В ЗАВИСИМОСТИ ОТ ГЕОМЕТРИИ И РАЗМЕРА СОЛЯНОГО МАССИВА
Введение. В
земной коре распространены солянокупольные геологические структуры.
Возникновение этих структур геологи связывают с действием гравитационных
сил, когда первоначально пластообразно
залегавшие более легкие соляные породы
поднимаясь, внедрялись в
вышележащую толщу осадочных горных пород в виде соляных куполов (гравитационная
неустойчивость). Такой процесс
называется течением; он настолько медленный, что заметно проявляется
только в геологическом масштабе времени
[1, 2]. В природных условиях соль - твердое кристаллическое тело, под длительной постоянной нагрузкой ведет
себя как очень вязкая несжимаемая жидкость и деформируется без разрушения. Для
исследования движения соляного купола, обычно, используется модель неоднородной сильновязкой несжимаемой
жидкости. Процесс возникновения и роста соляного купола условно можно разделить
на две стадии, линейную и нелинейную. На линейной стадии изучаются небольшие
деформации соли; эта стадия достаточно подробно изучена рядом авторов
аналитическими методами. Для исследования нелинейной стадии – стадии развитого
соляного купола – используются только численные методы.
Предшествующие работы, посвященные
численному анализу нелинейной стадии развития соляного купола, ограничены рассмотрением
небольших по размерам областей [5-6].
В связи с этим недостаточно изучено
влияние горизонтальных и вертикальных стенок области на рост и формы соляных
диапиров.
В данной работе в связи с ростом
мощности персональных компьютеров исследуются закономерности роста соляных диапиров
в относительно больших по размерам областях.
Постановка
задачи. Начально-краевая задача,
описывающая движение неоднородной сильновязкой
несжимаемой жидкости в поле силы тяжести в плоской постановке, формулируется следующим образом. В прямоугольной области W требуется
определить вектор скорости ![]() давление
давление ![]() плотность
плотность ![]() динамическую вязкость
динамическую вязкость
![]() в момент времени
в момент времени ![]() удовлетворяющих
системе уравнений
удовлетворяющих
системе уравнений
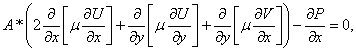 (1)
(1)
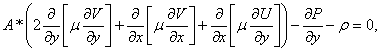 (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
![]() (5)
(5)
начальным и граничным условиям на
границе ¶W
![]() (6)
(6)
![]() (7)
(7)
![]() (8)
(8)
Система уравнений (1)–(5), начальные и
граничные условия (6)–(8) записаны в безразмерном виде. Здесь ![]() соответственно
горизонтальная и вертикальная составляющие скорости. Коэффициент
соответственно
горизонтальная и вертикальная составляющие скорости. Коэффициент ![]() равен отношению числа
Фруда к числу Рейнольдса,
равен отношению числа
Фруда к числу Рейнольдса, ![]() Здесь g – ускорение свободного падения,
Здесь g – ускорение свободного падения, ![]() характерные параметры среды, соответственно кинематическая вязкость, скорость и линейный размер области. В задачах гравитационной
неустойчивости отсутствует характерный масштаб скорости, поэтому в качестве
последнего в работе принимается вязкая
скорость
характерные параметры среды, соответственно кинематическая вязкость, скорость и линейный размер области. В задачах гравитационной
неустойчивости отсутствует характерный масштаб скорости, поэтому в качестве
последнего в работе принимается вязкая
скорость ![]() , где n – произвольное
число. Выбирая n определенным образом, получим
необходимый масштаб скорости рассматриваемой модели.
, где n – произвольное
число. Выбирая n определенным образом, получим
необходимый масштаб скорости рассматриваемой модели.
Численный
метод решения. Для численного решения
систем уравнений (1) –(3) используется итерационный процесс, основанный на
схеме расщепления по физическим процессам [3]. Пусть исследуемая область
течения Ω покрыта равномерной по x и y сеткой ячеек:
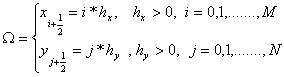
где
![]() размеры шагов сетки,
размеры шагов сетки, ![]() число ячеек сетки соответственно в направлениях x и y.
число ячеек сетки соответственно в направлениях x и y.
На первом этапе схемы расщепления по неявной схеме рассчитывается предварительное значение вектора
скорости:
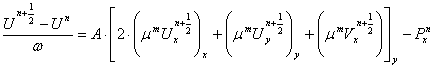 (9)
(9)
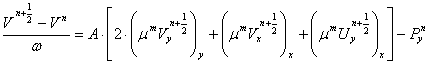 , (10)
, (10)
Уравнение
(9) рассматривается в точках сетки ![]() а уравнение (10) - в
точках
а уравнение (10) - в
точках ![]() . В уравнениях верхний индекс
. В уравнениях верхний индекс ![]() обозначает временной
слой, а
обозначает временной
слой, а ![]() номер итераций.
номер итераций.
На втором этапе по найденному промежуточному полю
скорости ![]() с учетом условия
соленоидальности вектора скорости
с учетом условия
соленоидальности вектора скорости ![]() находится поле
давления
находится поле
давления ![]() из уравнения:
из уравнения:
![]() . (11)
. (11)
Уравнение (11) рассчитывается в точках ![]()
На третьем
этапе находим ![]() из уравнений:
из уравнений:
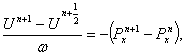 (12)
(12)
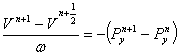 (13)
(13)
Уравнения
(12) и (13) рассматриваются соответственно в тех же точках, что (9) и (10).
Для численного решения уравнений (4),
(5) с начальными условиями (6), (7) соответственно, используется консервативная
схема разности против потока [4], при
этом шаг по времени ![]() выбирается с учетом устойчивости
и монотонности схемы:
выбирается с учетом устойчивости
и монотонности схемы:
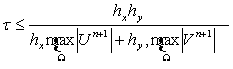 . (14)
. (14)
Для решения уравнений (9) – (11)
используется метод верхней релаксации. Как показали расчеты разностная схема (9)
– (13) абсолютно устойчива. Параметр ![]() выбирается с учетом
быстрой сходимости итерационного процесса.
выбирается с учетом
быстрой сходимости итерационного процесса.
Итак, предлагаемый алгоритм для
численного решения задачи (1)-(8)
выглядит следующим образом. Пусть ![]() известны (при
известны (при ![]() для
для ![]() и
и ![]() это будут начальные
данные ). Тогда неизвестные
это будут начальные
данные ). Тогда неизвестные ![]() определяются
итерационным процессом с повторением вышеуказанных трех этапов. При выполнении условия
определяются
итерационным процессом с повторением вышеуказанных трех этапов. При выполнении условия
![]()
итерационный процесс заканчивается. Это и означает,
что на ![]() - шаге по времени определены значения величин
- шаге по времени определены значения величин ![]() . Далее по явной схеме разности против потока вычисляются
неизвестные
. Далее по явной схеме разности против потока вычисляются
неизвестные ![]() на
на ![]() шаге по времени. Для нахождения
шаге по времени. Для нахождения ![]() опять применяется
итерационный процесс. Аналогично, определяются все величины
опять применяется
итерационный процесс. Аналогично, определяются все величины ![]() (
(![]() вплоть до необходимого
вплоть до необходимого
![]() слоя по времени.
слоя по времени.
Разностная
начально-краевая задача, соответствующая исходной задаче (1)-(8) записана в
дивергентной форме, что является необходимым и достаточным условием сходимости
разностного решения к точному. Численный метод пригоден при любых
распределениях вязкости и плотности, характерных для осадочного чехла, галита и
подсолевого ложа.
Анализ
результатов расчета. Для численного исследования неустойчивости соляного
массива рассмотрена модель двухслойной среды в случае, когда менее
плотный слой (соль) расположен под более плотным слоем (надсолевыми породами). В модели считается, что каждый слой
однороден по плотности и вязкости и различные слои могут быть разной мощности
(высоты), плотности и вязкости. Нумерация слоев принята сверху вниз. Параметры
каждого слоя записываются с нижним индексом, обозначающим его номер, например, ![]() соответственно
вязкость, плотность и мощность второго слоя, т. е. соли. Если в рассматриваемой
модели границы раздела слоев ровные, то в области сколь угодно долго
наблюдается неустойчивое равновесие. Это связано с тем, что горизонтальная
составляющая градиента давления в области равна нулю. Для куполообразования
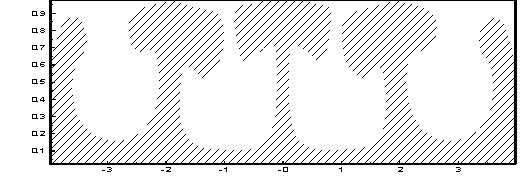
необходимы неровности на границах раздела слоев. На рисунках 1-3 представлена
эволюция границы раздела слоев для трех различных моделей, отличающихся друг от
друга только размерами области или то же самое - горизонтальными и
вертикальными размерами слоев. Размеры области и время развития гравитационной
неустойчивости приведены на рисунках в
безразмерном виде. Первоначальная
неровность во всех моделях задана в виде небольшого вздутия на границе раздела
слоев.
соответственно
вязкость, плотность и мощность второго слоя, т. е. соли. Если в рассматриваемой
модели границы раздела слоев ровные, то в области сколь угодно долго
наблюдается неустойчивое равновесие. Это связано с тем, что горизонтальная
составляющая градиента давления в области равна нулю. Для куполообразования
необходимы неровности на границах раздела слоев. На рисунках 1-3 представлена
эволюция границы раздела слоев для трех различных моделей, отличающихся друг от
друга только размерами области или то же самое - горизонтальными и
вертикальными размерами слоев. Размеры области и время развития гравитационной
неустойчивости приведены на рисунках в
безразмерном виде. Первоначальная
неровность во всех моделях задана в виде небольшого вздутия на границе раздела
слоев.
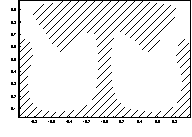
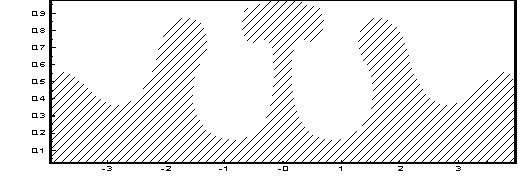
t=0 t=2.6
Рисунок 1 – Эволюция границы раздела слоев в процессе
гравитационной неустойчивости. Параметры
модели: ![]()
![]()
Из рисунков видно, что первичный соляной купол
формируется из первоначального возмущения,
вследствие оттока в него соли из материнского пласта. При этом в пласте
вокруг первичного купола образуются прогибы (компенсационные впадины), из
которых в дальнейшем образуются вторичные купола (рис. 1). Вследствие оттока
соли из пласта в эти вторичные купола,
вокруг них образуются вторичные прогибы. В дальнейшем из них формируются
третичные купола (рис.2). В зависимости от горизонтальных размеров соляного
пласта таких куполов в природных условиях может быть несколько десятков.
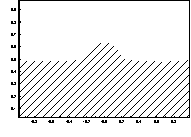
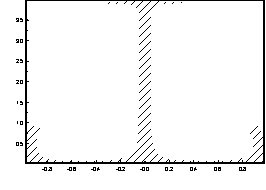
t=0.0
t=1.6
t=2.2
Рисунок 2 – Эволюция границы раздела слоев в процессе
гравитационной неустойчивости.
Параметры модели: ![]()
![]()
Все они принадлежат к одному семейству, так как они
своими появлениями обязаны первичному куполу.
Из сравнения рис. 1 и 2 видно, что на
образование вторичных куполов на рис. 1 кроме прогибов повлияла также и
близость вертикальных стенок области, тогда как вторичные купола на рисунке 2
формируются только из-за зарождения прогибов.
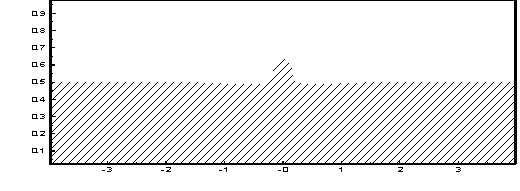
На рис. 1 и 3 представлена эволюция
границы раздела слоев для моделей,
отличающиеся только мощностями надсолевых пород или то же самое - расстоянием
между куполом и верхней горизонтальной стенкой. Из рисунков видно, что с увеличением мощности надсолевых пород
соляные купола приобретают столбообразную
форму, т. е. везде почти одинаковой ширины. Именно такие купола называют
диапирами, т. е. купола протыкающего типа (рис. 3). При приблизительно равной мощности слоев верхняя часть купола
расширяется, и купол, не достигая
верхней стенки, приобретает
грибовидную форму (рис. 1).
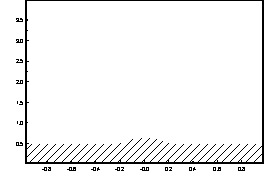
t=0 t=1.5
Рисунок 3 – Эволюция границы раздела слоев в процессе
гравитационной неустойчивости.
Параметры модели: ![]()
![]()
Литература
1.
Косыгин Ю.А. 1995. Основы тектоники нефтеносных областей. М.: Гостоптехиздат, 511с.
2.
Рамберг Х. 1985. Сила тяжести и деформаций в земной коре. Пер. с англ. –М.:
Недра, 400с.
3..
Белоцерковский О.М. 1984. Численное моделирование в механике сплошных сред. М.:
Наука, 520c.
4.
Роуч Х. 1980. Вычислительная гидродинамика. М.: Мир, 616с.
5. Woid W.D., Neugebauer H.J.
1980. Finite element models of density instabilities by means of bicubic spline
interpolation.-Phys. Earth Planet. Inter.,
v. 21, p. 176-180.
6.
Zaleski
S., Julien P. 1992. Numerical simulation of Rayliegh-Taylor instability for
single and multiple salt diapirs // Tectonophysics, V. 206, p. 55-69.
7. Орунханов М.К., Танирбергенов А.Г. 2000.
Численное моделирование процесса формирования нефтяных соляных куполов. //
Нефть и газ, №2, 25-37c.