УДК 622.02+532.5
К.ф.-м.н. А.Г.Танирбергенов, магистрант Ергалиев,
магистрант Мураткажин Д, магистрант Карабалиев Е.Н.
Казахский национальный технический университет им.
К.И. Сатпаева
Алматы,
Казахстан е-mail: tan.amanjol@mail.ru
ЧИСЛЕННЫЙ МЕТОД В ПЕРЕМЕННЫХ ФУНКЦИЯ ТОКА – ВИХРЬ ДЛЯ
ИССЛЕДОВАНИЯ ЗАДАЧИ О ГРАВИТАЦИОННОЙ
НЕУСТОЙЧИВОСТИ СИЛЬНОВЯЗКОЙ НЕСЖИМАЕМОЙ ЖИДКОСТИ
Введение.
Многие медленные технологические и природные
процессы изучаются на модельных уравнениях гидродинамики неоднородной вязкой
несжимаемой жидкости. Среди подобных
исследований особое место занимает задача изучения ползущих движений
в поле силы тяжести. К ним относятся задача изучения условий
формирования солянокупольных структур и мантийных диапиров в земной коре,
которое имеет большое научное и практическое значение, поскольку с последними
связано распределение нефти и газа, а также полезных ископаемых в земной коре. Возникновение этих структур геологи связывают
с действием гравитационных сил, когда
первоначально пластообразно залегавшие более легкие соляные породы поднимаясь,
внедрялись в вышележащую толщу осадочных горных пород в виде соляных
куполов (гравитационная неустойчивость).
Такой процесс называется течением; он настолько медленный, что заметно
проявляется только в геологическом
масштабе времени [1, 2]. В природных условиях соль - твердое
кристаллическое тело, под длительной
постоянной нагрузкой ведет себя как очень вязкая несжимаемая жидкость и
деформируется без разрушения. Для исследования движения соляного купола,
обычно, используется модель
неоднородной сильновязкой несжимаемой жидкости. Процесс возникновения и роста
соляного купола условно можно разделить на две стадии, линейную и нелинейную.
На линейной стадии изучаются небольшие деформации соли; эта стадия достаточно
подробно изучена рядом авторов аналитическими методами. Для исследования
нелинейной стадии – стадии развитого соляного купола – используются только
численные методы. Работы в этом направлении немногочисленны и они
ограничены в основном рассмотрением
численных методов в переменных скорость – давление [6-8].
В
данной работе для исследования гравитационной неустойчивости сильновязкой
жидкости предлагается численный метод в переменных функция тока – вихрь.
Постановка
задачи. Начально-краевая задача,
описывающая движение неоднородной сильновязкой
несжимаемой жидкости в поле силы тяжести в плоской постановке, формулируется следующим образом. В прямоугольной области W требуется
определить вектор скорости ![]() давление
давление ![]() плотность
плотность ![]() в момент времени
в момент времени ![]() удовлетворяющих
системе уравнений
удовлетворяющих
системе уравнений
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
начальным и граничным условиям на
границе ¶W
![]() (5)
(5)
![]() (6)
(6)
Здесь
![]() - динамическая
вязкость среды,
- динамическая
вязкость среды, ![]() соответственно
горизонтальная и вертикальная составляющие скорости. По приведенным ниже
формулам
соответственно
горизонтальная и вертикальная составляющие скорости. По приведенным ниже
формулам
![]() ,
, ![]() , (7)
, (7)
![]() (8)
(8)
введем соответственно функцию тока ![]() и вихрь
и вихрь ![]() . Дифференцируя уравнение
(1) по
. Дифференцируя уравнение
(1) по ![]() , уравнение (2) по
, уравнение (2) по ![]() и, вычитая
из уравнения (1) уравнение (2) с учетом (7), (8) получим вместо системы
уравнений (1)-(3) равносильную ей систему уравнений в переменных функция тока и
вихрь
и, вычитая
из уравнения (1) уравнение (2) с учетом (7), (8) получим вместо системы
уравнений (1)-(3) равносильную ей систему уравнений в переменных функция тока и
вихрь
![]() (9)
(9)
![]() (10)
(10)
Запишем уравнения (9), (10), (4), начальное и граничное условия (5), (6) в
безразмерном виде с помощью следующих обозначений
![]()
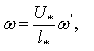
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,
![]() ,
, ![]()
![]() (11)
(11)
и для простоты записи опустив штрихи в безразмерных переменных:
![]() (12)
(12)
![]() , (13)
, (13)
![]() (14)
(14)
![]() (15)
(15)
![]() (16)
(16)
Коэффициент
![]() равен отношению числа
Рейнольдса к числу Фруда,
равен отношению числа
Рейнольдса к числу Фруда, ![]() Здесь
Здесь ![]() – ускорение
свободного падения,
– ускорение
свободного падения, ![]() характерные параметры среды, соответственно плотность, кинематическая вязкость, скорость и
линейный размер области. В задачах
гравитационной неустойчивости отсутствует характерный масштаб скорости, поэтому
в качестве последнего в работе
принимается вязкая скорость
характерные параметры среды, соответственно плотность, кинематическая вязкость, скорость и
линейный размер области. В задачах
гравитационной неустойчивости отсутствует характерный масштаб скорости, поэтому
в качестве последнего в работе
принимается вязкая скорость ![]() , где n – произвольное
число. Выбирая n определенным образом, получим
необходимый масштаб скорости рассматриваемой модели.
, где n – произвольное
число. Выбирая n определенным образом, получим
необходимый масштаб скорости рассматриваемой модели.
Численный
метод решения. Пусть исследуемая
область течения Ω покрыта равномерной по x и y сеткой ячеек:
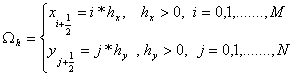
где
![]() размеры шагов сетки,
размеры шагов сетки, ![]() число ячеек сетки соответственно в направлениях x и y [4]. Для численного решения уравнений (12), (13)
рассмотрим конечно-разностную схему [5]:
число ячеек сетки соответственно в направлениях x и y [4]. Для численного решения уравнений (12), (13)
рассмотрим конечно-разностную схему [5]:
![]() (17)
(17)
![]() (18)
(18)
Уравнения
(17), (18) рассматриваются в точках ![]() разнесенной сетки
разнесенной сетки ![]() . Здесь
. Здесь ![]() итерационный
параметр. В уравнениях верхний индекс
итерационный
параметр. В уравнениях верхний индекс ![]() обозначает временной
слой, а
обозначает временной
слой, а ![]() номер итераций.
Граничные условия для функции тока имеют вид
номер итераций.
Граничные условия для функции тока имеют вид
![]() ,
, 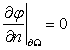 . (19)
. (19)
Это
следует из условий (16). Граничные условия для вихря получатся из уравнения (18) при рассмотрении его на
границе и аппроксимации функции тока в приграничных точках, и учета условий (19)
[5]. Например, для границы ![]() имеем
имеем
![]() . (20)
. (20)
Для численного решения уравнений (17),
(18) с граничными условиями соответственно (20), (19) используется метод верхней релаксации.
Для численного решения уравнения (14) используется
консервативная схема разности против потока [6], которая записывается
следующим образом:
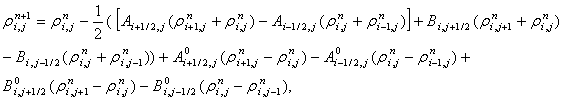
(21)
![]()
где 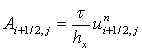 ,
, ![]() ,
,
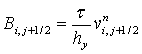 ,
, ![]() .
.
Шаг по времени ![]() выбирается с учетом
устойчивости и монотонности схемы:
выбирается с учетом
устойчивости и монотонности схемы:
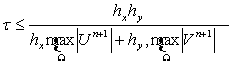 . (22)
. (22)
Итак, алгоритм решения разностной
задачи (17) – (21) следующий.
1.
Совместно решаются уравнения (17), (18) вплоть до установления итерационного
процесса, т.е. пока 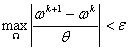 . Это означает, что на n – временном слое найдены значения функции тока и
вихря, т.е.
. Это означает, что на n – временном слое найдены значения функции тока и
вихря, т.е. ![]() и
и ![]() .
.
2.
Численным дифференцированием определяются значения скоростей по формулам
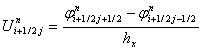 ,
, 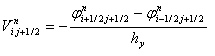
3.
Из уравнения (21) явным образом находим
![]() с учетом условия
устойчивости и монотонности схемы.
с учетом условия
устойчивости и монотонности схемы.
Аналогично, определяются все величины ![]() (
(![]() вплоть до необходимого
вплоть до необходимого
![]() слоя по времени. Рассмотренный численный метод пригоден при
любых распределениях вязкости и плотности, характерных для осадочного чехла в
природных условиях.
слоя по времени. Рассмотренный численный метод пригоден при
любых распределениях вязкости и плотности, характерных для осадочного чехла в
природных условиях.
Обсуждение
результатов расчета. Для численного исследования гравитационной
неустойчивости соляного массива рассмотрена модель двухслойной среды, в
случае, когда менее плотный слой (соль)
расположен под более плотным слоем (надсолевыми породами). В модели считается,
что каждый слой однороден по плотности и различные слои могут быть разной
мощности (высоты), плотности. Нумерация слоев принята сверху вниз. Параметры
каждого слоя записываются с нижним индексом, обозначающим его номер, например, ![]() соответственно,
плотность и мощность второго слоя,
т. е. соли. Вязкость во всей двухслойной среде одинакова и равна
соответственно,
плотность и мощность второго слоя,
т. е. соли. Вязкость во всей двухслойной среде одинакова и равна ![]() Если в рассматриваемой модели границы раздела слоев ровные,
то в области сколь угодно долго наблюдается неустойчивое равновесие. Это
связано с тем, что горизонтальная составляющая градиента давления в области
равна нулю. Для куполообразования необходимы неровности на границах раздела
слоев. Разработанным выше численным методом был проведен расчет указанной численной модели. На рисунках 1а - е показана эволюция границы раздела слоев в
процессе неустойчивости. Первоначальная неровность в виде небольшого вздутия
представлена на рис. 1 а.
Размеры области и время развития гравитационной неустойчивости приведены на рисунках в безразмерном виде.
Если в рассматриваемой модели границы раздела слоев ровные,
то в области сколь угодно долго наблюдается неустойчивое равновесие. Это
связано с тем, что горизонтальная составляющая градиента давления в области
равна нулю. Для куполообразования необходимы неровности на границах раздела
слоев. Разработанным выше численным методом был проведен расчет указанной численной модели. На рисунках 1а - е показана эволюция границы раздела слоев в
процессе неустойчивости. Первоначальная неровность в виде небольшого вздутия
представлена на рис. 1 а.
Размеры области и время развития гравитационной неустойчивости приведены на рисунках в безразмерном виде.
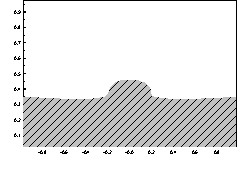

a) t=0.0 б) t=0.5


в) t=0.8 г) t=1.2


д) t=1.6 е) t= 2.0
Рисунок 1а-е – Эволюция границы
раздела слоев в процессе гравитационной неустойчивости. Параметры модели: ![]()
![]()
Из рисунков видно, что со временем из заданного первоначального возмущения формируется
соляной купол путем оттока соли из основного материнского пласта в этот купол.
И, наоборот, тяжелый надсолевой слой опускается вниз, выталкивая при этом соляной
массив наверх. Происходит перераспределение масс. Видно также образование на
краю прогибов вторичных куполов, которые
наклонены в сторону первичного купола. Это связано с тем, что на
вертикальных границах области (как и везде) заданы условия жесткого сцепления
(16).
Следует отметить, что аналогичные
результаты получены автором ранее с помощью численного метода в переменных
скорость – давление [8]. Преимуществом вышеуказанного численного метода в переменных функция тока – вихрь является простота
использования и быстрая сходимость итерационного процесса, т.е. экономия
машинного времени. Это преимущество особенно
существенно, когда исследуется гравитационная неустойчивость в
больших по размеру областях.
Список литературы
1.
Косыгин Ю.А. Основы тектоники нефтеносных областей. М.: Гостоптехиздат, 1952, 511с.
2. Рамберг Х. Сила тяжести и деформаций в
земной коре. Пер. с англ. –М.: Недра, 1985, 400с.
3. Белоцерковский О.М. Численное моделирование
в механике сплошных сред. М.: Наука, 1984, 520c.
4. Роуч Х. Вычислительная гидродинамика. М.:
Мир, 1980, 616с.
5. Пасконов В.М., Полежаев В.И., Чудов Л.А.
Численное моделирование процессов тепло- и массообмена - М: Наука, 1984, 288с.
6 Woid W.D., Neugebauer H.J. Finite element models of density
instabilities by means of bicubic spline interpolation.-Phys. Earth Planet.
Inter., 1980, v. 21, p. 176-180.
7 Zaleski S., Julien P.
Numerical simulation of Rayliegh-Taylor instability for single and multiple
salt diapirs // Tectonophysics. 1992. V. 206. p. 55-69.
8. Орунханов М.К., Танирбергенов А.Г.
Численное моделирование процесса формирования нефтяных соляных куполов. //
Нефть и газ, 2000, №2, с. 25-37.