Технические науки/12.Автоматизированные системы управления на производстве

Ладієва Л. Р., Олійник В. В.

Національний технічний університет України «КПІ»

СТАТИЧНА ОПТИМІЗАЦІЯ ПРОЦЕСУ ОЧИЩЕННЯ ОЦТОВОЇ КИСЛОТИ В РЕАКТОРІ З МІШАЛКОЮ

Успішне рішення задачі статичної оптимізації підсистем виробництва оцтової кислоти окисленням ацетальдегіду та координації їх узгодженої роботи дає змогу використати методи оптимізації для зменшення розмірності загальної оптимізаційної задачі та потрібного для її вирішення часу роботи ЕОМ і забезпечити економію обчислювальних ресурсів та їх надійність.

Дуже важливою для отримання оцтової кислоти високої якості є стадія очищення оцтової кислоти в реакторі з мішалкою.

Тому буде розроблена статична модель роботи реактора з мішалкою по очищенню оцтової кислоти. Сам процес не є важким і не представляє великих труднощів, але ж необхідність в технологічному процесі є.

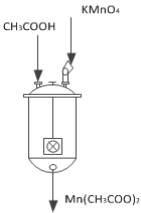
Рис. 1. Реактор з мішалкою

В реактор з мішалкою (див. рисунок 1) подається оцтова кислота CH₃COOH, яку потрібно очистити від домішок і перманганат калію KMnO_4. За допомогою лопатевої мішалки ці два компоненти змішуються і на виході утворюється ацетат марганцю Mn(CH₃COO)₂

Об¢єкт дослідження: реактор з мішалкою в якому відбувається очищення оцтової кислоти.

Щоб сформулювати критерій оптимальності (див. рисунок 2)для задачі статичної оптимізації оберемо квадратичний критерій, бо дана модель лінійна:

Нам необхідно підтримувати на певному рівні концентрацію ацетату марганцю на виході реактора з мішалкою. Тобто в критерій оптимальності включаємо концентрацію речовини в реакторі:

Сформулюємо основне рівняння статики для рідини:

G_вх1C_вх1+G_вх2C_вх2–G_вихC_вих–V_rw=0

В даному апараті ми не можемо змінювати витрату перманганату калію у будь-якому діапазоні. Тому в ньому ця витрата має бути в межах від 0.01 до 0.03 кг/с.

G_{вх2 min}<G_вх2<G_{вх2 max}

0.1<Gвх₂<0.3

Маючи статичну модель, критерій оптимальності і обмеження перетворимо задачу умовної оптимізації в безумовну.

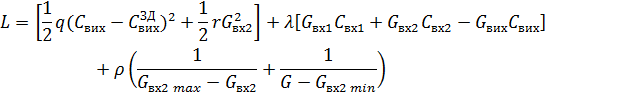
Необхідними умовами оптимальності будуть

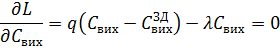
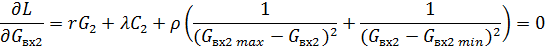
Запишемо алгоритм розрахунку з використанням градієнтної процедури:

1. Задаємо значення ;

2. Розв’язуємо математичну модель. Знаходимо ;

3. Розв’язуємо ;

4. Знаходимо ;

5. Розраховуємо оптимальне значення керування .

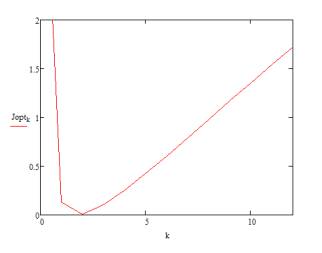
Рис. 2. Критерій оптимальності

Література:

1. Юкельсон И. И. Технология основного органического синтеза [Текст] / И.И. Юкельсон. – М.: «Химия», 1968 – 848 с.: ил. – Библиогр.: с. 401 – 408. – 30000 экз.

2. Анисимов И. В. Автоматическое регулирование процесса ректификации [Текст]/ И. В. Анисимов. – М.: «Гостоптехиздат», 1961. – 179 с.: ил. – Библиогр.: с. 6–20. – 3275 экз.