Расчет теплового сопротивления полупроводниковых источников света

С.А. Бакланов, Д.Е. Вагин, студенты группы 313-М

Научный руководитель С.В. Смирнов, проф., д.т.н

г.Томск, ТУСУР, grey-foton@list.ru

Важной особенностью полупроводниковых источников света является то, что они, в отличие от традиционных ламп, через 50–100 тысяч часов не выходят из строя. Наблюдается лишь постепенное снижение их светового потока. Одной из причин уменьшения светового потока является деградация некоторых частей источника света (самого полупроводникового кристалла и люминофора, если он используется) под действием температуры. Если отвод тепла от кристалла невысок, то с ростом температуры будут ухудшаться характеристики источника вплоть до выхода его из строя. Параметр, характеризующий способность источника света (ИС) препятствовать отводу тепла, называется тепловым сопротивлением. Чем выше тепловое сопротивление, тем хуже происходит теплоотвод, и тем быстрее ИС выйдет из строя. Поэтому расчет теплового сопротивления актуален в плане разработки и улучшения ИС.

Расчет теплового сопротивления основывается на следующих положениях. При протекании тока через осветительное устройство, оно нагревается, что влияет на многие его параметры и характеристики. На рисунке 1 показано изменение длины волны осветительного устройства от температуры окружающей среды [1]. Как можно заметить, изменение это линейно. Таким образом, можно сделать вывод о существовании возможности расчета температуры p-n перехода рабочего кристалла через измерение изменения длины волны испускаемого им света.

Для улучшения качества измерения вместо изменения максимума спектра излучения под действием температуры было использовано изменение полуширины спектральной линии [2].

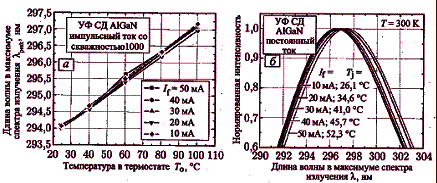
Рисунок 1 – Зависимость длины волны в максимуме спектра излучения от температуры в термостате для светодиода AlGaN УФ диапазона свечения в импульсном режиме со скважистостью 1000 (а). Спектры излучения и температуры переходов при разных значениях постоянного тока (б).

Учитывая, что при достаточно малом времени импульса тока, поданного на ИС, кристалл нагреться не успеет, то прямые зависимости полуширины от температуры при подаче на ИС импульсного и прямого токов будут отличаться. Используя данное отличие, можно найти тепловое сопротивление ИС по следующей формуле:

(1)

где - тепловое сопротивление, град/Ватт;

- температура кристалла ИС при нагреве его прямым током, °С;

Т_имп – температура кристалла ИС при подаче на него импульсного тока, °С. Равна температуре окружающей среды, при которой проводились измерения.

На рисунке 2 представлены зависимости полуширины спектра ИС от температуры при подаче на него импульсного и прямого токов. Источниками света выступали 2 светодиодные лампы красного спектра излучения с одним кристаллом в корпусе S6s. Измерение спектра проводилось спектрометром USB2000 фирмы Ocean Optics.

Как можно заметить из рисунка 2, зависимости полуширины от температуры действительно линейные, что доказывается линиями тренда с высокими коэффициентами достоверности аппроксимации. Из данных зависимостей были рассчитаны соответствующие тепловые сопротивления – 111,24 град/Ватт для ИС (а) и 104,77 град/ Ватт для ИС (б).

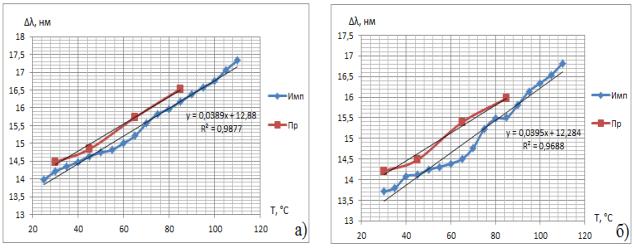
Рисунок 2 - Зависимости полуширины спектра ИС от температуры при подаче на него импульсного и прямого токов для двух источников красного света

Полученные значения весьма правдоподобны, что доказывает применимость данного метода получения значения теплового сопротивления на практике.

Список использованной литературы.

1. Шуберт Ф. Светодиоды. - М.: Физматлит, 2008. - 496 с.

Смирнов С.В., Саврук Е.В., Гончарова Ю.С.; заявитель и патентообладатель Томский гос. университет систем управления и радиоэлектроники. - № 2538070; заявл. 18.07.2013; опубл. 10.01.2015, - 2 стр.