Сатыбалдиев
О.С. п.ғ.д., Акимжанова Ш.А. аға оқытушысы
Математикалық модельдердің көмегі
арқылы жылу өткізгіштік теңдеуінің шешімін табу
Математикалық
модельдер сонау Ф.Кенэ, А.Смит, Д.Рикардо
өмір сүрген заманнан объектілерді зерттеу және оларды
белгілі бір заңдылықтар бойынша сипаттау мақсатында
қолданылып келеді. Алдымен математикалық модель деген не?
Оның негізгі элементтері неден тұрады? деген секілді
сауалдардың төңірегінде әңгіме
қозғалық.Қандайда бір объектінің
математикалық моделі деп, біз, теңдеулердің,
теңсіздіктердің, логикалық қатынастардың
және графиктердің гомоморфтық бейнелеуін түсінеміз.
Гомоморфтық бейнелеу зерттелініп отырған объектінің
элементтері мен модель элементтерінің аралығындағы
қатынастарды біріктіреді. Басқаша айтқанда модель объектіні
қысқа мерзім аралығында зерттеу үшін
құрылған шартты бейне. Модельді зерттеу арқылы біз
объект туралы жаңа мәліметтер аламыз. Сонымен қатар,
модельдер қай жағдайда қандай шешімді қабылдауға
мүмкіндік береді.
Математикалық модельдердің негізгі элементтері туралы
түсініктерді нақтылау үшін техника саласындағы
төмендегі есепті қарастыралық және оның
математикалық модельдерін құралық.
Есеп. Шеттеріндегі температуралары
тұрақты, ал бастапқы температурасы белгілі болған жағдайдағы стержендегі
жылудың таралу заңдылығын ізделік.
![]() , (1)
, (1)
теңдеуі стержендегі жылудың таралу
теңдеуі немесе жылу өткізгіштік теңдеуі деп
аталатыны белгілі.
Енді
жоғарыдағы есептің математикалық моделін
құралық.
![]() облысында
облысында
![]() , (2)
, (2)
шекаралық шартын және
![]() , (3)
, (3)
бастапқы шартын
қанағаттандыратын (1) теңдеудің шешімін
табу қажет болсын. (2) шарт стерженнің ![]() және
және ![]() шеттеріндегі
сәйкес температуралары
шеттеріндегі
сәйкес температуралары ![]() мен
мен ![]() тұрақты
екендігін, ал стерженнің бастапқы температурасы
тұрақты
екендігін, ал стерженнің бастапқы температурасы ![]() функциясы
арқылы өрнектелетіндігін көрсетеді.
функциясы
арқылы өрнектелетіндігін көрсетеді.
Көп жағдайда (1) – (3) есебінің шешімін
(2) біртекті шекаралық шарттар бойынша айнымалыларды болу әдісі
қолданылады. Біз осы әдісті біртектес емес шекаралық шарттар
жағдайына пайдаланамыз.
(1)
теңдеудің нөлден өзгеше және (2) шекаралық
шартты қанағаттандыратын шешімін
![]() (4)
(4)
түрінде ізделік. (1) теңдеуден
![]() ,
,
немесе
![]() (5)
(5)
теңдіктерін аламыз. (5)
теңдіктің сол жағы тек қана ![]() ке, ал оң жағы тек қана
ке, ал оң жағы тек қана ![]() ға тәуелді, яғни
ға тәуелді, яғни ![]() . Мұндай теңдік тек қана
. Мұндай теңдік тек қана ![]() жағдайда
орындалады. Олай болса
жағдайда
орындалады. Олай болса
![]() , (6)
, (6)
мұндағы ![]() тұрақты
шама, ал теріс таңба ыңғайлы болу үшін алынды. Сонымен,
(1) дербес туындылы дифференциалдық теңдеуді айнымалыларды
бөлу әдісінің көмегі арқылы
тұрақты
шама, ал теріс таңба ыңғайлы болу үшін алынды. Сонымен,
(1) дербес туындылы дифференциалдық теңдеуді айнымалыларды
бөлу әдісінің көмегі арқылы
![]() , (7)
, (7)
![]() (8)
(8)
екі қарапайым дифференциалдық
теңдеулерге алып келдік.
Енді
![]() параметрін
анықтау мәселесін қарастыралық. (7) мен (8)
теңдеулерінің шешімдері сәйкес
параметрін
анықтау мәселесін қарастыралық. (7) мен (8)
теңдеулерінің шешімдері сәйкес
![]() , (9)
, (9)
![]() . (10)
. (10)
болады. Алайда (9) жалпы шешім (7)
теңдеудің ![]() болған
жағдайдағы шешімі болады. Ал
болған
жағдайдағы шешімі болады. Ал ![]() болса
болса ![]() теңдеуін
аламыз. Бұл теңдеудің жалпы шешімі
теңдеуін
аламыз. Бұл теңдеудің жалпы шешімі ![]() болады. Демек, (9)
теңдеудің жалпы шешімі
болады. Демек, (9)
теңдеудің жалпы шешімі
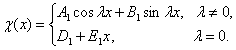
түрінде жазылады. Дәл
осылай пайымдай отырып (8) теңдеудің жалпы шешімін
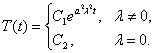
түрінде жазамыз. Сонымен, (1) теңдеудің
![]()
![]()
және
![]() .
.
екі шешімі бар екен.
Мұндағы ![]() тұрақты сандар. Жаңа белгілеулер енгізіп
тұрақты сандар. Жаңа белгілеулер енгізіп
![]() , (11)
, (11)
![]() . (12)
. (12)
түрінде жазамыз. (1) теңдеу
сызықтық теңдеу, олай болса (11) пен (12) дербес
шешімдердің қосындысында осы теңдеудің шешімі, болады
яғни
![]() ,
(13)
,
(13)
Мұндағы ![]() кезкелген
тұрақтылар. Бұл тұрақтыларды (2) шекаралық
шарт пен (3) бастапқы шарт орындалатындай етіп таңдаймыз.
Стерженнің сол жақ шетіндегі шекаралық шарттан басталық
кезкелген
тұрақтылар. Бұл тұрақтыларды (2) шекаралық
шарт пен (3) бастапқы шарт орындалатындай етіп таңдаймыз.
Стерженнің сол жақ шетіндегі шекаралық шарттан басталық
![]() .
.
Осыдан
![]() .
.
1 және ![]() функциялары
функциялары ![]() аралығында
сызықты тәуелсіз болғандықтан соңғы
теңдіктен
аралығында
сызықты тәуелсіз болғандықтан соңғы
теңдіктен
![]()
теңдігін аламыз. ![]() мен
мен ![]() - ның мәндерін (13) теңдікке
қойып
- ның мәндерін (13) теңдікке
қойып
![]() (14)
(14)
теңдігін
аламыз. Стерженнің оң шетіндегі шекаралық шартты пайдаланып
![]()
және
![]() ,
,
теңдіктерін аламыз. Жоғарыдағыдай 1 мен ![]() функцияларының сызықты
тәуелсіздіктеріне сәйкес
функцияларының сызықты
тәуелсіздіктеріне сәйкес
![]() , (15)
, (15)
![]() (16)
(16)
теңдіктерін
аламыз. (15) теңдіктен
![]() .
.
(16) теңдік ![]() және
және ![]() теңдіктеріне
немесе
теңдіктеріне
немесе ![]() теңдігіне
көшеді. Егер
теңдігіне
көшеді. Егер ![]() болса, онда (18)
теңдіктен
болса, онда (18)
теңдіктен ![]() көбейткішін
жоғалтамыз да
көбейткішін
жоғалтамыз да
![]() ,
,
шешімін
аламыз. Бұл шешім (4) бастапқы шартын қанағаттандырады,
яғни
![]() .
.
Осы арада мынандай қатаң шартқа кезігіміз:
стерженнің бастапқы температурасы тек сызықтық функция
арқылы өрнектелуі қажет. Мұндай қатаң шарт,
әрине, ыңғайсыздық тудырады. Сондықтан ![]() деп
ұйғара отырып
деп
ұйғара отырып
![]() (17)
(17)
жағдайын
таңдаймыз. (17) теңдеудің шешімі
![]() (18)
(18)
болады. Соңғы теңдіктегі ![]() мәнін алып
тастаймыз, себебі
мәнін алып
тастаймыз, себебі ![]() болса, онда
болса, онда ![]() болады. Сол секілді
болады. Сол секілді ![]() - ның теріс
мәндерін алып тастауға болады.
- ның теріс
мәндерін алып тастауға болады.
(13) теңдікке суперпозиция
қағидасын қолданып
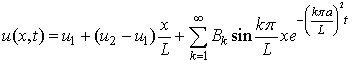 (19)
(19)
теңдігін аламыз. Осы (19) қатар арқылы берілген ![]() функциясы (2)
шекаралық шартты қанағаттандырады. Шынында да
функциясы (2)
шекаралық шартты қанағаттандырады. Шынында да ![]() , себебі
, себебі ![]() болғанда
болғанда ![]() және
және ![]() болғанда
болғанда ![]() .
.
Пайдаланылған
әдебиеттер
1. Яглом И.М.
Математические структуры и математическое моделирование. – М., Наука, 2010. -
327с.
2. Хатсон В., Пим Дж.
Приложения функционального анализа и теории операторов.- М., Мир, 2012. - 357с.
3. Гусейнзаде М.А. и др.
Применение обобщенных функций в задачах трубопроводного транспорта нефти и
газа. – М.: РГУ нефти и газа им. И.М. Губкина, 2011. - 415с.