Доповідь/Технічні науки – Автоматизовані системи управління на виробництві

УДК 681.5

Зварич З.М.

Івано-Франківський національний технічний університет нафти і газу

Оптимізація параметрів цифрових fuzzy-регуляторів

Застосування нечіткого регулятора (НР) для керування різними об`єктами показує їх високу ефективність і в ряді випадків суттєві переваги перед лінійними цифровими регуляторами [1,2]. Основними параметрами цифрових НР, при яких відбувається їх синтез і розрахунок, є, кількість і форма функцій належності (ФН) лінгвістичних величин і діапазони зміни вхідних і вихідної лінгвістичних змінних помилка системи θ, перша похідна помилки , друга похідна помилки , керуючий вплив на об'єкт m, тобто [θ_min , θ_max], [_{min , max}] і [m_min , m_max].

Вибір ФН при синтезі НР для систем автоматичного керування (САК) має специфічні особливості, які обумовленні тим, що на вхід НР, як правило, поступають три лінгвістичні змінні: помилка системи θ, швидкість зміни (перша похідна) помилки , прискорення(друга похідна) помилки , які якісно можна охарактеризувати (за допомогою спрощення розрахунків), наприклад негативна -1, позитивна – 2.

Ці терм-множини описуються на універсальній множині U відповідно двома ФН: і . ФН визначає степінь належності кожного елементу u множині U числом між 0 і 1, яке називають степенем істинності даної лінгвістичної змінної даному терму. Тому функції і повинні бути симетричними одна відносно одної і перетинатися при u = 0,5. крім того, функція повинна бути спадаючою, а - зростаючою.

Із врахуванням вищесказаного можна записати наступні аналітичні вирази, які часто використовуються на практиці ФН для вхідних лінгвістичних змінних при проектуванні цифрових НР САК:

· для трикутних ФН:

= u / c, 0 ≤ u ≤ c;

= (1- c - u) / (1- 2c), c ≤ u ≤ 1 – c;

= 0, 1 – c ≤ u ≤ 1;

= 0, 0 ≤ u ≤ c; (1)

= (u - c) / (1- 2c), c ≤ u ≤ 1 – c;

= (1- u) / c, 1- c ≤ u ≤ 1;

· для трапецеєвидних ФН:

= 1, 0 ≤ u ≤ c;

= (1- c - u) / (1- 2c), c ≤ u ≤ 1 – c;

= 0, 1 – c ≤ u ≤ 1;

= 0, 0 ≤ u ≤ c; (2)

= (u - c) / (1- 2c), c ≤ u ≤ 1 – c;

= 1, 1 – c ≤ u ≤ 1;

(у формулах (1) і (2) параметром с можна варіювати в межах 0 ≤ с ≤ 0,49;

При с = 0 = (1- u), = u, 0 ≤ u ≤ 1;

· для піднесених в степінь трикутних ФН:

= (1- u)^с, = u^с. (3)

· для дзвоноподібних ФН:

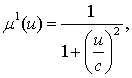
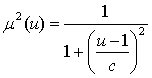. (4)

· для гаусових ФН

, . (5)

· для експоненціальних ФН:

, (6)

ФН, які аналітично визначаються формулами (3)- (6), мають лише один параметр – коефіцієнт с, яким можна варіювати при налаштуванні НР, що влаштовує з практичної точки зору.

Для вихідної лінгвістичної змінної - керуючого впливу на ОК m можна використовувати такі ж ФН, як і для вхідних лінгвістичних змінних.

Як приклад на рис.1 показані експоненціальні ФН на універсальній множині і діапазони змінних, а також результуюча ФН (жирна лінія) для конкретних змінних.

Результуюючу ФН отримують як правило «мінімаксним» методом, а розрахунок абсциси "центру тяжіння" s_c=S(u_c , µ_c) ділянки площі, що охоплена результуючою ФН μ(u) в межах зміни змінної u від u = U₁ до u = U₂, зручно виконувати, використовуючи чисельне інтегрування за методом трапецій (з кроком дискретизації u₀), за формулою:

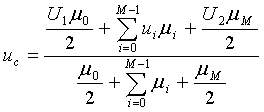, (7)

де (U₂ –U₁) / M = u₀ - крок дискретизації, М- число дискрет на інтервалі U₂ –U₁, i =1,2,3,..., М -1.

При визначенні результуючої ФН необхідно абсциси точок перетину ФН нечітких підмножин ( наприклад, термів позитивни-1, негативний-2) з горизонтальними прямими. Найбільш просто це виконати для трикутних ФН.

Для ФН виду: = (1- u)^с, = u^с, u [0, 1]

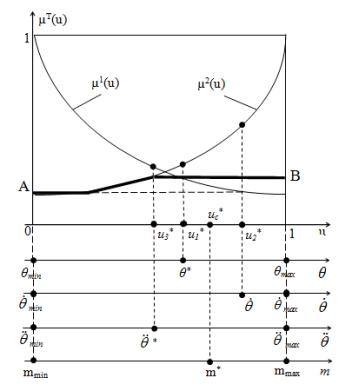
Рисунок 1 - Експоненціальні ФН на універсальній множині змінних з результуючою ФН (лінія АВ)

абсциси точок перетину визначаються як:

u^* = 1- і u^* = 1- . (3.40)

Для ФН дзвоноподібного виду:

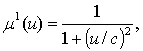
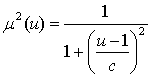, u [0, 1],

абсциси точок перетину визначаються як:

u^* = с 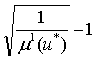і u^* = 1+ с 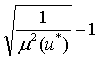. (8)

Для гаусових ФН виду (8) абсциси точок перетину визначаються як:

u^* = с і u^* = 1- с. (9)

Для експоненціальних ФН виду:

, , u [0, 1],

абсциси точок перетину визначаються як:

u^* = -ln і u^* = 1+ln. (10)

Остаточний вибір ФН для НР в САК можливий лише при оптимізації основних параметрів регулятора (діапазонів зміни ЛЗ, форми і параметрів ФН лінгвістичних величин).

При оптимізації параметрів цифрових регуляторів необхідно задавати критерій якості і функції впливу (керуючий і/або збурюючий вплив) на систему. Найбільш часто використовують один із квадратичних критеріїв якості, наприклад:

J = 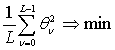, (11)

де помилка системи обчислюється з кроком моделювання h₀ , а число L визначає інтервал спостереження. Оптимальні параметри відповідають мінімальному значенню критерію якості, а мінімізація критерію якості автоматично приводить до оптимізації перехідних процесів в САК. Можна використовувати різні алгоритми умовної і безумовної оптимізації.

Розглянемо САК (рис.2) з цифровим НР і нестаціонарним ОК, «заморожена» ПФ якого визначається формулою: G(s) = =

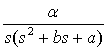
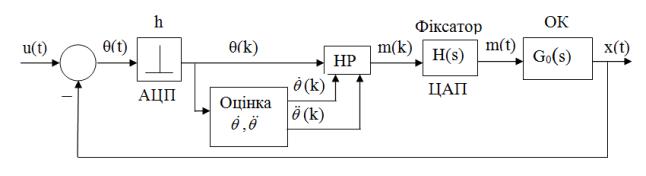
Рисунок 2 - Структурна схема САК з нечітким регулятором

Припустимо, що синтез НР виконаний при заданих законах зміни параметрів функції передачі ОК, вхідного впливу і трикутних ФН. При цьому вибрані без оптимізації (налаштування «вручну») діапазони зміни вхідних і вихідних параметрів НР (діапазони зміни змінних θ, , , m ) визначаються:

[θ_min , θ_max] = [-1,02; 1,02], [_{min , max}] = [-4; 4],

[_min , _max ] = [-24; 24] i [m_min , m_max] = [-1, 1].

Крок квантування в цифровому НР h = 0,01с, крок моделювання h₀ = 0,0005с. Квадратичний критерій якості має показник: J = 0,021.

Після оптимізації отримуємо наступні діапазони зміни вхідних і вихідних параметрів НР (діапазони зміни змінних θ, , , m ):

[θ_min , θ_max] = [-1,02; 1,02], [_{min , max}] = [-2,75; 2,75],

[_min , _max ] = [-16,52; 16,52] i [m_min , m_max] = [-1, 1].

Квадратичний критерій якості має показник: J = 0,0168.

Можна використати різні форми ФН (3)–(6) і, варіюючи одночасно коефіцієнтом с і діапазонами зміни вхідних і вихідних параметрів (діапазони зміни змінних θ, , , m), визначати мінімальне значення показника J.

Проведені розрахунки методом Хука-Дживса з використанням формул (3.39) – (3.44) дають наступні результати. Найбільше із мінімальних значеннь показника J одержується при використанні ФН, які визначаються за формулою (3.36), при наступних параметрах цифрового НР: с = 10^-4;

[θ_min , θ_max] = [-1,02; 1,02], [_{min , max}] = [-2,14; 2,14],

[_min , _max ] = [-22,23; 22,23] i [m_min , m_max] = [-1, 1].

Квадратичний критерій якості має показник: J = 0,0197.

Найменше із мінімальних значеннь показника J одержується при використанні експоненціальних ФН, які визначаються за формулою (7) і (8), при наступних параметрах цифрового НР: с =72,5;

[θ_min , θ_max] = [-1,02; 1,02], [_{min , max}] = [-3,75; 3,75],

[_min , _max ] = [-22,98; 22,98] i [m_min , m_max] = [-1, 1].

Квадратичний критерій якості має показник: J = 0,0136.

Таким чином, для розглянутої САК експоненціальні ФН є найкращими при вибраному критерію якості. З метою вибору оптимальних параметрів fuzzy-регуляторів із конкретних об’єктів керування слід проводити розрахунки із різних ФН і, використовуючи оптимізаційні програми, вибирати ФН, при яких обчислений показник якості J є мінімальним.

Висновок. За допомогою програм Opt_HD реалізовано алгоритм безумовної оптимізації методом Хука-Дживса параметрів fuzzy-регуляторів (діапазони зміни змінних , ) САК нестаціонарним ОК і продемонстровано результати дослідження точності відпрацювання САК із НР заданого закону зміни вхідного впливу. Оптимізація параметрів приводить до значного покращення якості СУ, яке характеризується величиною поточної помилки і чисельно визначається показником J.

1. Гостев В.И. Оптимизация параметров цифровых нечетких регуляторов / В.И.Гостев, И.П.Лесовой, А.Е.Чуприн // Радиоэлектроника Информатика Управление.- 2001.- С.148-151.

2. Архангельський В.І. Досвід розвитку і застосування систем функції-управління / В.І.Архангельський., І.Н.Богаенко та ін. // Автоматизація виробничих процесів. – 1997. - №2(5). – С.1-10.

3. Алиев Р.А. Неченткие модели управления динамическими системами / Р.А.Алиев, Э.Г.Захарова, С.В.Ульянов // Итоги науки и техники. Сер. Техническая кібернетика. – М.: ВИНИТИ АН СССР, 1990, т.29, С.127-201.