Россия, г. Нижний Новгород,
ТАЖИН
Юрий Александрович ©
независимый эксперт в области системно-финансового анализа,
экономических приложений Data Mining и Fuzzy-технологий
Использование методов исследования операций для
решения
типовых задач обоснования управленческих решений
(Часть 2)
В системном анализе одним из наиболее важных с практической точки зрения разделов моделирования является класс задач оптимального распределения ресурсов при линейных ограничениях. Так, в частности, задача построения межотраслевого баланса, которая впервые в мировой практике была поставлена в 1925 году талантливым русским математиком и выдающимся экономистом В.В. Леонтьевым /6, с.254-258/, основана именно на системе линейных уравнений-ограничений без выделения целевой функции.
В хозяйственной практике, например, в логистике запасов, а также транспортной логистике широко известна так называемая транспортная задача, позволяющая при соответствующих ресурсных ограничениях найти оптимальный по критерию минимальной стоимости план перевозок грузов. Транспортная задача является частным случаем общей задачи ЛП-N. Поэтому алгоритм её решения специфический – он более нагляден и прозрачен для ЛПР, нежели алгоритм симплекс-метода.
Рассмотрим следующую абстрактную модель, демонстрирующую применение симплекс-метода.
Найти оптимальный план х (х≥0) и оптимальное значение целевой функции f(x), используя процедуру симплекс-метода при заданной системе ресурсных ограничений.
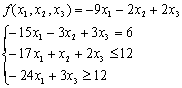
Содержательная интерпретация хозяйственной ситуации, моделируемой заданной целевой функцией и системой ресурсных ограничений может быть самой различной. Простейший пример из хозяйственной практики – построение оптимального плана продаж трёхпродуктового ассортимента «наиболее ходовых» товаров в малой торговой точке, позволяющего минимизировать издержки её владельца.
Решение этой задачи будет следующим.
Начальный этап. Для того, чтобы перейти к ограничениям-равенствам введём фиктивную переменную х4:
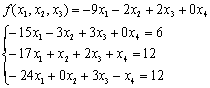
Далее, после того, как совершён формальный переход к ограничениям-равенствам, начинает «работу» собственно алгоритм симплекс-метода.
1 шаг симплекс-метода:
|
№ стр. |
х1 |
х2 |
х3 |
х4 |
|
Комментарий при переходе к шагу 2 |
|
1 |
–15 |
–3 |
3 |
0 |
6 |
стр.1/3 |
|
2 |
–17 |
1 |
2 |
1 |
12 |
+стр.1× (–2/3) |
|
3 |
–24 |
0 |
3 |
–1 |
12 |
+стр.1× (–3/3) |
|
4 |
–9 |
–2 |
2 |
0 |
f |
+стр.1× (–2/3) |
Максимальный положительный элемент в функциональной строке (стр.4): 2.
Ключевой столбец помечен красным цветом.
min(6/3; 12/2; 12/3) = 6/3 = 2. Ключевая строка помечена красным цветом.
Ключевой элемент – на пересечении ключевых строки и столбца: 3 (выделен жирным курсивом).
2 шаг симплекс-метода:
|
№ стр. |
х1 |
х2 |
х3 |
х4 |
|
комментарий при переходе к шагу 3 |
|
1 |
–5 |
–1 |
1 |
0 |
2 |
|
|
2 |
–7 |
1 |
0 |
1 |
8 |
|
|
3 |
–9 |
3 |
0 |
–1 |
6 |
|
|
4 |
1 |
0 |
0 |
0 |
f |
|
Максимальный положительный элемент в функциональной строке (стр.4): 1.
Ключевой столбец помечен цветом.
Поскольку в ключевом столбце нет положительных элементов, то исходная задача не имеет решения.
Таким образом, мы получили следующий ответ: задача при заданной системе
ограничений не имеет конечного решения. Почему это произошло? Вспомним
решение аналогичной задачи с меньшей размерностью: ЛП-2. Там область
ограничений являлась конечным (в смысле измеримости)
множеством с замкнутой выпуклой границей. Здесь же, совершенно очевидно,
область ограничений получилась незамкнутой, т.е. бесконечной в смысле измеримости
– что-то вроде двугранного (или многогранного) угла в трёхмерном пространстве ![]() . Можно попытаться построить эту область с помощью методов
аналитической геометрии, изобразить её на плоскости в «квазипространственном»
варианте. Если вы неплохой художник-график, и к тому же знаете аналитическую
геометрию в рамках стандартного университетского курса.
. Можно попытаться построить эту область с помощью методов
аналитической геометрии, изобразить её на плоскости в «квазипространственном»
варианте. Если вы неплохой художник-график, и к тому же знаете аналитическую
геометрию в рамках стандартного университетского курса.
Но даже в этом случае, с законами начертательной геометрии вы всё равно не поспорите – пропорции вашего рисунка будут искажены проективным отображением. Однако и без этого должно быть интуитивно ясно – построенная вами граница является бесконечной. На этом моменте следует остановиться подробнее.
В практическом аспекте бесконечность области ограничений (незамкнутость её границы) означает, что исследователю, чтобы получить конечное решение в виде тройки фиксированных значений независимых переменных (х1, х2, х3) следует изменить какое-либо из ресурсных ограничений. Либо, если по экономическому смыслу задачи решение обязательно должно быть конечным, такой результат свидетельствует об ошибке в каком-то из ресурсных ограничений.
Как правило, изменение знака ресурсного ограничения-неравенства на противоположный снимает эту проблему. Ещё один из вариантов решения возникшего парадокса «бесконечной области ограничений» состоит во введении дополнительного (в некотором смысле, «потерянного» при начальной постановке задачи) ограничения-неравенства с противоположным знаком при правой части. Здесь следует подчеркнуть, что это равенство должно обязательно вытекать из экономического смысла поставленной задачи. Иначе решение будет бессодержательным: формально правильным, но не имеющим никакого практического смысла.
Вообще говоря, задача оптимизации вида ЛП-N, решаемая в общем случае с помощью алгоритма симплекс-метода полезна для построения и расчёта оптимального баланса ресурсов (трудовых, материальных, финансовых) в какой-либо хозяйственной системе при заданном критерии оптимизации и заданной системе ресурсных ограничений. При этом система ресурсных ограничений должна быть полной, т.е. обеспечивающей замкнутость (ограниченность) области определения целевых переменных. Это свойство системы ресурсных ограничений называется совместностью.
Рассмотренный выше пример позволяет сделать следующие выводы.
1) Следует внимательно анализировать систему ресурсных ограничений. Если в ней содержатся ошибки (неполнота, неверные знаки в неравенствах), это может привести к невозможности нахождения конечного решения. Система ограничений должна быть совместной по независимым переменным.
2) Целевая функция и ограничения должны быть обязательно линейными функциями относительно независимых переменных.
3) Коэффициенты линейных функций должны быть определёнными – фиксированными постоянными величинами.
Последний, на первый взгляд, тривиальный вывод позволяет понять важную особенность применимости моделей ЛП-N и алгоритма симплекс-метода. Он адекватно описывает только те хозяйственные проблемы, которые допускают чёткую структуризацию и полную определённость.
На практике это (полная определённость) случается не так часто, но в ряде практически важных случаев изменчивость указанных коэффициентов за рассматриваемый исследователем временной промежуток пренебрежимо мала, и поэтому неопределённостью можно пренебречь.
Достаточно частой, однако, бывает противоположная ситуация – неопределённость исхода хозяйственной ситуации очень высока. В этом случае для системного моделирования и проведения расчётов обычно используется математический аппарат теории матричных игр, к рассмотрению которого мы переходим далее.
Отметим, что согласно /3, с.294/ под неопределённостью следует понимать отсутствие, неполноту, недостаточность информации об объекте, процессе или явлении или неуверенность исследователя в достоверности имеющейся у него информации.
Итак, пусть заданы три прямоугольных игровых («платёжных») матрицы, описывающие модель каждой конкретной ситуации выбора в условиях максимальной («полной») неопределённости.
1) 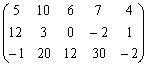
2) 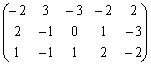
3) 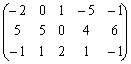
Требуется решить таким образом абстрактно сформулированные задачи выбора оптимального решения в условиях полной неопределённости по типу матричных игр /5, с.178-190/.
Согласно алгоритму решения матричных игр /3, с.297-303; с.306-324/:
1) Для заданной платёжной матрицы находим верхнюю и нижнюю цену игры:
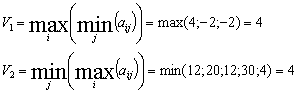
Получили, что V1 = V2 = V = 4, т.е. игра имеет седловую точку, которая и будет её решением:
S* = (i,j,V) = (1,4,4).
2) Для заданной платёжной матрицы находим верхнюю и нижнюю цену игры:
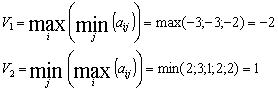
Получили, что V1 ≠ V2, т.е. игра не имеет седловой точки, решение ищем в смешанных стратегиях.
Уменьшаем размерность исходной платёжной матрицы за счёт исключения доминирующих строк/столбцов:
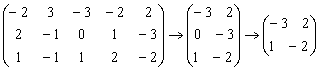
Из последней матрицы находим вероятности стратегий и цену игры:
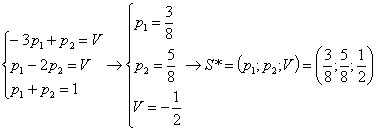
3) Для заданной платёжной матрицы находим верхнюю и нижнюю цену игры:
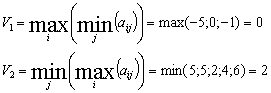
Получили, что V1 ≠ V2, т.е. игра не имеет седловой точки, решение ищем в смешанных стратегиях.
Уменьшаем размерность исходной платёжной матрицы за счёт исключения доминирующих строк/столбцов:
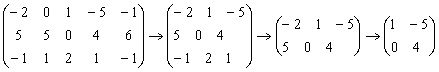
Из последней матрицы находим вероятности стратегий и цену игры:
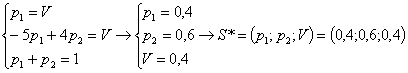
Ответы: 1) S* = (1,4,4). 2) ![]() 3)
3) ![]() .
.
В первом случае наша модель описывает нахождение компромиссной стратегии двух игроков с противоположными интересами («непримиримых» конкурентов). Седловая точка определяет значения номеров оптимальных стратегий для первого (i) и второго игрока (j), максимальный выигрыш первого и минимальный проигрыш второго игрока (V – в некоторых условных единицах).
Во втором и третьем случаях модель описывает нахождение компромиссной
стратегии двух игроков (конкурентов), которые договорились о разделе сфер своего
рыночного влияния. В этих случаях найденное компромиссное решение определяет их
возможные удельные веса влияния на рынок (логические вероятности реализации
смешанных стратегий – ![]() ) и величину выигрыша/проигрыша первого/второго игроков (V) соответственно.
) и величину выигрыша/проигрыша первого/второго игроков (V) соответственно.
Следует в заключение сказать, что в настоящее время развитие теории игр вышло далеко за пределы рассмотренных нами простейших случаев (парных игр) с нулевой суммой. Объём статьи не позволяет обстоятельно рассмотреть все указанные аспекты практических приложений. Некоторые интересные и полезные системные модели рассмотрены, например, в /1/, /4/, /7/, /8/, /9/. Данные монографии по нашему мнению, вполне можно рекомендовать как практические пособия для оценки и исследования широкого спектра предпринимательских рисков.
Кроме того, в настоящее время существуют и другие методы моделирования хозяйственных ситуаций/систем, обладающие, с одной стороны – несравненно более мощным по своим аналитическим и прогнозным возможностям математическим аппаратом, а с другой – позволяющие избавиться от серьёзной практической проблемы обоснования субъективно устанавливаемых параметров /10/. Достаточно подробный анализ возможностей этих методов дан, в частности, в монографии /2, с.22-42/.
Библиография
1. Анфилатов В.С. и др. Системный анализ в управлении. – М.: Финансы и статистика, 2009. – 368 с. ISBN 978-5-02435-3.
2. Бочарников В.П. Fuzzy-технология: математические основы. Практика моделирования в экономике. – СПб: Наука, 2001. – 328 с. ISBN 966-521-082-3.
3. Бережная Е.В., Бережной В.И. Математические методы моделирования экономических систем. – М.: Финансы и статистика, 2002. – 368 с. ISBN 5-279-02291-8.
4. Воробьёв С.Н., Балдин К.В. Управление рисками в предпринимательстве. – М.: ИТК «Дашков и К0», 2006. – 772 с. ISBN 5-94798-553-0.
5. Конюховский П.В. Математические методы исследования операций. – СПб.: Питер, 2001. – 192 с. ISBN 5-318-00027-4.
6. Леонтьев В. Баланс народного хозяйства. // Плановое хозяйство (Издание Госплана СССР, декабрь 1925 года). №12, 1925. – с.254-258.
7. Рыхтикова Н.А. Анализ и управление рисками организации, М.: Форум, 2009. – 240 с. ISBN 978-5-91134-195-4.
8. Шапкин А.С. Экономические и финансовые риски. Оценка, управление, портфель инвестиций. – М.: ИТК «Дашков и К0», 2006. – 544 с. ISBN 5-94798-696-5.
9. Шоломицкий А.Г. Теория риска. Выбор при неопределённости и моделирование риска. – М.: ИД ГУ ВШЭ, 2005. – 400 с. ISBN 5-7598-0280-1.
10. Alexey Nedosekin.
Fuzzy financial management. Russia,
Moscow, AFA Library, 2003. – 184 с. Источник:
www.sedok.narod.ru .