Экономические
науки / 8.Математические
методы в экономике
Семененко О.Г.
Переяслав-Хм. ДПУ імені Г. Сковороди, Україна
МОДЕЛЬ СИНТЕЗУ ЛАНЦЮГІВ
ПОСТАЧАННЯ МОЛОКА ТА МОЛОЧНОЇ ПРОДУКЦІЇ
Основною стратегією управління в ланцюгах
постачання молока та молокопродукції стає
організація оптимального управління потоком товарів та сутніми потоками
в каналах розподілу, що мінімізує сукупні витрати та збільшує рентабельність
діяльності кожної ланки ланцюга і збільшує цінність готового продукту та рівень
задоволення потреб кінцевого споживача.
До таких витрат можна віднести: витрати
транспортування; витрати зберігання товару; витрати на закупівлю та просування;
витрати на створення логістичної системи управління,витрати на інтеграційні
процеси товарного ринку.
В види моделей що можуть застосовуватися при
оптимізації управління товаропотоком
поділяються в залежно від місця розподілу, комплексів параметрів та
характеристик процесу на: моделі проектування та організації;- моделі логістичного
контролінгу; моделі логістичного аудиту; моделі логістичного консалтингу.
В загальному вигляді моделі, що використовують при
аналізі та синтезі ланцюгів постачання поділяються на наступні: вибір оптимального числа і розміщення
підприємств ланцюга (в тому числі і складів); створення оптимальних пропорцій між виробництвом, складуванням,
перевезенням та продажем молоко продукції; оптимізація (мінімізація) логістичних витрат ланцюга постачання; встановлення оптимального рівня інтеграції
(кооперації) в системі поставок, що враховує цілі та задачі кожної
організаційної структури; оптимізація
проходження інформаційного потоку через ланцюг, тощо.
Прикладом моделі, що може використовуватися для
синтезу логістичних ланцюгів постачання є модель
комерційцно-виробничо-транспортної багато продуктової задачі на мінімум витрат,
яка дозволяє визначити склад підприємств логістичного ланцюга, оптимальні
перевезення та розподіл молоко продукції, якщо відмий попит. Дана модель
розроблена на основі моделей оптимального планування та кооперації галузевого
виробництва.
Для опису моделі
системи товаропостачання молока та молокопродукції необхідно ввести додаткові
умови, припущення: поставка товарів в
торгівельну мережу та сировини на переробні заводи проходить миттєво, тобто
спостерігається відсутність запасів, та витрат на їх збереження; кластер
найвигідніших постачальників, виробників та посередників вже визначений;
обраховані планові показники по поставках в торгівельну мережу, потужності
переробних підприємств, прогнозні показники попиту на продукцію кожного виду по
кожному магазину від кожного постачальника.
Для такої моделі
доречно розглядати різні групи постачальників, згрупованих наприклад за
однаковим асортиментом.
Основна мета
оптимізації – полягає у визначенні
оптимальних структурних пропорцій поставок між виробниками молокопродукції,
переробними підприємствами та торгівельною мережею, що мінімізують транспортні
витрати та собівартість.
Нехай маємо: мережу з К-магазинів
оптово-роздрібної торгівлі, що займається разом збутом молока та молоко продукції та мають логістичний центр
розподілу. Кількість асортименту цих товарів (або їх замінників) – M; кількість
постачальників-заводів – N; L - кількість посередницьких та оптових структур, що
займаються збутом та перевезенням молока та молокопродукції від заводів
виробників до торгівельних підприємств; кількість підприємств, що займаються
виробництвом і постачанням молока-сировини (без господарств населення) – J; господарства населення,
що займаються виробництвом молока для переробних заводів здають продукцію на
приймальні пункти в загальній кількості – Н; І – кількість посередницьких
структур, що займаються постачанням молока сировини до переробних заводів.
Введемо позначення:
![]() - обсяг поставок
продукції виду
- обсяг поставок
продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину,
за w каналом розподілу без посередників;
-ого магазину,
за w каналом розподілу без посередників;
![]() - попит на
продукції виду
- попит на
продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину,
за w каналом розподілу без посередників;
-ого магазину,
за w каналом розподілу без посередників;
![]() собівартість одиниці
продукції виду
собівартість одиниці
продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину,
за w каналом розподілу без посередників;
-ого магазину,
за w каналом розподілу без посередників;
![]() транспортні
витрати на перевезення одиниці продукції виду
транспортні
витрати на перевезення одиниці продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину,
за w каналом розподілу без посередників;
-ого магазину,
за w каналом розподілу без посередників;
![]() обсяг поставок
продукції виду
обсяг поставок
продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину,
за w каналом розподілу через посередників;
-ого магазину,
за w каналом розподілу через посередників;
![]() попит на
продукції виду
попит на
продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину,
за w каналом розподілу через посередників;
-ого магазину,
за w каналом розподілу через посередників;
![]() собівартість
одиниці на продукції виду
собівартість
одиниці на продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину,
за w каналом розподілу через посередників;
-ого магазину,
за w каналом розподілу через посередників;
![]() транспортні
витрати на перевезення одиниці продукції виду
транспортні
витрати на перевезення одиниці продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину,
за w каналом розподілу через посередників;
-ого магазину,
за w каналом розподілу через посередників;
![]() - обсяг поставок
сировини від
- обсяг поставок
сировини від ![]() -ого виробника ((h) – приймального пункту) до
-ого виробника ((h) – приймального пункту) до ![]() заводу за w каналом розподілу без посередників;
заводу за w каналом розподілу без посередників;
![]() - план поставок
сировини від
- план поставок
сировини від ![]() -ого виробника ((h) – приймального пункту) до
-ого виробника ((h) – приймального пункту) до ![]() заводу за w каналом розподілу без посередників;
заводу за w каналом розподілу без посередників;
![]() - собівартість
одиниці сировини від
- собівартість
одиниці сировини від ![]() -ого виробника ((h) – приймального пункту) до
-ого виробника ((h) – приймального пункту) до ![]() заводу за w каналом розподілу без посередників;
заводу за w каналом розподілу без посередників;
![]() - транспортні
витрати на перевезення одиниці сировини від
- транспортні
витрати на перевезення одиниці сировини від ![]() -ого виробника ((h) – приймального пункту) до
-ого виробника ((h) – приймального пункту) до ![]() заводу за w каналом розподілу без посередників;
заводу за w каналом розподілу без посередників;
![]() - обсяг поставок сировини від
- обсяг поставок сировини від ![]() -ого виробника ((h) – приймального пункту) до
-ого виробника ((h) – приймального пункту) до ![]() заводу за w каналом розподілу через посередників;
заводу за w каналом розподілу через посередників;
![]() - план поставок
сировини від
- план поставок
сировини від ![]() -ого виробника ((h) – приймального пункту) до
-ого виробника ((h) – приймального пункту) до ![]() заводу за w каналом розподілу через посередників
заводу за w каналом розподілу через посередників
![]() - собівартість одиниці сировини від
- собівартість одиниці сировини від ![]() -ого виробника ((h) – приймального пункту) до
-ого виробника ((h) – приймального пункту) до ![]() заводу за w каналом розподілу через посередників;
заводу за w каналом розподілу через посередників;
![]() - транспортні витрати на перевезення одиниці сировини від
- транспортні витрати на перевезення одиниці сировини від
![]() -ого виробника ((h) – приймального пункту) до
-ого виробника ((h) – приймального пункту) до ![]() заводу за w каналом розподілу через посередників;
заводу за w каналом розподілу через посередників;
![]() - загальний попит
в торгівельній мережі на продукцію m від r-ого виробника;
- загальний попит
в торгівельній мережі на продукцію m від r-ого виробника;
![]() - потужність r – ого переробного підприємства;
- потужність r – ого переробного підприємства;
![]() - план випуску
продукції виду m
від r – переробного підприємства;
- план випуску
продукції виду m
від r – переробного підприємства;
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Запишемо загальну модель задачі: Згідно умов можна
скласти обмеження оптимізаційної моделі :
1)
Обсяг поставок продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину з
через логістичний центр, не менше планової.
-ого магазину з
через логістичний центр, не менше планової.
![]() ,
, ![]() ,
, ![]() ,
, ![]() (1)
(1)
2) Обсяг поставок продукції виду ![]() від
від ![]() заводу
через
заводу
через ![]() -го ділера до
-го ділера до ![]() - ого магазину
з через логістичний центр, , не менше планової.
- ого магазину
з через логістичний центр, , не менше планової.
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
,![]() (2)
(2)
3)
Обсяг поставок продукції виду ![]() від
від ![]() заводу до
заводу до ![]() -ого магазину з
напряму, не менше планової.
-ого магазину з
напряму, не менше планової.
![]() ,
, ![]() ,
, ![]() ,
, ![]() (3)
(3)
4)
Обсяг поставок продукції виду ![]() від
від ![]() посередника до
посередника до ![]() -ого магазину з
напряму , не менше планової
-ого магазину з
напряму , не менше планової
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() (4)
(4)
5)
Умова зв’язності сума поставок будь-якої структури повинна дорівнювати
попиту на цю продукцію :
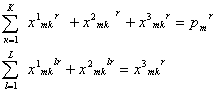
![]() ,
, ![]() ,
, ![]() ,
, ![]() (5)
(5)
6)
Умова завантаження потужностей переробних підприємств:
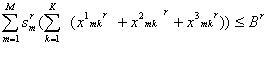
![]() ,
, ![]() ,
, ![]() (6)
(6)
7)
Умова виконання плану по кожному виду продукції для кожного заводу
![]()
![]() ,
, ![]() ,
, ![]() (7)
(7)
8) Обсяг поставок сировини від ![]() -ого виробника до
-ого виробника до ![]() заводу напряму
не менше планової:
заводу напряму
не менше планової:
![]()
![]() (8)
(8)
9) Обсяг поставок сировини від ![]() -ого виробника до
-ого виробника до ![]() заводу через
і-ого посередника не менше планової:
заводу через
і-ого посередника не менше планової:
![]()
![]() ,
, ![]() , (9)
, (9)
10) Обсяг поставок сировини від господарств
населення до ![]() заводу через
приймальні пункти:
заводу через
приймальні пункти:
![]() ,
, ![]() , (10)
, (10)
11) Обсяг поставок сировини від господарств
населення до ![]() заводу через
і-ого посередника не менше планової:
заводу через
і-ого посередника не менше планової:
![]()
![]() ,
, ![]() (11)
(11)
12)
Умова зв’язності сума поставок будь-якої структури повинна бути не більша
ніж потужність переробного підприємства:
![]()
![]()
![]() (12)
(12)
![]()
![]()
![]()
12) Умова невід’ємності змінних:
![]()
![]()
![]()
![]()
![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() (13)
(13)
13) Критері йоптмізації: ми
пропонуємо використовувати багатопараметричну оптимізацію, що
розглядає наступні функції цілі:
І.
мінімум
собівартості молоко продукції та сировини
ІІ.
мінімум транспортних витрат на перевезення сировини та готової продукції
ІІІ. Можливою
реалізацією багатопараметричної оптимізації є узагальнена цільова функція Foб, яка записується таким чином.
![]()
де Fk- к-ая цільова функція
Fkнopм - нормоване
значення к-ої цільової функції
s – кількість складених функцій
![]() - коефіцієнт ваги к-ої цільової функції.
- коефіцієнт ваги к-ої цільової функції.
При цьому перед складовими
цільової функції, які максимізуються, ставиться знак плюс, перед тими, що
мінімізуються - мінус. Для формування узагальненої цільової функції необхідно знати ![]() і Fkнopм Значення Fkнopм приймаються при максимізації к-ой
складової цільової функції: Fkнopм = Fkmax . При її мінімізації: Fkнopм = Fkmin .
і Fkнopм Значення Fkнopм приймаються при максимізації к-ой
складової цільової функції: Fkнopм = Fkmax . При її мінімізації: Fkнopм = Fkmin .
Тоді функції цілі нашої задачі
набувають вигляду:
1)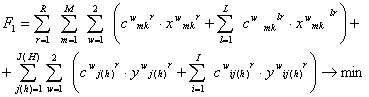 (14)
(14)
2)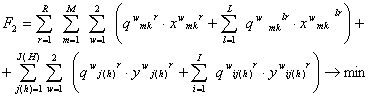 (15)
(15)
3)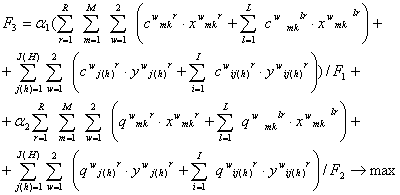 (16)
(16)
де ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,
, ![]()
Ця модель використовує дискретні
змінні (данні задачі беруться в кожний окремий період часу) і існують деякі
обмеження на застосування кінцевих (не наближених методів) розв’язку для цієї
задачі. Тому за наявності програмного
забезпечення для такої моделі більше підходять методи наближені, що зводься до
наступного: єдина задача розбивається на виробничу, комерційно-збутову та
відповідні транспортні частини. Знаходять оптимальні оцінки по кожному блоку.
Тоді рішення початкової задачі, що оптимізує пропорції постачання виконується
ітеративним шляхом, за допомогою коректирування всіх 4 планів.
Рішення розглянутої
оптимізаційної моделі не є остаточними планом постачання в логістичній системи
товаропросування. Вона одна з багатьох інших моделей (і не тільки
математичних), які застосовуються для створення оптимального управління в
ланцюгах постачання молока та молоко продукції.