к.т.н.
Турганбай К. Е., магистр Болаткызы М
Казахского
агротехнического университета имени С.Сейфуллина, Казахстан
ХАОС В ПРОСТЫХ МОДЕЛЯХ ДИНАМИЧЕСКИХ СИСТЕМ
О динамической системе [1] говорят в том случае, если можно
указать такой набор величин, называемых динамическими переменными и
характеризующих состояние системы, что их значения в любой последующий момент
времени получаются из исходного набора по определенному правилу. Это правило
задает оператор эволюции системы. Если состояние системы задается набором N
величин, то изменение состояния во времени, или динамику системы, можно
представить как движение точки по траектории в N-мерном фазовом пространстве,
которую называют фазовой траекторией.
Когда-то в понятие динамической
системы вкладывали чисто механическое содержание, имея в виду набор тел,
связанных силовыми взаимодействиями и подчиняющихся системе дифференциальных
уравнений, вытекающих из законов Ньютона. По мере развития науки понятие
динамической системы становилось шире, охватывая объекты разной природы.
Современное понятие динамической системы это результат длительной эволюции
научных представлений и синтеза достижений многих дисциплин. Оно подразумевает
возможность задания оператора эволюции любым способом, не обязательно
дифференциальным уравнением. В частности, в последнее время и в теоретических
исследованиях, и в работах прикладного характера очень часто рассматривают
системы с дискретным временем, которые описываются рекуррентными отображениями
[2]. В этом случае
под фазовой траекторией следует понимать некоторую дискретную
последовательность точек в фазовом пространстве.
Выделяют два класса
динамических систем — консервативные и диссипативные.
В физике свойство
консервативности понимается как сохранение энергии. В частности, механические
колебательные системы в отсутствие трения относятся к консервативным системам.
В присутствии трения механическая энергия не сохраняется, а постепенно
рассеивается (диссипирует) и переходит в тепло, т. е. в энергию
микроскопического движения молекул, составляющих систему и ее окружение.
Строго говоря, в этом случае временная эволюция должна определяться не только
состоянием самой системы, но и окружением. Все же и в этой ситуации описание в
рамках концепции динамических систем, заданных, например, дифференциальными
уравнениями, очень часто оказывается разумным и достаточно точным. Это будет
уже диссипативная динамическая система [3].
Пусть мы имеем некоторую
динамическую систему, т.е. задано фазовое пространство и указан оператор
эволюции. Вместо одной системы рассмотрим ансамбль, состоящий из большого количества
ее идентичных копий, причем все представители ансамбля могут отличаться друг
от друга только лишь начальными условиями. В фазовом пространстве ансамбль
представляется облаком изображающих точек. С течением времени каждая
изображающая точка перемещается в фазовом пространстве, как предписано динамическими
уравнениями системы, так что форма облака и его размеры будут меняться.
Может случиться, что
объем облака в процессе временной эволюции будет оставаться постоянным. Это
характерно для консервативных систем, к которым относятся, в частности,
рассматриваемые (Рис.1) в классической механике гамильтоновы системы.
Что касается
диссипативных систем, то для них характерно, что с течением времени облако
изображающих точек «съеживается» и концентрируется в итоге на одном или
нескольких аттракторах — подмножествах фазового пространства, обладающих
обычно нулевым фазовым объемом.
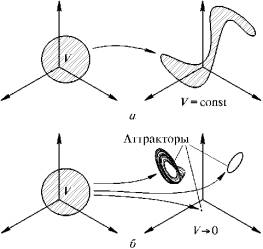
Рисунок 1. К определению
консервативных (а) и диссипативных (б) динамических систем
С
точки зрения динамики во времени, это означает, что режим, возникающий в
системе, предоставленной самой себе в течение длительного времени, становится
не зависящим от начального состояния (по крайней мере, при вариации начальных
условий в некоторых конечных пределах).[1]
Одним из важных понятий
теории динамических систем является понятие инвариантного множества. Множество
точек фазового пространства называют инвариантным в том случае, если фазовая
траектория, стартующая из любой его точки, целиком принадлежит этому
множеству. Любой аттрактор есть инвариантное множество, но не наоборот.
Неустойчивые неподвижные точки, неустойчивые замкнутые орбиты — это тоже
инвариантные множества. В отличие от аттракторов, которые имеют место только в
диссипативных системах, инвариантные множества встречаются и в диссипативных,
и в консервативных динамических системах [4].
Следует четко
осознавать, что понятие динамической системы есть теоретическая абстракция, так
же как многие другие привычные и полезные научные абстракции (материальная
точка, абсолютно твердое тело, несжимаемая жидкость, идеальный газ). Реальные
объекты могут рассматриваться как динамические системы только в определенном
приближении, в той мере, в какой при описании динамики можно игнорировать
тонкие детали внутренней структуры системы и ее взаимодействие с окружающим
миром.
Хаотические режимы
характеризуются нерегулярным, похожим на случайный процесс, изменением
динамических переменных во времени [1,4]. В диссипативных системах хаос ассоциируется с
наличием в фазовом пространстве странных аттракторов — сложно устроенных
фрактальных множеств, притягивающих к себе все траектории из некоторой
прилегающей области.
Список использованной литературы
1.
С.П.Кузнецов.
Динамический хаос- М.: Физматлит, 2001.-296с.
2.
Ашимов
А.А., Сакабеков А.С., Боровский Ю.В., Волобуева О.П., Об алгоритмах
исследования аттракторов динамических систем. Вестник МОиН РК, НАН РК, №3,
2002. - 4-10 стр.
3.
Каток
А.Б., Хасселблат Б. Введение в современную теорию динамических систем. –М.:
Факториал, 1999.-798 с.
4.
Гукенхеймер
Дж., Холмс Д. Нелинейные колебания, динамические системы и бифуркации векторных
полей.-М.: Наука, 2002.-560 с.