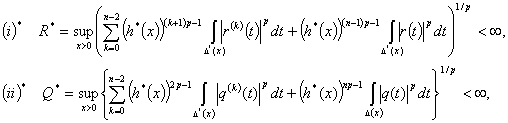Математика/1.
Дифференциальные и интегральные уравнения
Карсыбаева З.С., Мырзагалиева А.Х.
Евразийский национальный
университет, г. Астана, Казахстан
Об ограниченности одного
дифференциального оператора
в пространствах Соболева
Пусть 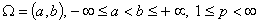 . Через
. Через  обозначим
пространство Лебега функций
обозначим
пространство Лебега функций  с нормой
с нормой
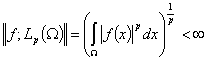 ,
,
соответственно
пространство Соболева 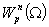 с конечной нормой
с конечной нормой
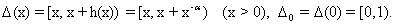
Определение
1. Будем говорить, что v(t) удовлетворяет условию медленного колебания относительно
h(x), если существуют постоянные 0<b1<b2
такие, что
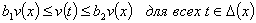 . (2)
. (2)
Положим
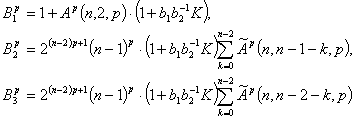 (3)
(3)
Здесь 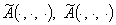 наилучшие постоянные в неравенствах Соболева (см. ниже оценки (6)
и (7)),
наилучшие постоянные в неравенствах Соболева (см. ниже оценки (6)
и (7)), 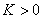 некоторая постоянная.
некоторая постоянная.
Теорема
1. Пусть
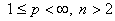 , функция
, функция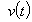 удовлетворяет условию медленного колебания (2) и существует
такая постоянная K>0, что
удовлетворяет условию медленного колебания (2) и существует
такая постоянная K>0, что
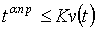 , для любого t∊∆(x). (4)
, для любого t∊∆(x). (4)
Если 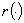 и
и 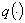 подчиняются условиям
подчиняются условиям
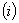
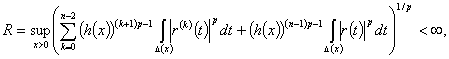
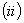
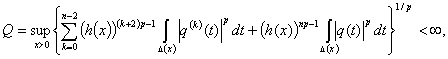
относительно 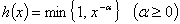 , то дифференциальный оператор L
есть ограниченный оператор, действующий из
, то дифференциальный оператор L
есть ограниченный оператор, действующий из 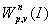 в
в 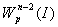 , при этом норма
, при этом норма
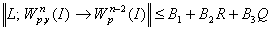 . (5)
. (5)
Доказательство теоремы 1 будет опираться на следующие
утверждения:
Утверждение
1.
Для функции 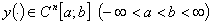 справедлива оценка
справедлива оценка
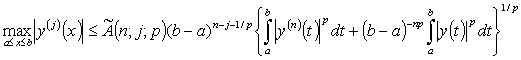 (6)
(6)
Утверждение
2. Пусть 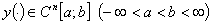 . Тогда для любого
. Тогда для любого 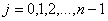 имеет место неравенство
имеет место неравенство
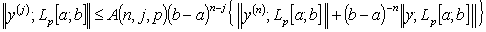 , (7)
, (7)
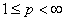 .
.
Оценки (6)
и (7) следуют из известных неравенств Соболева [1]:
Существует
постоянная 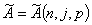 такая, что для любой
функции
такая, что для любой
функции 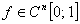 справедлива оценка
справедлива оценка
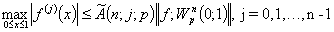 . (8)
. (8)
Существует
постоянная 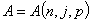 такая, что для любой
функции
такая, что для любой
функции 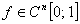 справедлива оценка
справедлива оценка
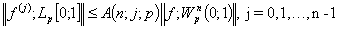 .
(9)
.
(9)
Здесь 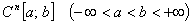 - класс всех
- класс всех 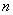 -раз непрерывно дифференцируемых функций на
-раз непрерывно дифференцируемых функций на 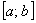 .
.
Доказательство
теоремы 1.
Имеем
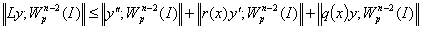 . (10)
. (10)
Представим 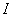 как дизъюнктивное
объединение
как дизъюнктивное
объединение 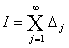 , где
, где 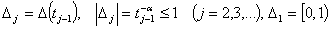 .
.
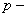 ая степень первого слагаемого в (10)
ая степень первого слагаемого в (10)
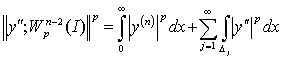 .
(11)
.
(11)
В силу
утверждения 2 (неравенство (7)) имеем
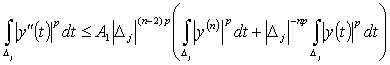 , (12)
, (12)
где 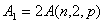 .
.
В неравенстве (12) ко второму слагаемому
в правой части применим условие (2). Тогда
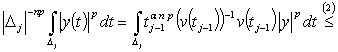
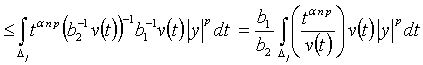 . (13)
. (13)
Теперь из
условия (4) теоремы 1 получим
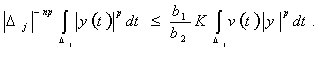 (14)
(14)
В
силу неравенств (12) и (14) имеем
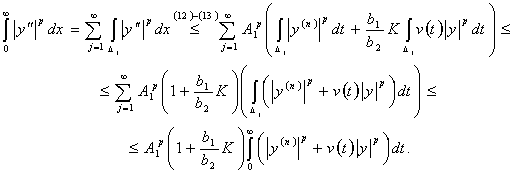 (15)
(15)
Итак,
получили, что
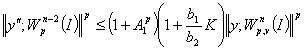 . (16)
. (16)
Рассмотрим второе слагаемое в (10)
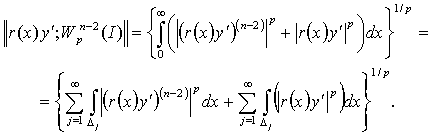 (17)
(17)
В (17) будем отдельно оценивать
каждое слагаемое:
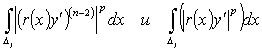 .
.
Имеем
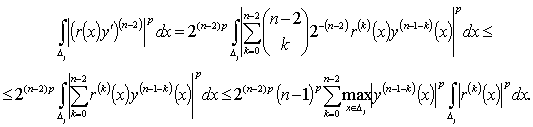 (18)
(18)
Применим к выражению 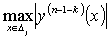 в (18) оценку (6)
в (18) оценку (6)
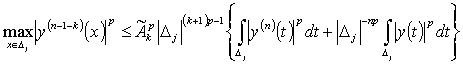 , (19)
, (19)
где 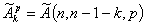 .
.
С учетом неравенства (19) перепишем
оценку (18)
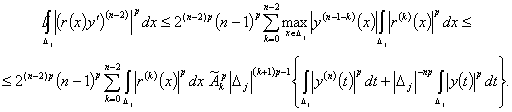 (20)
(20)
К выражению в фигурной скобке
применим неравенство (14). Получим
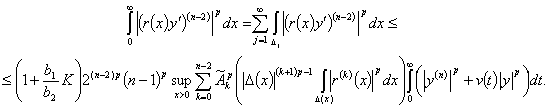 (21)
(21)
Вспомним,
что в основном неравенстве (10) идет оценка второго слагаемого, которое имеет
вид:
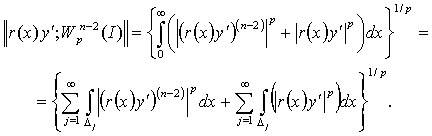
В этом выражении оценка первой
суммы сделана в (21), перейдем к оценке второй суммы
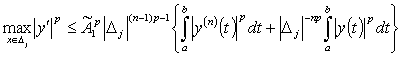 ,
,
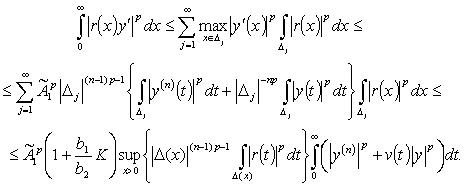
 (22)
(22)
Из (21) и (22) следует
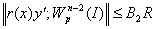 . (23)
. (23)
Выпишем третье слагаемое
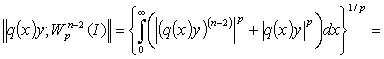
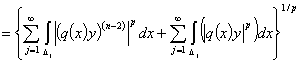 . (24)
. (24)
Для суммы в правой части (24) с
помощью аналогичных (17)-(22) выкладок получаем оценку
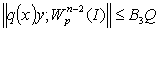 (25)
(25)
Из (16), (23) и (25) следует (5).
Теорема доказана.
Определение
2. Всякую положительную непрерывную
на 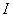 функцию h*(˖)
будем называть функцией длины (на
функцию h*(˖)
будем называть функцией длины (на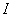 ).
).
Примеры функций длины:
1. 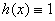
2. 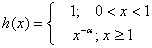 ,
,
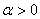 .
.
3. 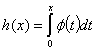 , где
, где 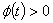 при
при 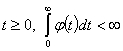 .
.
Теорема
2. Пусть 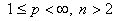 , функция
, функция 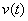 удовлетворяет условию
медленного колебания (2) относительно функции длины
удовлетворяет условию
медленного колебания (2) относительно функции длины 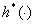 и существует такая
постоянная
и существует такая
постоянная 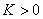 , что
, что
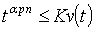 для любого
для любого 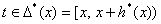 .
.
Если 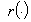 и
и 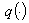 подчиняются условиям:
подчиняются условиям:
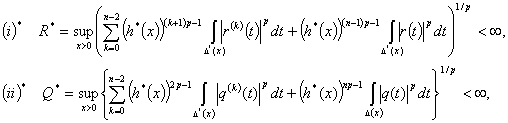

то дифференциальный оператор 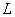 есть ограниченный оператор, действующий из
есть ограниченный оператор, действующий из 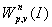 в
в 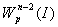 , при этом норма
, при этом норма
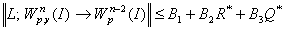 .
.
Замечание. Оценки норм для дифференциальных операторов в невесовых
пространствах Соболева ранее рассматривались в работе [2].
Литература:
1. Никольский С.М. Приближение функций многих переменных
и теоремы вложения. М.: Наука, 1977, 456 стр.
2. Мазья В.Г., Шапошникова Т.О. Мультипликаторы в
пространствах дифференцируемых функций. Л.: Изд-во Ленинградского университета,
1986, 404 стр.
![]() . Через
. Через ![]() обозначим
пространство Лебега функций
обозначим
пространство Лебега функций ![]() с нормой
с нормой 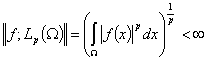 ,
,![]() с конечной нормой
с конечной нормой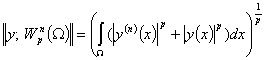 .
.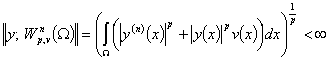 .
.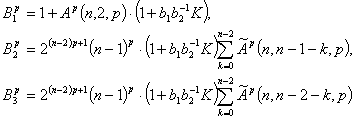
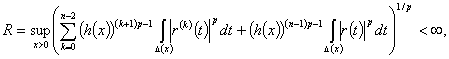
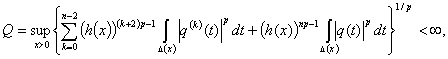
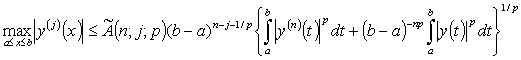
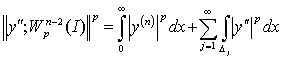 .
.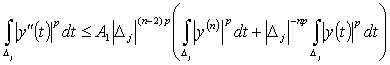 ,
,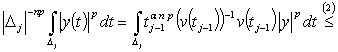
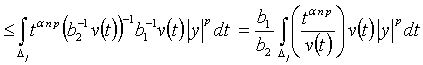 .
.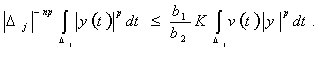
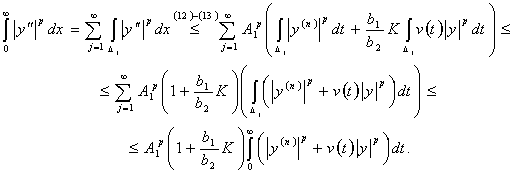
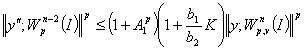 .
.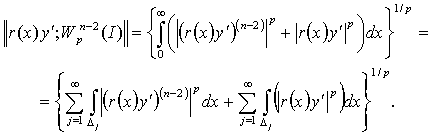
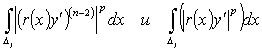 .
.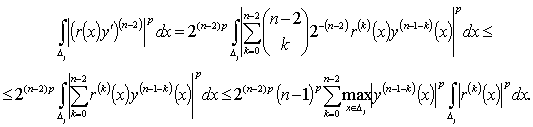
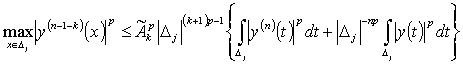 ,
,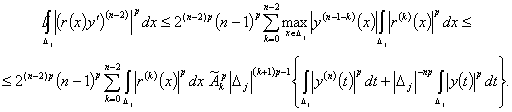
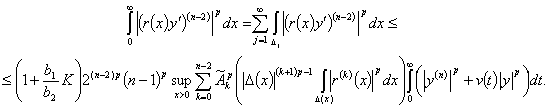 (21)
(21)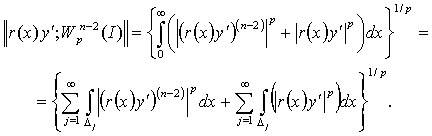
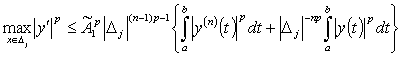
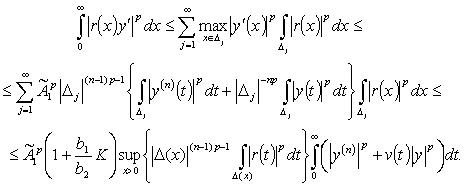
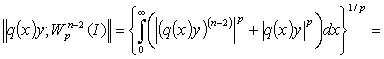
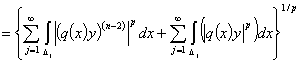 .
.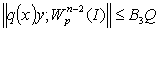
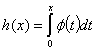 , где
, где 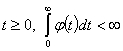 .
.