Математика/5. Математическое моделирование

Канд. техн. наук Пономарев Д.Ю.

Сибирский государственный аэрокосмический университет им. акад. М.Ф. Решетнева, Россия

Контурная тензорная модель инфокоммуникационной сети

Современные инфокоммуникационные сети обеспечивают передачу и обработку множества информационных потоков, используя большое количество устройств: коммутаторов, маршрутизаторов, серверов и т.д. Таким образом, структура связей между обслуживающими системами вступает во взаимодействие с процессами поступления информации и распределения трафика. Учет процессно-структурного взаимодействия классическими методами исследования обычно не производится [1]. Теория графов позволяет исследовать структуру сети без учета влияния процесса поступления информации, а теория массового обслуживания обеспечивает получение вероятностно-временных характеристик систем с неформализованным учетом влияния структуры.

Рассматриваемый в данной работе метод моделирования инфокоммуникационных сетей позволяет решить задачу учета процессно-структурного взаимодействия с использованием тензорного подхода. При этом обеспечивается хорошая формализация предлагаемого метода для программной реализации.

В соответствии с [2,3], учет процесса поступления информации для контурной тензорной модели производится через соотношение: , где – загрузка системы (ковариантная компонента), – интенсивность информационного потока (контравариантная компонента), – средняя длительность обслуживания, а учет структуры производится путем введения контурных интенсивностей. Множество контурных интенсивностей представляет собой множество путей передачи информации и определяет новое геометрическое пространство. Определяя взаимосвязь контурных интенсивностей и интенсивностей отдельных систем, можно учесть влияние структуры сети на распределение трафика. Таким образом, для получения распределения трафика в сети, необходимо составить матричное уравнение [2,3]: где – матрица перехода размерностью ( – число систем в сети; – количество контурных интенсивностей, равно числу возможных путей по сети), связывающая контурные интенсивности поступления и интенсивности поступления в отдельные системы; – матрица длительностей обслуживания в отдельных системах; – вектор контурных интенсивностей поступления; – вектор начальных значений загрузки.

Для построения модели инфокоммуникационной сети необходимо выделить пространство путей передачи информации и пространство систем распределения информации, определяющих состав сети.

Любой узел обработки информации можно представить в виде набора систем распределения информации (рис. 1).

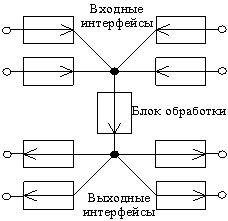
Рис. 1. Структура модели узла обработки информации

Первая группа систем это системы, обеспечивающие прием и предварительную обработку поступающей информации. Например, в компьютерной сети это прием битовой информации и формирование очереди из пакетов для дальнейшей обработки. Вторая группа, которая может состоять из одной системы, моделирует процесс обработки адресной и служебной информации в узле, необходимый для передачи пакетов по заданному маршруту с заданным качеством обслуживания. Для коммутаторов компьютерной сети, моделируемой системой является коммутационная матрица. Третья группа систем моделирует процесс отправки исходящей информации, т.е. связана с процессами формирования выходных очередей и отправкой пакетов.

Построение контурной тензорной модели рассмотрим на примере инфокоммуникационной сети, состоящей из трех узлов (рис.2).

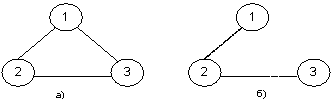
Рис. 2. Физическая (а) и логическая (б) топологии исследуемой сети

Рассмотрим случай, когда наложенная сеть для передачи информации имеет топологию дерево. В соответствии с представлением каждого узла, так как это описано выше (рис. 1), модель сети, состоящая из систем определяемых физической и логической топологиями, будет иметь следующий вид (рис. 3).

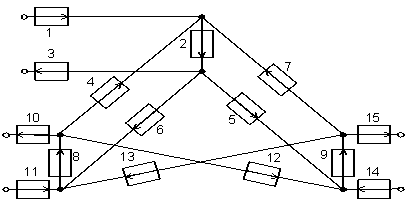
Рис. 3. Структура модели инфокоммуникационной сети

Системы 2, 8 и 9 являются системами обработки для узлов 1, 2 и 3 соответственно. Системы 1 и 3 моделируют обработку, соответственно, исходящих и входящих информационных потоков в узле 1. Аналогично для второго и третьего узлов. Для моделирования передачи информации от первого узла ко второму используется система 6, в обратную сторону система 4. Аналогично, для пары первый-третий узел: системы 5 и 7, для второго и третьего узлов: системы 12 и 13.

Для организации маршрутов передачи информации в данной сети необходимо проложить пути прохождения информационных потоков, используя рассмотренные системы. Например, для передачи информации из первого узла в третий, в соответствии с заданной структурой наложенной сети, путь передачи из первого узла в третий будет сформирован следующими системами: 1-2-6-8-12-9-15. Для получения замкнутых контуров рассматриваемых путей, введем мнимые системы (с 16 по 24), определяемые маршрутами прохождения информации (рис.4).

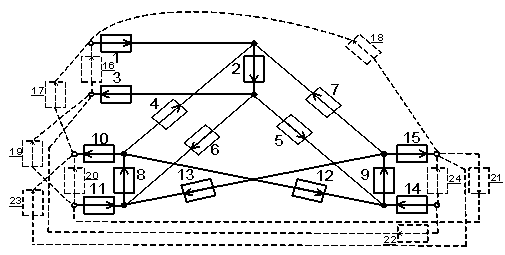
Рис.4 Добавление мнимых систем

Определив все маршруты передачи информации в исследуемой сети, включая обратные, составляем матрицу перехода [2,3] (приведена не полностью в связи с большой размерностью), элементы которой показывают участие систем в формировании пути:

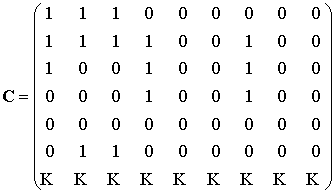
Первые три столбца данной матрицы определяются путями от абонентов первого узла: к абонентам первого, второго и третьего узлов, соответственно. Вторые три столбца устанавливаются путями от второго узла, аналогично: к первому, второму и третьему узлам. Третьи три столбца матрицы определяются аналогично. При этом в соответствии с древовидной структурой сети, пятая и седьмая строки представлены нулями, так как прямая связь между первым и третьим узлом в данной структуре не используется (рис.2б). Нижняя часть матрицы связана с мнимыми системами, участие которых в топологии определяется путями передачи информации.

Результатом решения матричного уравнения является вектор контурных интенсивностей при заданных начальных значениях загрузки

Полученные значения показывают распределение трафика по путям передачи информации. Распределение трафика по системам определяется, как: [2-3]. Для заданных начальных значений загрузки, распределение трафика по системам выглядит, как:

Дальнейшая задача заключается в определении вектора начальных загрузок, которые обеспечат задание требуемых интенсивностей потоков, создаваемых пользователями.

Таким образом, можно сделать вывод о возможности применения контурных тензорных моделей для распределения трафика в инфокоммуникационных сетях. Основными достоинствами такой модели являются: инвариантность моделей, хорошая формализуемость и простота программной реализации.

Литература:

1. Петров А.Е. Тензорная методология в теории систем. – М.: Радио и связь, 1985.

2. Пономарев Д.Ю. Тензорная методология в телекоммуникациях // Системы управления и информационные технологии. – 2006. – 1.1(23). – С. 161-165.

3. Пономарев Д.Ю. Контурный метод тензорного анализа инфокоммуникационных сетей // Materiály X mezinárodní vědecko - praktická konference «Efektivní nástroje moderních věd – 2014». Matematika. – Praha: Publishing House «Education and Science» s.r.o. – 2014. – S. 68-73.