К.ф.-м.н.
Яковлева Е.Н., Грудинина С.А.
Лесосибирский
педагогический институт – филиал
Сибирского
федерального университета, Россия
СВОЙСТВА ПОСЛЕДОВАТЕЛЬНОСТИ ФИБОНАЧЧИ.
Один из
известных историков математики Морис Кантор назвал Фибоначчи “блестящим
метеором, промелькнувшим на темном фоне западно-европейского средневековья”.
Наиболее
известной из сформулированных Фибоначчи задач является “задача о размножении
кроликов”, которая привела к открытию числовой последовательности 1, 1, 2, 3,
5, 8, 13,…, названной впоследствии “рядом Фибоначчи”.
Числа Фибоначчи или Ряд Фибоначчи - числовая последовательность,
обладающая рядом свойств. Например, сумма двух соседних чисел последовательности
дает значение следующего за ними (например, 1+1=2; 2+3=5 и т.д.), подтверждает
существование так называемых коэффициентов Фибоначчи, т.е. постоянных
соотношений.
Задача о кроликах.
Пусть
имеется пара кроликов. Известно, что от каждой пары кроликов каждый месяц
рождается новая пара кроликов, которая в свою очередь становится способной
производить потомство в возрасте одного месяца. Требуется определить, сколько
пар кроликов будет через n месяцев.
Решение
задачи.
Пусть fn число пар кроликов
после n месяцев. Число пар
кроликов после n+1 месяцев fn+1, будет равно числу пар
на n-ом месяце т.е. fn, плюс число пар
новорожденных кроликов. Поскольку кролики рождаются от пары кроликов возраста
больше одного месяца, новорожденных кроликов будет fn-1 пар. Следовательно,
справедливо отношение:
fn+1=fn + fn-1, (1)
причем f0=0, f1=1. (2)
Таким образом, получим
рекуррентную числовую последовательность
0,
1, 1, 2, 3, 5, 8,… (3)
Каждый член этой
последовательности, начиная с третьего, равен сумме двух предыдущих. Первые два
члена считаются заданными f0=0, f1=1.
Таким образом, “задача о
кроликах” свелась к решению фундаментального уравнения (1), т.е. к нахождению
общего члена последовательности fn
удовлетворяющего соотношению (1) при условиях (2).
Предположим,
что последовательность fn
имеет вид fn=λn, (4)
где λ –
вещественный параметр. Подставив fn
в (1) получим: λn+1= λn+λn-1, или,
эквивалентно, λn-1(λ2-λ-1)=0.
Так как fn ≠ 0 (n ϵ
N), последнее равенство
принимает вид:
λ2-λ-1=0,
(5)
которое представляет
собой квадратное уравнение по отношению к действительному параметру λ. Из (5) получим:
λ1=
, λ2= 
.
Таким
образом, последовательности: fn=
, fn= 
удовлетворяют равенству
(1). Отсюда заключаем, что уравнение (1) имеет много решений. В общем,
существует бесконечное число последовательностей, удовлетворяющих (1).
Например, последовательность вида: fn=c1+ c2
, (6)
где с1,с2
- фиксированные действительные константы, также удовлетворяет (1). Более того,
можно показать, что любая последовательность, удовлетворяющая равенству (1)
имеет вид (6).
Эта
последовательность однозначно определена, и однозначность обеспечивается
первыми двумя членами, т.е. начальными условиями (2). Подставляя n=0 и n=1 в (6), получим
линейную систему:
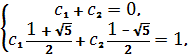с решением с1= 
, с2= 
.
В результате получим,
что n-ый член
последовательности Фибоначчи имеет вид: fn=
- 
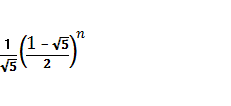(n ϵ
N). (7)
Свойства последовательности Фибоначчи.
1.
f1 + f2 + …+ fn = fn-1 - 1. (8)
Доказательство.
Так как каждый член последовательности, начиная с третьего, равен сумме двух
предыдущих членов, то можем составить следующие равенства: f1 = f3 - f2, f2
= f4 - f3, …, fn-1 = fn+1 -fn, fn = fn+2-fn+1.
Сложив все эти равенства
почленно, получим: f1+f2+…+fn=fn-1- f2, и так как f2=1, получим (8).
2. f1+f3+f5+…+f2n-1 =
f2n.
3. f2+f4+…+f2n=f2n+1-1.
Доказательство.
4. Свойства 2 и 3
доказывается аналогично 1.
5. f12 +
f22+… +
fn2 = fn·fn+1.
(9)
Доказательство.
Имеет место
соотношение: fn·fn+1-fn-1·fn
= fn(fn+1-fn-1) = fn2 (n ϵ
N).
Из этого соотношения
получаем равенства:
f12 = f1·f2, f22 = f2·f3 - f1·f2, f32 = f3·f4 - f2·f3, …, fn2 = fn·fn+1 - fn-1·fn.
Складывая эти равенства
почленно получаем (9).
6. fn+m = fn-1·fm + fn·fm+1. (10)
Доказательство.
Докажем свойство
используя метод математической индукции. Проведем индукцию по m ϵ
N.
Для m = 1, равенство (10)
примет вид: fn+1 = fn-1·f1 + fn·f2, что очевидно. При m=2 формула (10) также
очевидна. Действительно,
fn+2 = fn-1·f2 + fn·f3 = fn+m = fn-1 + 2fn = fn-1 + fn
+ fn = fn+1 + fn.
Таким образом, пусть
основание индукции проверено (m
= 1; m = 2). Пусть (10) верно
для m = k
и для m = k+1.
Докажем, что тогда (10) верно и для m=k+2.
Таким образом, пусть
верны равенства
fn+k = fn-1·fk
+ fn·fk+1, fn+k+1 = fn-1·fk+1 + fn·fk+2.
Суммируя почленно эти
равенства, получим: fn+k+2 = fn-1·fk+2 + fn·fk+3, которое представляет
(10) при m = k + 2.
7. f2n = fn-1·fn + fn·fn+1.
Доказательство следует
из (10) при m = n.
8. Член f2n делится на fn.
Доказательство.
Из 6-го свойства
следует f2n = fn(fn-1 + fn+1), откуда следует, что f2n 
fn.
9. f2n = f2n+1 –f2n-1.
10. f3n =
f2n+1 +
f3n - f3n-1.
Свойства 8-10, являются
следствиями 6 свойства.
11. f2n = fn-1fn+1 + (-1)n+1
(11)
Доказательство.
Будем доказывать
равенство (11) индукцией по n.
При n = 2 равенство (11)
преобразуется в справедливое равенство:
f22 = f1·f3 –
1. Предположим, что равенство (11) справедливо для n и докажем, что тогда оно справедливо и для n+1. Таким образом, пусть
справедливо равенство: f2n = fn-1·fn+1 + (-1)n+1.
Прибавим к обеим частям
последнего равенства fn·fn-1. В результате получим f2n+fn·fn+1 = fn-1·fn+1+ fn·fn+1+(-1)n+1, или fn(fn+fn+1)=fn+1(fn-1+ fn)+(-1)n+1, и так как fn+2=fn+fn+1 (см. определение
последовательность Фибоначчи), заключаем что fnfn+2= fn+12+(-1)n+1, или fn+12= fn·fn+1+(-1)n+2. Следовательно (11)
справедливо и для n+1.
Литература
1.
А.И.
Маркушевич, Возвратные последовательности. - [Текст] / Маркушевич А.И. - Москва, Наука, 1975.
2. Н.Н. Воробьев «Числа Фибоначчи». - [Текст] / Воробьев
Н.Н. Издательство «Наука» 1983г.