УДК: 528 Абжапарова Д.А. (ОшГУ)

Ордобаев Б.С. (КРСУ)

Инженерные основы применения проекции и координат Гаусса-Крюгера в инженерно-геодезических работах в Кыргызской Республики.

Аннотация

В данной статье предлагается один из способов решения вопроса принимаемого проекций Гаусса-Крюгера для решения инженерно-геодезических задач в условиях Кыргызской Республики, а также определяются достоинства и недостатки каждой проекции и связанные с ними системы координат.

DA Abzhaparova (OshSU)

Application of engineering principles and coordinate projection Gauss-Kruger geodetic works in the Kyrgyz Republic.

Annotation

       This article proposes a way of resolving the question of the received Gauss-Kruger projection solutions for geodetic missions in the Kyrgyz Republic, and identifies the advantages and disadvantages of each projection and associated coordinate system.

На сегодняшний день на практике создания геодезического обоснования, для различного рода выполнения инженерно-геодезических работ возникает проблема по привязке съемочной геодезической сети к пунктам государственной сети. В связи с этим возникает трудности по практическому применяемого проекции Гаусса-Крюгера, так как математическая база предлагаемой проекции сложна и громоздка.

Прежде чем приступить к решению этой задачи, рассмотрим современную практику применения проекции и координат Гаусса-Крюгера в инженерных, городских геодезических и маркшейдерских работах. С развитием инженерно-геодезических и городских работ недостатки системы координат Гаусса-Крюгера привели к тому, что ее стали постепенно заменять условными и местными системами прямоугольных координат, которые более или менее отвечали требованиям градостроительной и маркшейдерской практики. Кратко проследим современную практику применения проекции и системы координат в главнейших областях инженерной деятельности, в частности: в инженерно-геологических и геофизических работах, в гидро–энерго-строительстве, в градостроительстве, в промышленном и гражданском строительстве, в горно-маркшейдерских работах [1,8].

При инженерно-геологических и геофизических работах в зависимости от стадий работ пользуются аналитическими данными: координатами, длинами сторон, дирекционными углами, топографическими планами и картами в различных масштабах. Сравнительная относительная точность, порядка 1:1000÷1:1500 производимых геологических и геофизических работ позволят применения исследуемого участка от осевого меридиана -х или 6-ти зоны. Однако, предъявляемые требования к точности инженерно-геодезических и съемочных работ, выполняемых в масштабах 1:2000÷1:500 для инженерной геологической практики коренным образом меняет постановку вопроса о выборе целесообразной проекции.

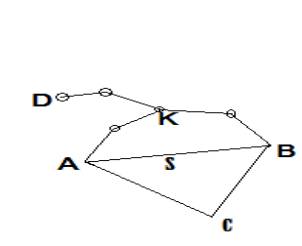
Примем предельную графическую точность топографической съемки для точки D (рис.1), определяемой из геодезической привязки, тогда, следуя рассуждениями А.И.Дурнева (15), среднюю квадратическую ошибку точки К сети сгущения как опорной, в худшем случае нужно иметь в два раза меньшую, чем т.е

= (1)

При соблюдении такого требования в государственной геодезической сети (пункты А,В,С) необходимо иметь точность в 2-3 раза выше, чем точность развиваемой сети сгущения, поскольку она предназначена не только для топографической съемки, но и для целого ряда геодезических измерений, выполняемых для проектных и строительных работ.

Следовательно, (2)

рис.1. Топографической сьемки для точки D

где - средняя квадратическая ошибка в длина стороны триангуляции приравненная к ошибке определения пункта.[10] Таким образом, согласно инструкции для последней ступени съемки в масштабе 1:500 при точности построения топографической основы геологических карт равной 0.3 мм, имеем =0.15м, 0.075м,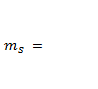 0.038м. Другими словами, самая слабая сторона триангуляции 4 класса длиной 2км должна определяться с относительной ошибкой

= =

Относительная ошибка сети сгущения, проложенной между пунктами триангуляции 4 класса, определяется по формуле

= =

Для съемочного обоснования, при длине теодолитного хода между точками полигонометрии равной 0.5км, получим

= = =

Из этого следует, что если пользоваться численным результатами съемок в проекции Гаусса-Крюгера, то при выносе проектов инженерно-геологических объектов в натуру мы должны d и углы, рассчитанные по координатам, вводить поправки за переход с плоскости на эллипсоид. Это конечно, доставляет большие неудобства в вычислениях. Поэтому, чтобы избежать этого на практике весьма часто пользуются местной системой координат [4].

В гидро-энерго-строительстве в зависимости от стадии проектирования и строительства пользуются материалами топографических съемок масштаба 1:250000÷1:500. Планы масштабов 1:5000÷1:500 выполняются либо в проекции -х зонах, либо в местной системе координат.

В зависимости от вида запроектированного гидротехнического сооружения определяется и рассчитывается точность инженерно-геодезических работ для гидротехнического строительства, которая достаточно высокая и составляет от 20 до 1 мм.

Точность обычных геодезических сетей в таких случаях не всегда удовлетворяет указанному допуску. Поэтому для этих целей используется специальная гидротехническая триангуляция трех разрядов. Особенность ее заключается в том, что при наличии коротких сторон сети, она обеспечивает получение длин сторон, углов и координат с высокой степенью точности[4,10].

Относительная ошибка наиболее слабой стороны гидротехнической триангуляции находится в пределах от 1:70000 до 1:200000. Как показывают результаты исследований точности государственной геодезической сети, приведенные в работе С.Г. Судакова, государственное обоснование не может представить исходных данных для указанной сети специального назначения, и т.к. ошибки этих данных одного порядка с собственно ошибками измерения наиболее ответственных сторон. Следовательно, чтобы не вносить ошибок исходных данных в сети специального назначения государственные геодезические сети должны иметь относительные ошибки слабо определяемых сторон от 1:40000 до 1:400000. Поэтому геодезические сети гидротехнической триангуляции следует создавать на собственных базисах, используя лишь ориентировку направлений и координаты одного из пунктов государственной геодезической сети. Высокоточная гидротехническая геодезическая сеть должна обрабатываться в такой проекции, которая дала бы неощутимые искажения расстояний и редукции углов.

По этой причине вопросы целесообразного выбора поверхности относительно осевого меридиана в гидро-энерго-строительстве имеют большое принципиальное значение.

Так, к примеру, при обработке высокоточной гидротехнической триангуляции 2 разряда, выполненной автором для строительства в Кыргызстане высокогорного Кировского водохранилища, пришлось вообще отказаться от проекции Гаусса-Крюгера, поскольку длина плотины в 257м, вычисленная в ней, на 50мм больше действительной, а отводного туннеля длиной 360м, соответственно на +68мм. По Токтогульской ГЭС соответствующие величины значительно больше.

Естественно, что на практике при использование геодезических данных, если они вычислены в проекции Гаусса-Крюгера, в проектировании и строительстве возникают определенные трудности.

Для проектирования и строительства городов согласно СН-212-62 необходимо иметь топографические карты и планы в масштабе 1:10000 ÷ 1:5000 выполняются обычно в проекции и по координатам Гаусса-Крюгера а остальные либо в условной, либо в местной системе координат [4].

Чтобы обеспечить точность изображаемых предметов городских территорий со сложным надземным и подземным хозяйством в последней стадии съемок в масштабе 1:500, необходимо определять точки съемочных ходов со средней квадратической ошибкой 0.2мм на плане, что соответствует = 0.10 м на местности. Отсюда

= = 0.05 м,

= = 0.025 м.

Тогда относительная ошибка определения слабой стороны городской триангуляции 4 класса при s = 2км должна быть

= =

Относительная ошибка для сети сгущения, проложенной между пунктами триангуляции, равна

= =

Для съемочного обоснования при длине теодолитного хода 0.8 км между точками полигонометрии, при масштабе 1:500 аналогично прежнему получим

Соответственно при длины теодолитного хода d = 500 м, вместо данной в СН – 212- 62 точности 1:2000, относительная ошибка будет

Очевидно, созданное постоянное обоснование такой точности будет достаточным при решении многих инженерно-технических задач градостроительства. Перенесение в натуру проектов планировки и застройки городов производится действием обратным съемке местности. Геодезические разбивочные работы в большинстве случаев по точности в несколько раз выше точности работ, производимых при съемке. Для обеспечения разбивки, а также для контроля ее не обходимо, чтобы положение пунктов разбивочной опорной сети было определено с точностью в 2 раза больше той, которая принята при разбивке сооружений. Поэтому предельная относительная ошибка взаимного положения пунктов плановой опорной сети в последней стадии долина быть соответственно 1:5000, что соответствует 2 разряду по классификации городской полигонометрии [7].

Созданное плановое обоснование такой точности в системе координат Гаусса-Крюгера во многих случаях практики городских работ потребует обратного перехода к натуральным значениям длин сторон и углов. В противном случае, при выполнении инженерно-геодезических работ с относительной ошибкой выше 1:2500 для разбивки уникальных сооружений и коммуникаций потребуются специальные локальные сети ограниченного распространения, или на собственных базисах, измеренных с высокой степенью точности без введения каких-либо поправок в длины сторон и углов.

Для осуществления проектно-планировочных работ по промышленному и гражданскому строительству должно быть заранее подготовлены топографические планы и геодезические данные, служащие основой для проектирования. Топографическая основа необходима для правильного размещения объектов, планировки и застройки.

В соответствии с принятыми инструкциями, нормами и правилами по планировке и застройке промышленных и гражданских сооружений возникают необходимость иметь топографические планы и карты для различных видов и стадий проектирования в масштабах 1:200; 1:500; 1:1000; 1:2000; 1:5000; 1:10000.

Геодезические съемки территорий промышленных предприятий, за исключением специальных объектов, по методу выполнения близкими к городским крупномасштабным. Следовательно, точность триангуляции, полигонометрии и сетей сгущения для крупномасштабных съемок включительно до 1:500 остаются одинаковыми и рассчитываемыми для градостроительства. Относительные невязки теодолитных ходов не должны превышать 1:2500 при максимальной длине хода 0.5 км

Однако и современных методах строительства из сборных конструкций и элементов требуется наибольшая точность при разбивке зданий по сравнению с точностью разбивки кирпичных сооружений. В связи с этим, требования промышленного и гражданского строительства к инженерно-геодезическим работам увеличиваются и, как следствие этого, чаще возникает потребность в создании специального высокоточного геодезического обоснования. Поэтому многие проектные и строительные организации пользуются топографическими планами масштабов 1 : 2000÷1 : 500 и аналитическими данными в условной или местной системах координат, так как размеры крупных сооружений длиной более 1 км, вынесенные в натуру по геодезическому обоснованию в проекции Гаусса-Крюгера, на краю -х зон увеличиваются до 20 см, что значительно превышает технические допуски в строительстве [6].

Из различного рода карт наибольшее значение для горного дела имеют топографические карты масштабов 1:25000; 1: 10000. Основными маркшейдерскими планами горных работ для различного вида горно-промышленных предприятий считаются планы в масштабах 1:5000÷1 : 500. В этой отрасли народного хозяйства гораздо чаще, чем в других из-за отсутствия исходных данных и значительных искажений проекции Гаусса-Крюгера, применяется условная система координат, приведенная к средней уровненной поверхности участка горных работ.

Так к примеру, если использовать плановое обоснование для автодорожного туннеля Тоо-Ашуу по трассе Бишкек – Ош длиной 2370 м в проекции Гаусса-Крюгера , то для края - й зоны ( 120 км) под широтой , получим

= S = S = 0.474 м

А если учесть широкий размах горно-маркшейдерских работ (например, туннель Тоо-Ашуу по трассе Бишкек-Ош длиной 2370 м), то станет ясным и вопрос несоответствия между точностью специального обоснования и искажениями проекции.

Согласно требованиям, предъявляемым к строительству и эксплуатации горных предприятий устанавливается классификация локальных геодезическо-маркшейдерских сетей по типу гидротехнической триангуляции с относительной ошибкой слабо определяемой стороны 1 : 70 000÷1:200 000. Подобная триангуляция, создаваемая для контроля неподвижности пунктов, от которых ведутся наблюдения за горизонтальными и вертикальными смещениями сооружений, должна обеспечивать положения этих пунктов со средней квадратической ошибкой не более . Допуски смещений сооружений рассчитываются в зависимости от ожидаемых величин оседаний и горизонтальных сдвигов [5,8].

В итоге вышеизложенного можно сделать следующие выводы и предложения:

1. Проекция должна быть камфорная, причем линейные искажения и редукция направлений в ней возможно малые искажения.

2. Система координат должна иметь единую схему применения для всех городских и инженерно-геодезических работ.

3. Она математически должна быть связана с общегосударственной системой координат и легко определяемой в последнюю.

Литература

1. Христов В.К. Координаты Гаусса-Крюгера на эллипсоде вращения. - М.: Геодезиста, 1957. – 203 с.

2. Болшаков В.Д. Практикум по теории математической обработки годезических измерений. – М .: Недра, 1983. – 223 с.

3. Куштин И.Ф., Куштин В.И. Геодезия: учебно-практической пособие- Ростов н/Д: Феникс, 2009. – 909 c.

4. Зенин В.Н. разработка специальной геодезической проекции для инженерных и городских геодезических работ// Автореферат диссертации на соискание ученной степени кандидата технических наук. – М.: 1970. – 12 с.

5. Голубев В.В. Теория математической обработки геодезических измерений. – М.: Недра, 2009. – 2 46 с.

6. Бойко Е.Г. Высшая геодезия // Часть II. Сфероидическая геодезия – Картгеоцентр. – М.: Геодезиздат, 2003. – 144 с.

7. Огородова Л.В. Высшая геодезия // Часть III. Теоретическая геодезия. – М.: Геодезкартиздат, 2006. – 245 с.

8. Яковлев Н.В. Высшая геодезия. – М.: Недра, 1989. – 445 с.

9. Пеллинен Л.П. Высшая геодезия. – М.: Недра, 1978. – 264 с.

10. Бессель Ф.В. Высшая геодезия и способ наименьших квадратов. – М.: Геодезлитиздат, 1961. – 282 с.

11. Карабцова З.М. Геодезия. – М.: Издательство Дальневосточного университета, 2002. – 153 с.

1. Абжапарова Динара Амалбековна – старший преподаватель ОшГУ;

Номер мобильного телефона +996559901350;

Номер рабочего телефона (+996 03222) 5 46 65;

Электронная почта: ada23121970@yandex.ru.

2. Ордобаев Бейшенбек Сыдыкбекович – к.т.н., профессор, зав. кафедрой «ЗЧС» КРСУ и МЧС КР;

Номер мобильного телефона +996550127840;

Номер рабочего телефона +996312895154;

Электронная почта: ordobaev@mail.ru.