Технические науки/10.Горное дело

К.т.н. Каражанов А.А.

Таразский государственный университет имени М.Х.Дулати,

Республика Казахстан

Конструирование криволинейной поверхности туннелей по заданным требованиям

Теория конструирования криволинейных каркасных поверхностей с применением аффинных и проективных преобразований разработана в научных работах профессора Котова И.И.[3].

В данной статье эти направления исследования получило некоторое развитие с использованием (2-2)-значного геометрического преобразования Г₂ с вертикальной осью симметрии.

Метод конструирования криволинейной поверхности туннелей с применением геометрического преобразования Г₂ заключается в следующем:

1. задается каркас поперечных сечений поверхности туннелей. Например, пусть будут заданы 4 поперечные сечения рассматриваемого туннеля (рисунок 1);

2. моделируем геометрическую форму и определяем уравнение первого сечения поверхности туннеля с использованием геометрического преобразования Г₂ (см. раздел 3.1). При этом получим значение R₁ параметра R преобразования Г₂ и значение a₁, c₁, d₁ параметров a, c, d прообраза-эллипса (рисунок 2);

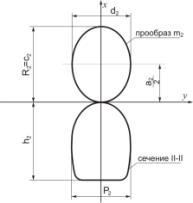
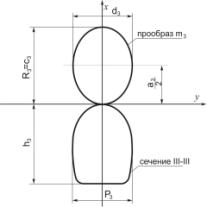
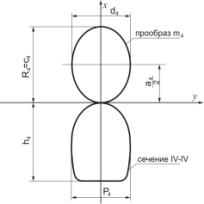
3. аналогичным образом определяем параметры R₂, a₂, c₂, d₂, R₃, a₃, c₃, d₃, R₄, a₄, c₄, d₄ соответственно для 2-го, 3-го и 4-го сечения поверхности туннеля (рисунки 3 – 5);

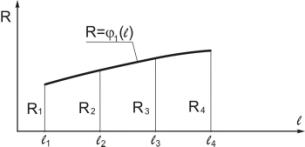
4. интерполировав значения R₁, R₂, R₃, R₄ параметра R по длине туннеля (рисунок 6), получим закономерность плавного изменения параметра R по длине туннеля:

. (1)

5. аналогичным образом определяем закономерности плавного изменения параметров a, c, d поперечного сечения по длине туннеля:

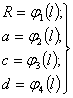, (2)

где R, a, c, d - параметры поперечного сечения туннеля

(рисунки 7 – 9);

φ₁, φ₂, φ₃, φ₄ - непрерывные функции;

- длина туннеля, 0≤≤.

6. используя формулы (2), записываем уравнение поверхности туннеля в виде:

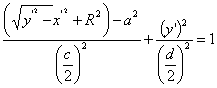, (3)

где R=φ₁();

a=φ₂ ();

c=φ₃ ();

d=φ₄ ();

0≤≤;

- длина рассматриваемого участка туннеля.

7. для моделирования произвольного поперечного сечения поверхности туннеля:

а) задается длина по оси туннеля:

= . (4)

б) для определяем R⁰, a⁰, c⁰, d⁰ значения параметров R, a, c, d используя уравнение (2) и эти значения подставим в уравнение (3);

в) после этого можно вычертить контур требуемого поперечного сечения поверхности туннеля, используя прикладную программу.

Таким образом, применение геометрического преобразования Г₂ позволяет конструировать новые виды кривых поверхностей туннелей.

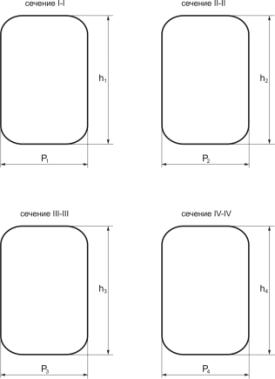
Рисунок 1 - Поперечные сечения рассматриваемого туннеля

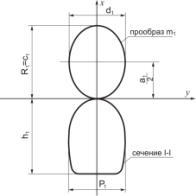
Рисунок 2 - Определение значений параметров R₁, c₁, a₁, d₁

Рисунок 3 - Определение значений параметров R₂, c₂, a₂, d₂

Рисунок 4 - Определение значений параметров R₃, c₃, a₃, d₃

Рисунок 5 - Определение значений параметров R₄, c₄, a₄, d₄

Рисунок 6 - Закономерность изменения параметра R

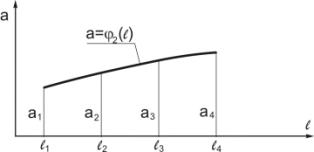
Рисунок 7 - Закономерность изменения параметра a

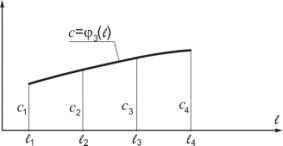
Рисунок 8 - Закономерность изменения параметра c

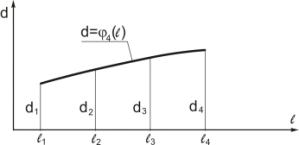
Рисунок 9 - Закономерность изменения параметра d

Литература

1. Джапаридзе И.С. Геометрические преобразования пространства и их применения в начертательной геометрии. Методы начертательной геометрии и ее приложения. – М.:1955 – 54-222 с.

2. Конакбаев К.К. Конструирование обводов из дуг уникурсальных циркулярных кривых посредством кремоновых инволюций. автореф. ...канд.техн.наук: 05.150. – М.: МТИПП, 1972 – 18 с.

3. Котов И.И. Алгоритмы конструирования каркасных поверхностей. – М.: МАИ, 1975.