Технические науки/ 5.Энергетика

Аспирант Коротков М.Ф.

Сибирский Федеральный университет Политехнический институт, Россия

К.т.н. Пахомов А.Н.

Сибирский Федеральный университет Политехнический институт, Россия

Модальные регуляторы замкнутой системы трехфазного асинхронного электропривода

В системах электропривода переменного тока широко используют полупроводниковые преобразователи частоты с инверторами напряжения. Для достижения высокого качества электрической энергии на выходе таких преобразователей применяют различные виды широтно-импульсной модуляции. Снабдив систему преобразователь частоты с автономным инвертором напряжения с широтно-импульсной модуляцией (ПЧ с АИН с ШИМ) – асинхронный двигатель (АД) модальным регулятором, построенным на основе суммирования обратных связей по вектору состояния, возможно обеспечить предельное быстродействие и точность в динамических режимах работы.

Рассмотрим порядок синтеза модального регулятора системы ПЧ с АИН с ШИМ – АД. Расчет коэффициентов модального регулятора и проверка работы системы производится в несколько этапов. В дополнение к [4] настоящая работа позволяет исследовать замкнутую систему с моделью ПЧ с АИН с ШИМ вместо статического коэффициента передачи .

1. Построение математической модели объекта управления. За основу взята математическая модель АД с учетом общепринятых допущений [2, 3] в декартовой системе координат u-v, вращающейся с произвольной скоростью . Системы уравнений приведены в [4].

Синтез модального регулятора производится для двух контуров регулирования: потокосцепления и скорости ротора АД. Используем систему координат u-v, вращающуюся со скоростью вращения магнитного поля и ориентированную по вектору потокосцепления ротора. Матрицы динамики и входа канала регулирования потокосцепления ротора, для обоих каналов регулирования приведены в [4].

В матрице входа используется коэффициент передачи ПЧ АИН с ШИМ , который определяется отношением амплитуд основной гармоники выходного напряжения АИН и выходного сигнала регулятора.

2. Расчет модальных регуляторов. Синтез регуляторов производится отдельно для двух каналов управления: канала регулирования потокосцепления ротора АД и канала регулирования скорости АД.

Определение коэффициентов модального регулятора выполняется методом стандартных уравнений в нормированной форме [1]. Векторы коэффициентов модального регулятора (; ) и (; ) для обоих каналов регулирования приведены в [4].

3. Имитационное моделирование замкнутой системы электропривода. Эффективность методики синтеза модальных регуляторов проверяется при помощи пакета имитационного моделирования Matlab фирмы The MathWorks, Inc. На рис. 2 приведена структурная схема замкнутой системы асинхронного электропривода во вращающейся со скоростью магнитного поля системе координат.

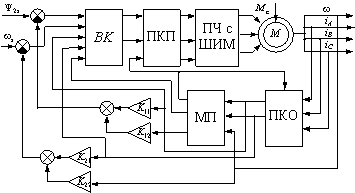
Рисунок 2 – Структурная схема

В структурной схеме приняты следующие обозначения: M – модель трехфазного АД; BK – блок компенсаций перекрестных связей по току статора; и – заданные значения потокосцепления и скорости ротора АД; – коэффициенты модального регулятора; , – скорость, электромагнитный момент, потокосцепление ротора АД; ПКП, ПКО - преобразователи координат прямого и обратного каналов; МП - модель потока.

МП описывается следующими уравнениями:

, .

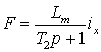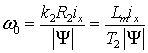На рис. 3 и 4 изображены графики переходных процессов токов статора АД в исследуемой замкнутой системе (рис. 2) для двух вариантов модели ПЧ. Рис. 3 иллюстрирует работу системы, в которой модель ПЧ заменена линейным коэффициентом передачи. При использовании модели ПЧ с АИН с ШИМ появляются пульсации тока статора (рис. 4), но их величина незначительна, что позволяет использовать коэффициент в качестве математического описания ПЧ для расчета модальных регуляторов.

На рис. 5 изображены графики переходных процессов в исследуемой модели с учетом модели ПЧ с АИН с ШИМ. Сначала подается задание на потокосцепление ротора АД, которое успешно отрабатывает канал регулирования потокосцепления, после чего производится скачек задания на скорость вращения ротора и включается в работу второй канал. И, наконец, на третьем участке осуществляется моделирование наброса нагрузки на валу АД.

Характер переходных процессов соответствует заданным настройкам. Модальные регуляторы двух подсистем регулирования координат АД позволяют обеспечить требуемый уровень потокосцепления ротора и скорости АД с заданным быстродействием.

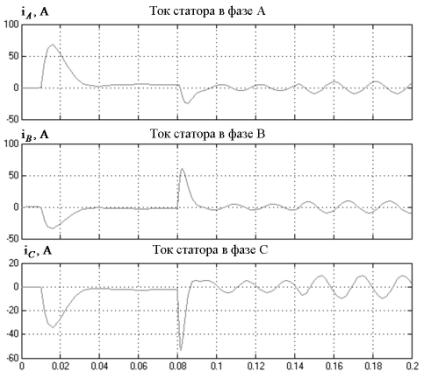
Рисунок 3 – Графики переходных процессов токов статора. Вместо модели ПЧ с АИН с ШИМ статический коэффициент

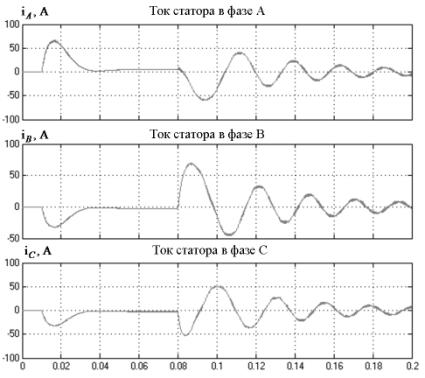
Рисунок 4 – Графики переходных процессов токов статора, с учетом модели ПЧ с АИН с ШИМ

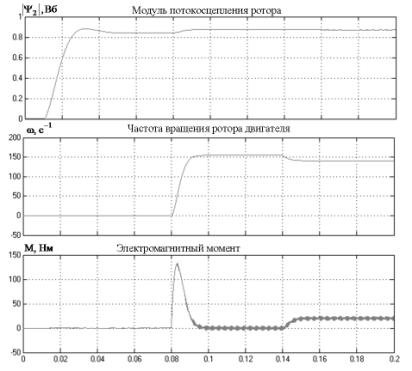
Рисунок 5 – Графики переходных процессов

Следует отметить, что в графике момента присутствуют пульсации, обусловленные наличием ШИМ в ПЧ. Однако их величина незначительна, что позволяет проектировать и исследовать замкнутую систему на уровне гладкой составляющей кривых переходных процессов.

Основным результатом работы является подтверждение возможности использования коэффициента передачи по напряжению ПЧ для синтеза модальных регуляторов системы асинхронного электропривода.

Литература:

1. Терехов В. М. Системы управления электроприводов: Учебник для студ. высш. учеб. заведений / В. М. Терехов, О. И. Осипов; Под ред. В. М. Терехова. – М.: Издательский центр «Академия», 2005. – 304 с.

2. Соколовский Г. Г. Электроприводы переменного тока с частотным регулированием: учебник для студ. высш. учеб. Заведений / Г. Г. Соколовский. – М.: Издательский центр «Академия», 2006. – 272 с.

3. Карагодин М. С. Уравнения динамики частотно-управляемых электроприводов: учеб. пособие / М. С. Карагодин, А. А. Федоренко. – КрПИ: Красноярск, 1985. – 92 с.

4. Коротков, М. Ф. Методика проектирования модального регулятора векторной системы асинхронного электропривода / М. Ф. Коротков, А. Н. Пахомов // Современные техника и технологии: сборник трудов XVII Международной научно-практической конференции студентов, аспирантов и молодых ученых. В 3 т. Т. 1 / Томский политехнический университет. – Томск: Изд-во Томского политехнического университета, 2011. - 581 c.