Ïèëü Ý.À.
Àêàäåìèê ÐÀÅ, ä.ò.í., ïðîôåññîð
THEORY OF THE FINANCIAL CRISES (PART IV)
Earlier in his articles the author has shown that in
order to describe the economic processes that occur in the economy of a country
it is possible to apply the shell theory, in its application to the spheres [1,
4]. Besides, the author has also described in the articles the boundaries of
existence of economic shells of small-, medium- and big-sized businesses which
may be influenced by both external and internal forces [2, 3]. The author
suggests in the following article to employ shell, and, to be more specific - its surface which will make it possible to use six different variables
during calculation of the GDP.
Gross domestic product (GDP) can be calculated by the
three following methods:
1.
as the sum of gross value added (production method);
2.
as the sum of end-use components (end-use method);
3.
as the sum of primary income (distribution method).
In this case the various variables may be used in the
calculation, in particular such as: consuming capacity, investments,
governmental expenditures, exports, imports and the like. In the material
presented below the calculation formula of surface of the economic shell Seu was used, to which
corresponds the GDP of the country, that is Seu
(GDPeu) = f(Õ1, Õ2,
Õ3, Õ4, Õ5, Õ6). Here Õ1, Õ2, Õ3,
Õ4, Õ5 and Õ6 are the variables which have an impact on the GDP of the country.
By analysing the formula it is possible to identify
the variables' characteristics which influence on the Seu (GDPeu),
and which will be as follows:
·
where the Õ1
variable is increased, the economic shell surface Seu GDPeu
increases too
·
where the Õ2
variable is increased, the economic shell surface Seu (GDPeu)
increases more profoundly compared to the increase of variable X1;
·
where the Õ3
variable is increased, the economic shell surface Seu (GDPeu)
decreases;
·
where the Õ4
variable is increased, the economic shell surface Seu (GDPeu)
increases. In such a case the X4 variable may approach to numeral one only
asymptotically;
·
where the Õ5
variable is increased, the economic shell surface Seu (GDPeu)
decreases;
·
where the Õ6
variable is increased, the economic shell surface Seu (GDPeu)
increases less profoundly compared to the increase of variable X4. In such a
case the X6 variable may approach to numeral one only asymptotically.
It should immediately be noted that during calculation
and plotting of construction drawings, the parameters Õ1,
Õ2, Õ3, Õ4, Õ5 and Õ6 could be constant values, increase or decrease by 10 times. On the basis
of the calculations made, 82 graphics were built, which can be divided into the
four following groups:
parameter values Õ1, Õ2, Õ3, Õ4, Õ5
and Õ6
increase and are constant;
parameter values Õ1, Õ2, Õ3, Õ4, Õ5
and Õ6
decrease and are constant;
parameter values Õ1, Õ2, Õ3, Õ4, Õ5
and Õ6
decrease and increase;
parameter values Õ1, Õ2, Õ3, Õ4, Õ5
and Õ6
are constant, they decrease and increase.
It is worth mentioning here in this context that the
number of the graphs that may be plotted with the six variables is
significantly greater. Therefore the author has selected such options of the
variables' values which will more precisely show the variables' influence onto
the GDP calculation.
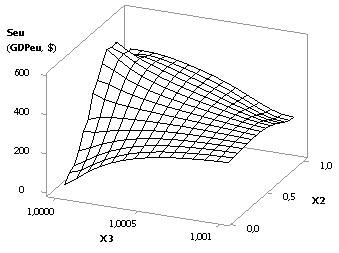
Figure 1 shows the 2D graph of Seu (GDPeu)
dependency with Õ1 = 1, Õ2 = Õ3 = Õ5 = 1
10, Õ4 = Õ6 = 0.1
0.99 from which it is
clear that the Seu values
initially decrease by 5.07 times, and afterwards increase by 3.58 times. The
minimal value of the Seu
(GDPeu) falls on point 7,
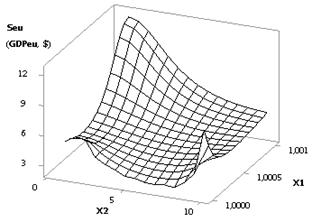
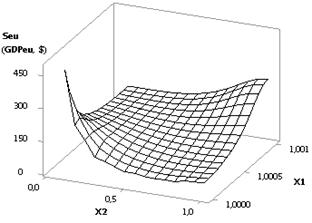
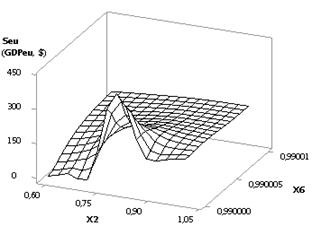
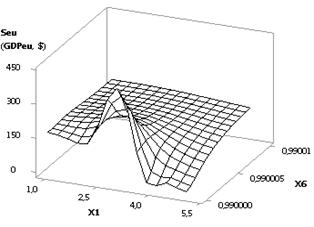
and is equal to 2.44. Figure 2 shows two 3D-graphs which give the possibility
to more illustratively present the changes in the Seu. In this particular case it is essential to have the
values of the extreme points, since with such values the Seu value, and finally the GDPeu, will be maximal.
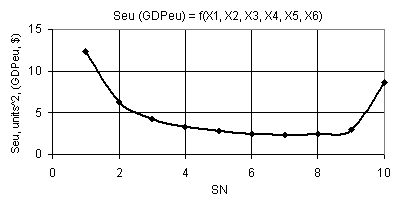
Fig. 1. Dependence Seu (GDPeu) = f(Õ1, Õ2, Õ3,
Õ4, Õ5, Õ6)
when Õ1 = 1, Õ2 = Õ3 = Õ5 = 1
10, Õ4 = Õ6 =
0.1
0.99
|
a |
b |
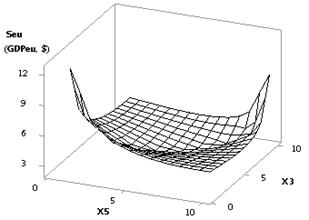
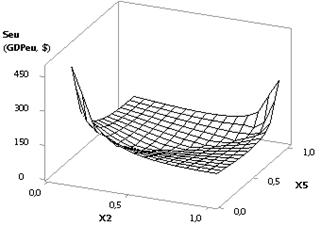
Fig. 2. 3D-graphics: a - Seu (GDPeu) = f(Õ2, Õ1); b - Seu (GDPeu) = f(Õ5, Õ3)
when Õ1 = 1, Õ2 = Õ3 = Õ5 = 1
10, Õ4 = Õ6 = 0,1
0.99
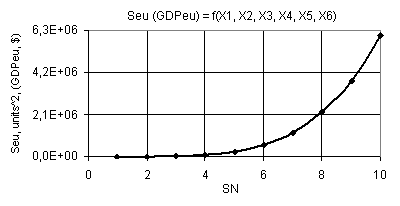
Fig. 3. Dependence Seu (GDPeu) = f(Õ1, Õ2, Õ3, Õ4, Õ5, Õ6)
when Õ1 = Õ2 = 1
10, Õ3 = Õ5 = 1, Õ4 = Õ6 =
0.99
|
a |
b |
Fig. 4.
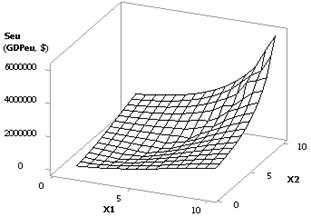
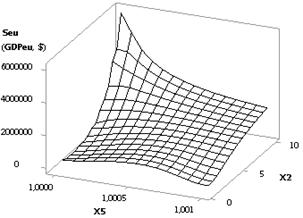
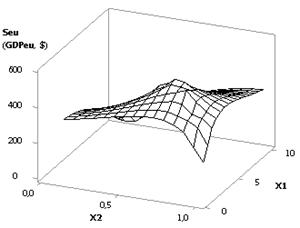
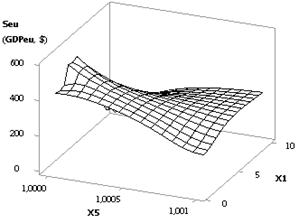
3D-graphics: a - Seu (GDPeu) = f(Õ1, Õ2); b - Seu (GDPeu) = f(Õ5, Õ2)
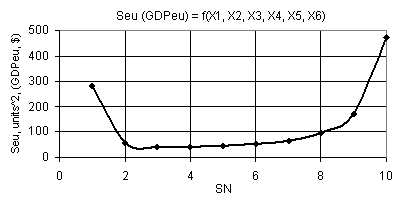
Fig.
5. Dependence Seu (GDPeu) = f(Õ1, Õ2, Õ3, Õ4, Õ5, Õ6)
when Õ1 = 1, Õ2 = Õ3 = Õ5 = 1
0.1, Õ4 = Õ6
= 0.99
0.1
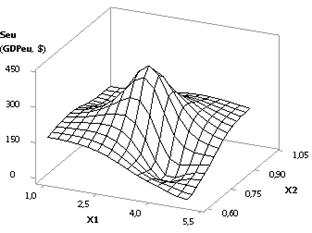
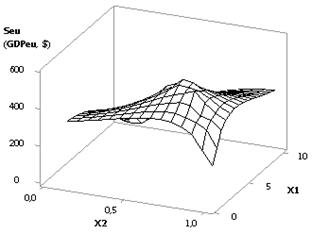
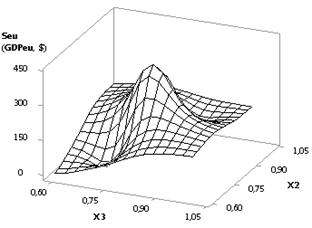
From the next Figure 3 it is clear that when Õ1 = Õ2 = 1
10, Õ3 = Õ5 = 1, Õ4 = Õ6 = 0.99 the plotted curve Seu grows in full swing from
the value 194,89 up to 6.03Å+06, that is - it increases by 30944.44 times. Figure 4 shows two types of the present
dependency in way of 3D-graphs. Such option is the most preferred one, since
the biggest increase of the values Seu (GDPeu)
takes place under the influence of external forces.
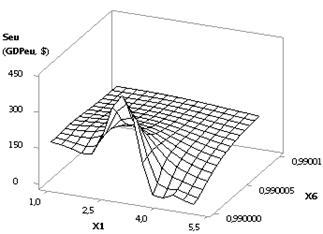
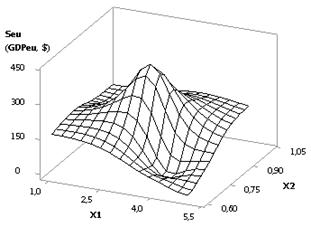
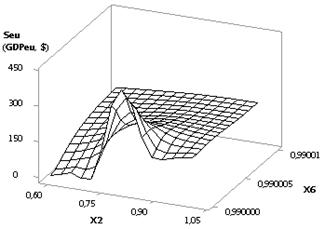
In Figure 5 we may see that the Seu curve plotted has also the minimum of 42.56 in
point 4, after which its values increase. This figure was plotted under the
following values of the variables: Õ1 = 1, Õ2 = Õ3 = Õ5 = 1
0.1, Õ4 = Õ6 = 0.99
0.1. Here, it is also important to select the variables in extreme points,
since in this case the economy of the country in question will have the maximal
values of the Seu. The depicted Seu curve plotted in Figure 5 is presented by two
3D-graphs in Figure 6.
|
a |
b |
Fig. 6. 3D-graphics: a - Seu (GDPeu) = f(Õ2, Õ1); b - Seu (GDPeu) = f(Õ2, Õ5)
when Õ1 = 1, Õ2 = Õ3 = Õ5 = 1
0.1, Õ4 = Õ6
= 0.99
0.1
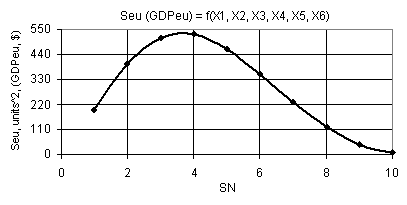
Fig.
7. Dependence Seu (GDPeu) = f(Õ1, Õ2, Õ3, Õ4, Õ5, Õ6)
when Õ1 =
1
10, Õ2 = 1
0.1, Õ3 = Õ5 = 1, Õ4 = Õ6 = 0.99
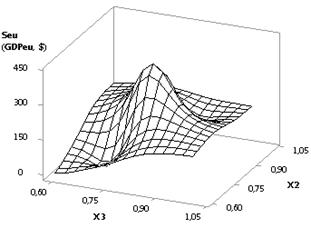
Figure 7 depicts the Seu curve which has its maximum of 261.41 in point 4.
Consequently, use of the following values of variables Õ1 = 1
10, Õ2 = 1
0.1, Õ3 = Õ5 = 1, Õ4 = Õ6 = 0.99 is quite expedient at
the values which are close to the maximal ones. Figure 8 shows three examples
of 3-dimensional surfaces Seu
(GDPeu) = f(Õ1, Õ2,
Õ3, Õ4, Õ5, Õ6).
As it is clear from Figure 9, here the Seu values have their minimum
of 80.18 in point 2, after which they grow up to 407.26, and then drop down to
zero, since the Seu
calculations have no solutions with the subsequent values of the variables.
During plotting of Figures 9 and 10 the following variables were used: Õ1 = 1
10, Õ2 = Õ3 = Õ5 = 1
0.1, Õ4 = 0.99
0.1, Õ6 = 0.99. Here, the four types of
3D-graphs are shown, which are presented in Figure 10.
|
a |
b |
|
c |
|
Fig. 8. 3D-graphics: a - Seu (GDPeu) = f(Õ2, Õ1); b - Seu (GDPeu) = f(Õ5, Õ1)
c - Seu (GDPeu) = f(Õ3, Õ2)
when Õ1 =
1
10, Õ2 = 1
0.1, Õ3 = Õ5 = 1, Õ4 = Õ6 = 0.99
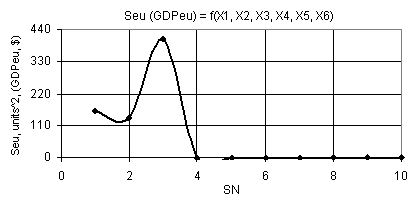
Fig.
9. Dependence Seu (GDPeu) = f(Õ1, Õ2, Õ3, Õ4, Õ5, Õ6)
when Õ1 = 1
10, Õ2 = Õ3 = Õ5 = 1
0.1, Õ4 = 0.99
0.1, Õ6 = 0.99
|
|
|
|
|
d |
Fig. 10. 3D-graphics: a - Seu (GDPeu) = f(Õ1, Õ2); b - Seu (GDPeu) = f(Õ1, Õ6);
c - Seu
(GDPeu) = f(Õ3, Õ2); d - Seu (GDPeu) = f(Õ2, Õ6);
when Õ1 = 1
10, Õ2 = Õ3 = Õ5 = 1
0,1, Õ4 = 0,99
0,1, Õ6 = 0,99
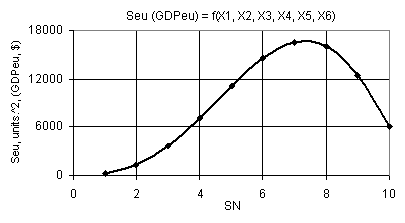
Fig.
11. Dependence Seu (GDPeu) = f(Õ1, Õ2, Õ3, Õ4, Õ5, Õ6)
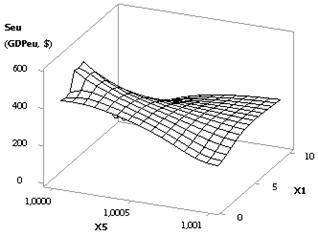
From the following Figure 11 it is obvious that the
plotted Seu-curve has its
maximal value of Seu = 16552.23
in point 7. This particular Figure was plotted with Õ1 = 1
0.1, Õ2 = 1
10, Õ3 = Õ5 = 1, Õ4 = Õ6 = 0.99. The two Figures 12 show
the way how the presented Seu-curve
changes in the three-dimensional space.
|
|
|
Fig. 12. 3D-graphics: a - Seu (GDPeu) = f(Õ3, Õ1); b - Seu (GDPeu) = f(Õ5, Õ2)
when Õ1 = 1
0.1, Õ2 = 1
10, Õ3 = Õ5 = 1, Õ4 = Õ6 = 0.99
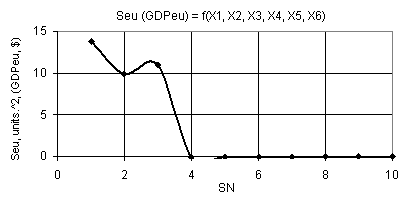
Fig.
13. Dependence Seu (GDPeu) = f(Õ1, Õ2, Õ3,
Õ4, Õ5, Õ6)
when Õ1 = 1, Õ2 = Õ5 = 1
0.1, Õ3 = 1
10, Õ4 = 0.1
0.99, Õ6 = 0.99
The following Figure 13
represents the Seu (GDPeu) curve when Õ1 = 1, Õ2 = Õ5 = 1
0.1, Õ3 = 1
10, Õ4 = 0,1
0.99, Õ6 = 0.99. From this 2D-graph it is seen that the
plotted curve has its minimum of 9.88 in point 2, after which is gets its
maximum of 10.93 in point 3, and next their values drop down to zero. The last
Figure 14 displays the four types of three-dimensional surfaces Seu (GDPeu) for the curve plotted in Figure 13.
After the calculations were completed, their results
were combined into the summary table, which gave totally 110 lines, in spite of
the fact that only 82 two-dimensional graphs have been plotted. This resulted
from the fact that a number of the plotted graphs had their maximums and
minimums. The relationships were introduced into this summary table as the
following:
·
Seub
Seuf, where Seub -
is the initial surface value of financial shell, unit2; Seuf
- is the final value of the surface of financial shell, unit2;
·
Seuf/Seub- is the relation of financial shell final surface value to its initial surface.
|
a |
b |
|
c |
d |
Fig. 14. 3D-graphics: a - Seu (GDPeu) = f(Õ1, Õ2); b - Seu (GDPeu) = f(Õ1, Õ6);
c - Seu (GDPeu) = f(Õ3, Õ2); d - Seu (GDPeu) = f(Õ2, Õ6);
when Õ1 = 1, Õ2 = 1
0.1, Õ3 = 1
10, Õ4 = 0.1
0.99, Õ5 = 1
0.1,
Õ6 = 0.99
The ratio of finite surface of the economic shell Seuf
to the initial Seub shows by how many times the surface of the
economic shell increased (decreased), that is Seu (GDPeu),
under the influence of various external forces onto the one. Hence, by
obtaining these data we may choose such values of variables Õ1, Õ2, Õ3, Õ4, Õ5 and Õ6, with which the surface
of the economic shell remains invariable, or even grows further under influence
of external forces. This means that in case of economical crisis, the selected
values of the variables will make it possible to stay on the previous level, or
even to increase the GDP of the country. After the Table had been plotted with
its 110 lines available, it was converted in the following way, by having left
only those values where Seuf/Seub ≥ 1.
On the basis of such conversion the final table had been obtained, which contained
63 lines, which then was shortened down to 40 lines where the values of the
ratio Seuf/Seub
in column 8 were located in descending order (refer to Table 1). As it is seen
from the calculated data in Table 1 the ratios Seuf/Seub
start with 53166.38 and end up with 1.0. This indicates that for the
example in question the economy may maximally increase even under the pressure
onto the ellipsoidal economic shell as by 53166.38 times, as compared to the
initial state with the following values of the variables, being Õ1 = 1, Õ2 = 1
10, Õ3 = Õ5 = 1
0.1, Õ4 = Õ6 = 0.99
0.1.. Yet maximal
growth of the economic shell will take place in this particular case with 1.0
at Õ1 = 1, Õ2 = Õ3 = 1
0.1, Õ4 = 0.1
0.99, Õ5 = 1
10, Õ6 = 0.99.
The next Table 2 was plotted on the basis of Table 1
in which the data obtained were split into groups by the number of variables
used. As it is seen from Table 2 the data presented in it were grouped into 6
groups, starting from the group with one variable, and ending up with the group
where all the variables were used. It is also seen from this table that the
biggest group was presented by the group containing four variables.
Due to the fact that variable X2
characterises the thickness of the economic shell it means that if it was
accepted as the single unit (Õ2 = 1) then Table 2 will change into Table 3 where
there will be only 20 lines instead of 40. The X2 variable may be characterized
as the ratio of national currency exchange rate to a currency used in
international settlements (US dollar, Euro, etc.).
As a result the following conclusions may be made:
1.
Utilization of different
values of the variables makes it feasible to increase the GDP of the country,
and in a number of instances to increase quite significantly and to lift the
economy out of crisis;
2.
During selection of the
variables' values it is necessary to select such group in which the number of
variables under consideration is minimal;
3.
During selection of the
variables' values it is necessary to select such variables which are less
subject to changes.
|
Table 1. Statistics
of theoretical relation Seuf /Seub, where Seuf
/Seub ≥ 1 in descending order |
||||||||
|
No.
in sequence |
Õ1 |
Õ2 |
Õ3 |
Õ4 |
Õ5 |
Õ6 |
Seub
Seuf.
åä.2 (GDÐeub
GDÐeuf. $) |
Seuf / Seub (GDÐeuf / GDÐeub) |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1. |
1 |
1
10 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
281.61
1.50Å+07 |
53166.38 |
|
2. |
1
10 |
1
10 |
1
0.1 |
0.99
0.1 |
1 |
0.99 |
194.89
1.02Å+07 |
52231.12 |
|
3. |
1
10 |
1
10 |
1 |
0.99 |
1 |
0.99 |
194.89
6.03Å+06 |
30944.36 |
|
4. |
1 |
1
10 |
1
0.1 |
0.99 |
1 |
0.99 |
194.89
6.03Å+06 |
30944.36 |
|
5. |
1 |
1
10 |
1
0.1 |
0.1
0.99 |
1 |
0.99 |
14.36
1.91Å+05 |
13280.39 |
|
6. |
1 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
79.16
4.73Å+05 |
5980.97 |
|
7. |
1 |
1 |
1
10 |
0.1
0.99 |
1
0.1 |
0.99
0.1 |
7.09
8871.41 |
1250.53 |
|
8. |
1 |
1 |
1 |
0.99 |
1
0.1 |
0.99
0.1 |
281.61
280504.87 |
996.10 |
|
9. |
1 |
1
10 |
1 |
0.99 |
1 |
0.99 |
194.89
1.91Å+05
|
978.57 |
|
10. |
1
10 |
1
10 |
1
10 |
0.99 |
1 |
0.99 |
194.89
1.91Å+05 |
978.57 |
|
11. |
1 |
1
10 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
142.99
99734.86 |
697.47 |
|
12. |
1
10 |
1 |
1
10 |
0.1
0.99 |
1 |
0.99 |
14.36
6034.81 |
420.24 |
|
13. |
1 |
1 |
1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
61.96
14973.34 |
241.67 |
|
14. |
1 |
1 |
1
0.1 |
0.1
0.99 |
1
0.1 |
0.1
0.99 |
8.65
1467.03 |
169.68 |
|
15. |
1 |
1
10 |
1
0.1 |
0.1
0.99 |
1
0.1 |
0.99 |
13.77
2090.08 |
151.83 |
|
16. |
1
10 |
1
0.1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
162.05
14973.34 |
92.40 |
|
17. |
1
10 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
177.83
6787.10 |
68.36 |
|
18. |
1 |
1 |
1 |
0.1
0.99 |
1
0.1 |
0.1
0.99 |
8.65
519.37 |
60.07 |
|
19. |
1
10 |
1
10 |
1
10 |
0.99
0.1 |
1 |
0.99 |
194.89
10183.31 |
52.25 |
|
20. |
1 |
1 |
1 |
0.99 |
1
0.1 |
0.1
0.99 |
142.99
7059.34 |
49.37 |
|
21. |
1 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
41.74
1307.04 |
31.31 |
|
22. |
1
10 |
1 |
1 |
0.99 |
1 |
0.99 |
194.89
6034.81 |
30.97 |
|
23. |
1 |
1
10 |
1
10 |
0.99 |
1 |
0.99 |
194.89
6034.81 |
30.97 |
|
24. |
1
10 |
1 |
1
10 |
0.1
0.99 |
1
0.1 |
0.99 |
13.77
292.55 |
21.25 |
|
25. |
1
10 |
1
0.1 |
1
0.1 |
0.1
0.99 |
1 |
0.99 |
14.36
194.89 |
13.57 |
|
26. |
1 |
1 |
1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
35.09
462.80 |
13.19 |
|
27. |
1 |
1
10 |
1
0.1 |
0.99
0.1 |
1
10 |
0.99 |
14.62
137.21 |
9.38 |
|
28. |
1
10 |
1
0.1 |
1
0.1 |
0.99 |
1 |
0.99 |
194.89
995.1 |
5.11 |
|
29. |
1 |
1 |
1
10 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
6.84
32.49 |
4.75 |
|
30. |
1 |
1 |
1 |
0.1
0.99 |
1
0.1 |
0.99 |
13.77
60.73 |
4.41 |
|
31. |
1 |
1
10 |
1
10 |
0.1
0.99 |
1
10 |
0.1
0.99 |
2.44
8.72 |
3.58 |
|
32. |
1 |
1 |
1
10 |
0.1
0.99 |
1
10 |
0.99
0.1 |
0.0011
0.0039 |
3.49 |
|
33. |
1 |
1 |
1 |
0.1
0.99 |
1
10 |
0.1
0.99 |
0.31
0.87 |
2.77 |
|
34. |
1
10 |
1
0.1 |
1 |
0.99 |
1 |
0.99 |
194.89
527.48 |
2.71 |
|
35. |
1 |
1 |
1 |
0.99 |
1 |
0.1
0.99 |
95.85
257.85 |
2.69 |
|
36. |
1 |
1 |
1
10 |
0.1
0.99 |
1
10 |
0.1
0.99 |
0.037
0.09 |
2.35 |
|
37. |
1 |
1
10 |
1
10 |
0.1
0.99 |
1
10 |
0.99 |
2.72
4.87 |
1.79 |
|
38. |
1 |
1
0.1 |
1
10 |
0.1
0.99 |
1
0.1 |
0.99 |
9.88
10.93 |
1.11 |
|
39. |
1 |
1 |
1
0.1 |
0.99
0.1 |
1
10 |
0.1
0.99 |
8.72
8.81 |
1.01 |
|
40. |
1 |
1
0.1 |
1
0.1 |
0.1
0.99 |
1
10 |
0.99 |
2.342
2.343 |
1.0 |
|
Table 2. The statistics of variable
parameters for Seuf /Seub, where Seuf /Seub ≥ 1 in descending order for groups |
||||||||
|
No.
in sequence |
Õ1 |
Õ2 |
Õ3 |
Õ4 |
Õ5 |
Õ6 |
Seub
Seuf. åä.2 (GDÐeub
GDÐeuf. $) |
Seuf / Seub (GDÐeuf / GDÐeub) |
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
1
variable |
||||||||
|
1. |
1 |
1
10 |
1 |
0.99 |
1 |
0.99 |
194.89
1.91Å+05
|
978.57 |
|
2. |
1
10 |
1 |
1 |
0.99 |
1 |
0.99 |
194.89
6034.81 |
30.97 |
|
3. |
1 |
1 |
1 |
0.99 |
1 |
0.1
0.99 |
95.85
257.85 |
2.69 |
|
2 variables |
||||||||
|
4. |
1
10 |
1
10 |
1
0.1 |
0.99
0.1 |
1 |
0.99 |
194.89
1.02Å+07 |
52231.12 |
|
5. |
1
10 |
1
10 |
1 |
0.99 |
1 |
0.99 |
194.89
6.03Å+06 |
30944.36 |
|
6. |
1 |
1 |
1
10 |
0.1
0.99 |
1
0.1 |
0.99
0.1 |
7.09
8871.41 |
1250.53 |
|
7. |
1 |
1 |
1
0.1 |
0.1
0.99 |
1
0.1 |
0.1
0.99 |
8.65
1467.03 |
169.68 |
|
8. |
1 |
1
10 |
1
0.1 |
0.1
0.99 |
1
0.1 |
0.99 |
13.77
2090.08 |
151.83 |
|
9. |
1
10 |
1
10 |
1
10 |
0.99
0.1 |
1 |
0.99 |
194.89
10183.31 |
52.25 |
|
10. |
1 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
41.74
1307.04 |
31.31 |
|
11. |
1
10 |
1 |
1
10 |
0.1
0.99 |
1
0.1 |
0.99 |
13.77
292.55 |
21.25 |
|
12. |
1
10 |
1
0.1 |
1
0.1 |
0.1
0.99 |
1 |
0.99 |
14.36
194.89 |
13.57 |
|
13. |
1 |
1
10 |
1
0.1 |
0.99
0.1 |
1
10 |
0.99 |
14.62
137.21 |
9.38 |
|
14. |
1
10 |
1
0.1 |
1
0.1 |
0.99 |
1 |
0.99 |
194.89
995.1 |
5.11 |
|
15. |
1 |
1 |
1
10 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
6.84
32.49 |
4.75 |
|
16. |
1 |
1 |
1
10 |
0.1
0.99 |
1
10 |
0.99
0.1 |
0.0011
0.0039 |
3.49 |
|
17. |
1 |
1 |
1
10 |
0.1
0.99 |
1
10 |
0.1
0.99 |
0.037
0.09 |
2.35 |
|
18. |
1 |
1
10 |
1
10 |
0.1
0.99 |
1
10 |
0.99 |
2.72
4.87 |
1.79 |
|
19. |
1 |
1
0.1 |
1
10 |
0.1
0.99 |
1
0.1 |
0.99 |
9.88
10.93 |
1.11 |
|
20. |
1 |
1 |
1
0.1 |
0.99
0.1 |
1
10 |
0.1
0.99 |
8.72
8.81 |
1.01 |
|
21. |
1 |
1
0.1 |
1
0.1 |
0.1
0.99 |
1
10 |
0.99 |
2.342
2.343 |
1.0 |
|
3 variables |
||||||||
|
22. |
1 |
1
10 |
1
0.1 |
0.1
0.99 |
1 |
0.99 |
14.36
1.91Å+05 |
13280.39 |
|
23. |
1
10 |
1
10 |
1
10 |
0.99 |
1 |
0.99 |
194.89
1.91Å+05 |
978.57 |
|
24. |
1
10 |
1 |
1
10 |
0.1
0.99 |
1 |
0.99 |
14.36
6034.81 |
420.24 |
|
25. |
1 |
1 |
1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
61.96
14973.34 |
241.67 |
|
26. |
1 |
1 |
1 |
0.1
0.99 |
1
0.1 |
0.1
0.99 |
8.65
519.37 |
60.07 |
|
27. |
1 |
1 |
1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
35.09
462.80 |
13.19 |
|
28. |
1 |
1 |
1 |
0.1
0.99 |
1
10 |
0.1
0.99 |
0.31
0.87 |
2.77 |
|
3 variables |
||||||||
|
29. |
1 |
1
10 |
1
0.1 |
0.99 |
1 |
0.99 |
194.89
6.03Å+06 |
30944.36 |
|
30. |
1 |
1 |
1 |
0.99 |
1
0.1 |
0.99
0.1 |
281.61
280504.87 |
996.10 |
|
31. |
1 |
1 |
1 |
0.99 |
1
0.1 |
0.1
0.99 |
142.99
7059.34 |
49.37 |
|
32. |
1 |
1
10 |
1
10 |
0.99 |
1 |
0.99 |
194.89
6034.81 |
30.97 |
|
33. |
1 |
1 |
1 |
0.1
0.99 |
1
0.1 |
0.99 |
13.77
60.73 |
4.41 |
|
34. |
1
10 |
1
0.1 |
1 |
0.99 |
1 |
0.99 |
194.89
527.48 |
2.71 |
|
4 variables |
||||||||
|
35. |
1 |
1
10 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
281.61
1.50Å+07 |
53166.38 |
|
36. |
1 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
79.16
4.73Å+05 |
5980.97 |
|
37. |
1 |
1
10 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
142.99
99734.86 |
697.47 |
|
38. |
1
10 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
177.83
6787.10 |
68.36 |
|
39. |
1 |
1
10 |
1
10 |
0.1
0.99 |
1
10 |
0.1
0.99 |
2.44
8.72 |
3.58 |
|
all the variables |
||||||||
|
40. |
1
10 |
1
0.1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
162.05
14973.34 |
92.40 |
|
Table 3. The statistics of variable
parameters for Seuf /Seub, where Seuf /Seub ≥ 1 and Õ2 = 1 in descending order
for groups |
||||||||
|
No.
in sequence |
Õ1 |
Õ2 |
Õ3 |
Õ4 |
Õ5 |
Õ6 |
Seub
Seuf. åä.2 (GDÐeub
GDÐeuf. $) |
Seuf / Seub (GDÐeuf / GDÐeub) |
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
|
1 variable |
||||||||
|
1.
|
1
10 |
1 |
1 |
0.99 |
1 |
0.99 |
194.89
6034.81 |
30.97 |
|
2.
|
1 |
1 |
1 |
0.99 |
1 |
0.1
0.99 |
95.85
257.85 |
2.69 |
|
2 variables |
||||||||
|
3.
|
1 |
1 |
1
10 |
0.1
0.99 |
1
0.1 |
0.99
0.1 |
7.09
8871.41 |
1250.53 |
|
4.
|
1 |
1 |
1
0.1 |
0.1
0.99 |
1
0.1 |
0.1
0.99 |
8.65
1467.03 |
169.68 |
|
5.
|
1 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
41.74
1307.04 |
31.31 |
|
6.
|
1
10 |
1 |
1
10 |
0.1
0.99 |
1
0.1 |
0.99 |
13.77
292.55 |
21.25 |
|
7.
|
1 |
1 |
1
10 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
6.84
32.49 |
4.75 |
|
8.
|
1 |
1 |
1
10 |
0.1
0.99 |
1
10 |
0.99
0.1 |
0.0011
0.0039 |
3.49 |
|
9.
|
1 |
1 |
1
10 |
0.1
0.99 |
1
10 |
0.1
0.99 |
0.037
0.09 |
2.35 |
|
10.
|
1 |
1 |
1
0.1 |
0.99
0.1 |
1
10 |
0.1
0.99 |
8.72
8.81 |
1.01 |
|
3 variables |
||||||||
|
11.
|
1
10 |
1 |
1
10 |
0.1
0.99 |
1 |
0.99 |
14.36
6034.81 |
420.24 |
|
12.
|
1 |
1 |
1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
61.96
14973.34 |
241.67 |
|
13.
|
1 |
1 |
1 |
0.1
0.99 |
1
0.1 |
0.1
0.99 |
8.65
519.37 |
60.07 |
|
14.
|
1 |
1 |
1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
35.09
462.80 |
13.19 |
|
15.
|
1 |
1 |
1 |
0.1
0.99 |
1
10 |
0.1
0.99 |
0.31
0.87 |
2.77 |
|
4 variables |
||||||||
|
16.
|
1 |
1 |
1 |
0.99 |
1
0.1 |
0.99
0.1 |
281.61
280504.87 |
996.10 |
|
17.
|
1 |
1 |
1 |
0.99 |
1
0.1 |
0.1
0.99 |
142.99
7059.34 |
49.37 |
|
18.
|
1 |
1 |
1 |
0.1
0.99 |
1
0.1 |
0.99 |
13.77
60.73 |
4.41 |
|
5 variables |
||||||||
|
19.
|
1 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.99
0.1 |
79.16
4.73Å+05 |
5980.97 |
|
20.
|
1
10 |
1 |
1
0.1 |
0.99
0.1 |
1
0.1 |
0.1
0.99 |
177.83
6787.10 |
68.36 |
REFERENCES
1.
Pil E. A. Use of the
shells' theory for purposes of description of processes taking place in economy
// Àëüìàíàõ ñîâðåìåííîé íàóêè è îáðàçîâàíèÿ (Almanac of modern science and
education). 2009. ¹3. P. 137-139
2.
Pil E. A. Influence of
different variables onto economic shell of the country // Àëüìàíàõ ñîâðåìåííîé íàóêè è îáðàçîâàíèÿ (Almanac of modern science and
education). 2012. ¹12 (67).
P. 123-126
3.
Pil E.A. Variants of
macroeconomics development after being affected by different forces //
Materials of the XII International scientific and practical conference,
«Prospect of world science - 2016», 30 July 7 August. 2016 Volume 2. Economic science. Governance.
4.
Pil E.A. Theory of the
financial crises // International Scientific and Practical Conference. Topical
researches of the world science (June 2021, 2015) Vol. IV Dubai, UAE. 2015
Ð. 4456